硬核機器學習幹貨,手把手教你寫KNN!
機器學習相關概念
人工智能、機器學習和深度學習的關系
在探討算法之前,我們先來談一談什麽是機器學習。相信大家都聽說過AlphaGo:2016年3月,AlphaGo與圍棋世界冠軍李世石進行圍棋人機大戰,最終以4:1獲勝;2017年5月,AlphaGo與世界圍棋冠軍柯潔對戰,以3:0獲勝。AlphaGo其實就是一款圍棋人工智能程序,其主要工作原理是“深度學習”。看一下下面這張圖,來了解一下,人工智能、機器學習和深度學習的關系。
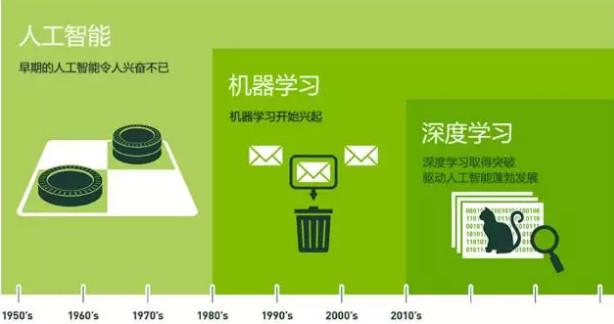
在20世紀五十年代,人工智能開始興起,早期的人工智能還是讓人興奮的(雖然後來發展歷程跌宕起伏,像下面這張圖,比過山車還刺激,當然這個不是我們今天的探討重點,感興趣的小夥伴們可以自行補充這塊知識)。在八十年代的時候,機器學習作為人工智能的一個分支也開始興起,之後也得到了很廣泛的應用,比如淘寶京東商品推送,豆瓣電影的“猜你喜歡”這類的推薦系統,還有其他的領域,像 數據挖掘、計算機視覺、自然語言處理、生物特征識別、搜索引擎、醫學診斷、檢測信用卡欺騙、語音與手寫識別、戰略遊戲、機器人等等等等,足以看出它的應用範圍有多廣。2010年左右,機器學習裏面的一個分支——深度學習取得了突破性進展,驅動人工智能蓬勃發展,比如像AlphaGo、人臉識別、圖像識別、文字識別、智能監控等等。
這裏我們重點來看一下,機器學習的概念,什麽是機器學習呢?他其實就是一段計算機程序,針對某一個特定的任務,從經驗中學習,並且變得越來越好。這就是機器學習。機器學習有哪些類型呢?主要就是監督學習、無監督學習、半監督學習、強化學習。
機器學習定義
人工智能(Artificial Intelligence, AI):是指由人工制造出來的系統所表現出來的智能。類似於電影中終結者、阿爾法狗這類的具有一定的和人類智慧同樣本質的一類智能的物體。
機器學習(Machine Learning, ML):是人工智能的一個分支,是實現人工智能的一個途徑,即以機器學習為手段解決人工智能中的問題。讓一個計算機程序針對某一個特定任務,從經驗中學習,並且越來越好
深度學習(Deep Learning, DL):是機器學習拉出的分支。是機器學習算法中的一種算法,一種實現機器學習的技術和學習方法。
機器學習類型
監督學習就是輸入一個包含有特征和目標的訓練集,並且要求目標是認為標註好的,也就是你需要提前告訴模型,特征是什麽,目標是什麽,然後讓模型根據訓練集學習出一個函數,那麽當新的數據來的時候,可以根據這個函數預測出結果。
無監督學習與監督學習唯一的不同就是訓練集沒有提前進行人為標註。
半監督學習顧名思義就是介於監督學習和無監督學習之間
強化學習就是通過觀察來學習做成某個動作,每個動作呢都會對環境有所影響,並且環境會給出反饋,學習對象就會根據觀察到的周圍環境的反饋來做出判斷。這個過程就是強化學習。

那我們今天要講的k-近鄰算法就屬於機器學習中的有監督學習,並且屬於有監督學習中的距離類模型。
一、k-近鄰算法是什麽
k-近鄰算法(k-Nearest Neighbour algorithm),又稱為KNN算法,是數據挖掘技術中原理最簡單的算法。KNN的工作原理:給定一個已知標簽類別的訓練數據集,輸入沒有標簽的新數據後,在訓練數據集中找到與新數據最鄰近的k個實例,如果這k個實例的多數屬於某個類別,那麽新數據就屬於這個類別。可以簡單理解為:由那些離X最近的k個點來投票決定X歸為哪一類。
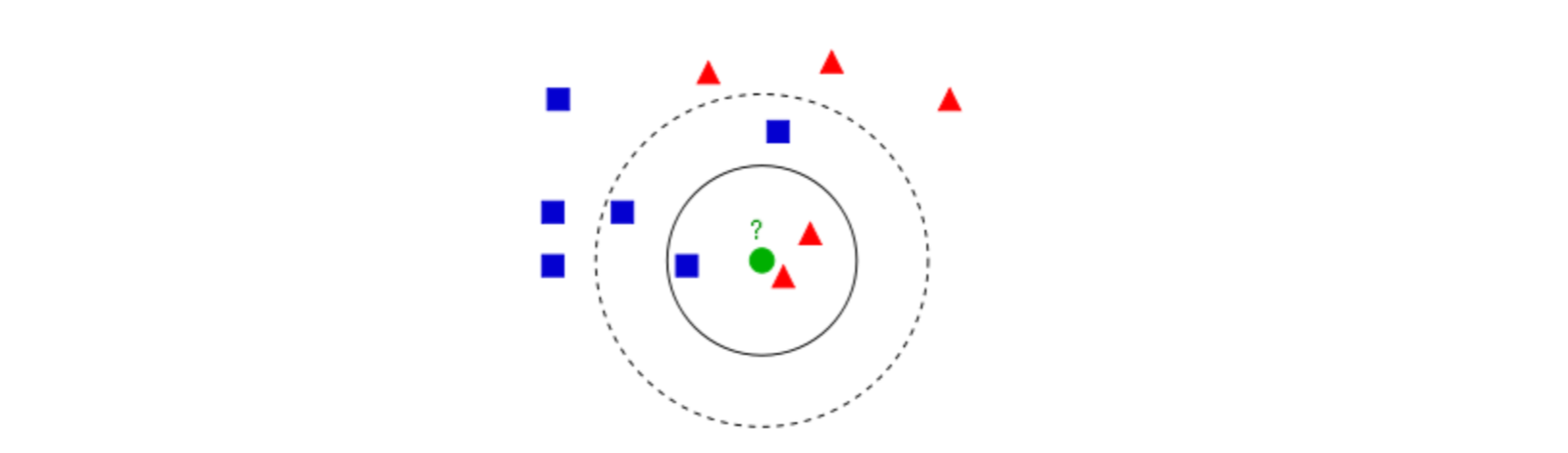
圖1
圖1中有紅色三角和藍色方塊兩種類別,我們現在需要判斷綠色圓點屬於哪種類別
當k=3時,綠色圓點屬於紅色三角這種類別;
當k=5時,綠色圓點屬於藍色方塊這種類別。
舉個簡單的例子,可以用k-近鄰算法分類一個電影是愛情片還是動作片。(打鬥鏡頭和接吻鏡頭數量為虛構)

表1 每部電影的打鬥鏡頭數、接吻鏡頭數和電影分類
表1就是我們已有的數據集合,也就是訓練樣本集。這個數據集有兩個特征——打鬥鏡頭數和接吻鏡頭數。除此之外,我們也知道每部電影的所屬類型,即分類標簽。粗略看來,接吻鏡頭多的就是愛情片,打鬥鏡頭多的就是動作片。以我們多年的經驗來看,這個分類還算合理。如果現在給我一部新的電影,告訴我電影中的打鬥鏡頭和接吻鏡頭分別是多少,那麽我可以根據你給出的信息進行判斷,這部電影是屬於愛情片還是動作片。而k-近鄰算法也可以像我們人一樣做到這一點。但是,這僅僅是兩個特征,如果把特征擴大到N個呢?我們人類還能憑經驗“一眼看出”電影的所屬類別嗎?想想就知道這是一個非常困難的事情,但算法可以,這就是算法的魅力所在。
我們已經知道k-近鄰算法的工作原理,根據特征比較,然後提取樣本集中特征最相似數據(最近鄰)的分類標簽。那麽如何進行比較呢?比如表1中新出的電影,我們該如何判斷他所屬的電影類別呢?如圖2所示。
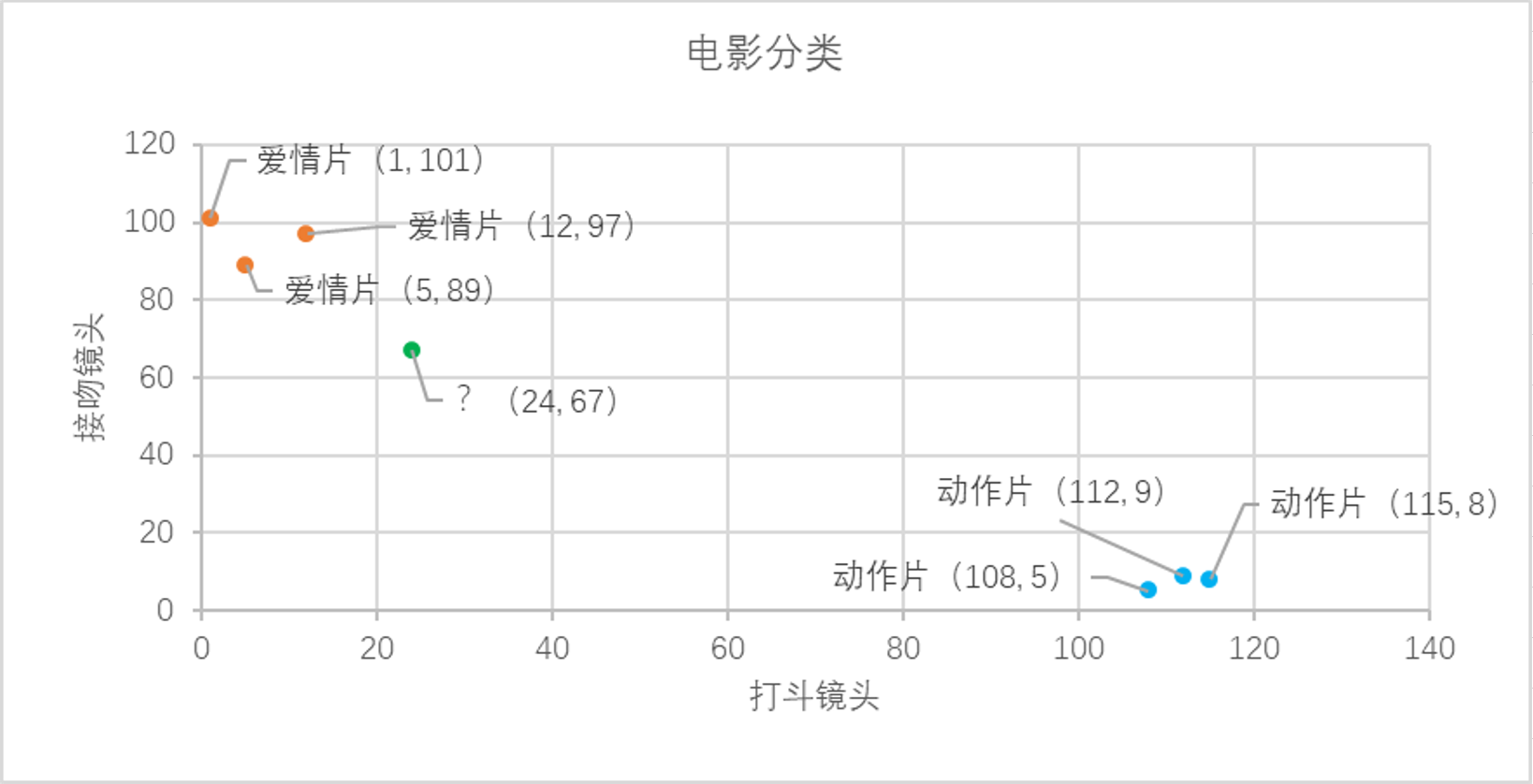
圖2 電影分類
我們可以從散點圖中大致推斷,這個未知電影有可能是愛情片,因為看起來距離已知的三個愛情片更近一點。k-近鄰算法是用什麽方法進行判斷呢?沒錯,就是距離度量。這個電影分類例子中有兩個特征,也就是在二維平面中計算兩點之間的距離,就可以用我們高中學過的距離計算公式:
如果是多個特征擴展到N維空間,怎麽計算?沒錯,我們可以使用歐氏距離(也稱歐幾裏得度量),如下所示

通過計算可以得到訓練集中所有電影與未知電影的距離,如表2所示

表2 與未知電影的距離計算結果
通過表2的計算結果,我們可以知道綠點標記的電影到愛情片《後來的我們》距離最近,為29.1。如果僅僅根據這個結果,判定綠點電影的類別為愛情片,這個算法叫做最近鄰算法,而非k-近鄰算法。k-近鄰算法步驟如下:
(1) 計算已知類別數據集中的點與當前點之間的距離;
(2) 按照距離遞增次序排序;
(3) 選取與當前點距離最小的k個點;
(4) 確定前k個點所在類別的出現頻率;
(5) 返回前k個點出現頻率最高的類別作為當前點的預測類別。
比如,現在K=4,那麽在這個電影例子中,把距離按照升序排列,距離綠點電影最近的前4個的電影分別是《後來的我們》、《前任3》、《無問西東》和《紅海行動》,這四部電影的類別統計為愛情片:動作片=3:1,出現頻率最高的類別為愛情片,所以在k=4時,綠點電影的類別為愛情片。這個判別過程就是k-近鄰算法。
二、k-近鄰算法的Python實現
在了解k-近鄰算法的原理及實施步驟之後,我們用python將這些過程實現。
1. 算法實現
1.構建已經分類好的原始數據集
為了方便驗證,這裏使用python的字典dict構建數據集,然後再將其轉化成DataFrame格式。
import pandas as pd ? rowdata={‘電影名稱‘:[‘無問西東‘,‘後來的我們‘,‘前任3‘,‘紅海行動‘,‘唐人街探案‘,‘戰狼2‘], ‘打鬥鏡頭‘:[1,5,12,108,112,115], ‘接吻鏡頭‘:[101,89,97,5,9,8], ‘電影類型‘:[‘愛情片‘,‘愛情片‘,‘愛情片‘,‘動作片‘,‘動作片‘,‘動作片‘]} movie_data= pd.DataFrame(rowdata) movie_data
2.計算已知類別數據集中的點與當前點之間的距離
new_data = [24,67] dist = list((((movie_data.iloc[:6,1:3]-new_data)**2).sum(1))**0.5) dist
3.將距離升序排列,然後選取距離最小的k個點
dist_l = pd.DataFrame({‘dist‘: dist, ‘labels‘: (movie_data.iloc[:6, 3])})
dr = dist_l.sort_values(by = ‘dist‘)[: 4]
dr
4.確定前k個點所在類別的出現頻率
re = dr.loc[:,‘labels‘].value_counts() re
5.選擇頻率最高的類別作為當前點的預測類別
result = []
result.append(re.index[0])
result
2. 封裝函數
完整的流程已經實現了,下面我們需要將這些步驟封裝成函數,方便我們後續的調用
import pandas as pd """ 函數功能:KNN分類器 參數說明: new_data:需要預測分類的數據集 dataSet:已知分類標簽的數據集(訓練集) k:k-近鄰算法參數,選擇距離最小的k個點 返回: result:分類結果 """ ? def classify0(inX,dataSet,k): result = [] dist = list((((dataSet.iloc[:,1:3]-inX)**2).sum(1))**0.5) dist_l = pd.DataFrame({‘dist‘:dist,‘labels‘:(dataSet.iloc[:, 3])}) dr = dist_l.sort_values(by = ‘dist‘)[: k] re = dr.loc[:, ‘labels‘].value_counts() result.append(re.index[0]) return result
測試函數運行結果
inX = new_data dataSet = movie_data k = 3 classify0(inX,dataSet,k)
這就是我們使用k-近鄰算法構建的一個分類器,根據我們的“經驗”可以看出,分類器給的答案還是比較符合我們的預期的。
學習到這裏,有人可能會問:”分類器何種情況下會出錯?“或者”分類器給出的答案是否永遠都正確?“答案一定是否定的,分類器並不會得到百分百正確的結果,我們可以使用很多種方法來驗證分類器的準確率。此外,分類器的性能也會受到很多因素的影響,比如k的取值就在很大程度上影響了分類器的預測結果,還有分類器的設置、原始數據集等等。為了測試分類器的效果,我們可以把原始數據集分為兩部分,一部分用來訓練算法(稱為訓練集),一部分用來測試算法的準確率(稱為測試集)。同時,我們不難發現,k-近鄰算法沒有進行數據的訓練,直接使用未知的數據與已知的數據進行比較,得到結果。因此,可以說,k-近鄰算法不具有顯式的學習過程。
三、k-近鄰算法之約會網站配對效果判定
海倫一直使用在線約會網站尋找適合自己的約會對象,盡管約會網站會推薦不同的人選,但她並不是每一個都喜歡,經過一番總結,她發現曾經交往的對象可以分為三類:
-
不喜歡的人
-
魅力一般的人
-
極具魅力得人
海倫收集約會數據已經有了一段時間,她把這些數據存放在文本文件datingTestSet.txt中,其中各字段分別為:
-
每年飛行常客裏程
-
玩遊戲視頻所占時間比
-
每周消費冰淇淋公升數
1. 準備數據
datingTest = pd.read_table(‘datingTestSet.txt‘,header=None) datingTest.head() datingTest.shape datingTest.info()
2. 分析數據
使用 Matplotlib 創建散點圖,查看各數據的分布情況
%matplotlib inline import matplotlib as mpl import matplotlib.pyplot as plt ? #把不同標簽用顏色區分 Colors = [] for i in range(datingTest.shape[0]): m = datingTest.iloc[i,-1] if m==‘didntLike‘: Colors.append(‘black‘) if m==‘smallDoses‘: Colors.append(‘orange‘) if m==‘largeDoses‘: Colors.append(‘red‘) ? #繪制兩兩特征之間的散點圖 plt.rcParams[‘font.sans-serif‘]=[‘Simhei‘] #圖中字體設置為黑體 pl=plt.figure(figsize=(12,8)) fig1=pl.add_subplot(221) plt.scatter(datingTest.iloc[:,1],datingTest.iloc[:,2],marker=‘.‘,c=Colors) plt.xlabel(‘玩遊戲視頻所占時間比‘) plt.ylabel(‘每周消費冰淇淋公升數‘) ? ? fig2=pl.add_subplot(222) plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,1],marker=‘.‘,c=Colors) plt.xlabel(‘每年飛行常客裏程‘) plt.ylabel(‘玩遊戲視頻所占時間比‘) ? fig3=pl.add_subplot(223) plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,2],marker=‘.‘,c=Colors) plt.xlabel(‘每年飛行常客裏程‘) plt.ylabel(‘每周消費冰淇淋公升數‘) plt.show()
3. 數據歸一化
下表是提取的4條樣本數據,如果我們想要計算樣本1和樣本2之間的距離,可以使用歐幾裏得計算公式:


表3 4條樣本數據
我們很容易發現,上面公式中差值最大的屬性對計算結果的影響最大,也就是說每年飛行常客裏程對計算結果的影響遠遠大於其他兩個特征,原因僅僅是因為它的數值比較大,但是在海倫看來這三個特征是同等重要的,所以接下來我們要進行數值歸一化的處理,使得這三個特征的權重相等。
數據歸一化的處理方法有很多種,比如0-1標準化、Z-score標準化、Sigmoid壓縮法等等,在這裏我們使用最簡單的0-1標準化,公式如下:

""" 函數功能:歸一化 參數說明: dataSet:原始數據集 返回:0-1標準化之後的數據集 """ ? def minmax(dataSet): minDf = dataSet.min() maxDf = dataSet.max() normSet = (dataSet - minDf )/(maxDf - minDf) return normSet
將我們的數據集帶入函數,進行歸一化處理
datingT = pd.concat([minmax(datingTest.iloc[:, :3]), datingTest.iloc[:,3]], axis=1)
datingT.head()
4. 劃分訓練集和測試集
前面概述部分我們有提到,為了測試分類器的效果,我們可以把原始數據集分為訓練集和測試集兩部分,訓練集用來訓練模型,測試集用來驗證模型準確率。
關於訓練集和測試集的切分函數,網上一搜一大堆,Scikit Learn官網上也有相應的函數比如model_selection 類中的train_test_split 函數也可以完成訓練集和測試集的切分。
通常來說,我們只提供已有數據的90%作為訓練樣本來訓練模型,其余10%的數據用來測試模型。這裏需要註意的10%的測試數據一定要是隨機選擇出來的,由於海倫提供的數據並沒有按照特定的目的來排序,所以我們這裏可以隨意選擇10%的數據而不影響其隨機性。
""" 函數功能:切分訓練集和測試集 參數說明: dataSet:原始數據集 rate:訓練集所占比例 返回:切分好的訓練集和測試集 """ ? def randSplit(dataSet,rate=0.9): n = dataSet.shape[0] m = int(n*rate) train = dataSet.iloc[:m,:] test = dataSet.iloc[m:,:] test.index = range(test.shape[0]) return train,test
train,test = randSplit(datingT)
train
test
5. 分類器針對於約會網站的測試代碼
接下來,我們一起來構建針對於這個約會網站數據的分類器,上面我們已經將原始數據集進行歸一化處理然後也切分了訓練集和測試集,所以我們的函數的輸入參數就可以是train、test和k(k-近鄰算法的參數,也就是選擇的距離最小的k個點)。
""" 函數功能:k-近鄰算法分類器 參數說明: train:訓練集 test:測試集 k:k-近鄰參數,即選擇距離最小的k個點 返回:預測好分類的測試集 """ ? def datingClass(train,test,k): n = train.shape[1] - 1 m = test.shape[0] result = [] for i in range(m): dist = list((((train.iloc[:, :n] - test.iloc[i, :n]) ** 2).sum(1))**0.5) dist_l = pd.DataFrame({‘dist‘: dist, ‘labels‘: (train.iloc[:, n])}) dr = dist_l.sort_values(by = ‘dist‘)[: k] re = dr.loc[:, ‘labels‘].value_counts() result.append(re.index[0]) result = pd.Series(result) test[‘predict‘] = result acc = (test.iloc[:,-1]==test.iloc[:,-2]).mean() print(f‘模型預測準確率為{acc}‘) return test
最後,測試上述代碼能否正常運行,使用上面生成的測試集和訓練集來導入分類器函數之中,然後執行並查看分類結果。
datingClass(train,test,5)
從結果可以看出,我們模型的準確率還不錯,這是一個不錯的結果了。
四、算法總結
1. 優點
-
簡單好用,容易理解,精度高,理論成熟,既可以用來做分類也可以用來做回歸
-
可用於數值型數據和離散型數據
-
無數據輸入假定
-
適合對稀有事件進行分類
2. 缺點
-
計算復雜性高;空間復雜性高;
-
計算量太大,所以一般數值很大的時候不用這個,但是單個樣本又不能太少,否則容易發生誤分。
-
樣本不平衡問題(即有些類別的樣本數量很多,而其它樣本的數量很少)
-
可理解性比較差,無法給出數據的內在含義
其他
-
公開課視頻:https://space.bilibili.com/108044200
硬核機器學習幹貨,手把手教你寫KNN!

