藍橋杯——九宮重排、青蛙跳杯子
阿新 • • 發佈:2019-03-17
快速 藍橋 一行 har nod lose file 至少 發現
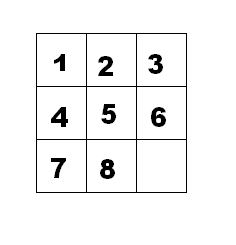
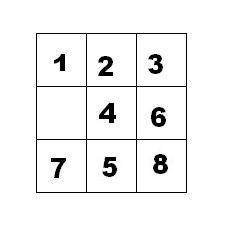
我們把第一個圖的局面記為:12345678.
把第二個圖的局面記為:123.46758
顯然是按從上到下,從左到右的順序記錄數字,空格記為句點。
本題目的任務是已知九宮的初態和終態,求最少經過多少步的移動可以到達。如果無論多少步都無法到達,則輸出-1。 輸入格式 輸入第一行包含九宮的初態,第二行包含九宮的終態。 輸出格式 輸出最少的步數,如果不存在方案,則輸出-1。 樣例輸入 12345678.
46758123. 樣例輸出 22 思考過程: 
X星球的居民喜歡把它們放在一排茶杯裏,這樣可以觀察它們跳來跳去。
如下圖,有一排杯子,左邊的一個是空著的,右邊的杯子,每個裏邊有一只青蛙。
*WWWBBB
其中,W字母表示白色青蛙,B表示黑色青蛙,*表示空杯子。
X星的青蛙很有些癖好,它們只做3個動作之一:
1. 跳到相鄰的空杯子裏。
2. 隔著1只其它的青蛙(隨便什麽顏色)跳到空杯子裏。
3. 隔著2只其它的青蛙(隨便什麽顏色)跳到空杯子裏。
對於上圖的局面,只要1步,就可跳成下圖局面:
WWW*BBB
本題的任務就是已知初始局面,詢問至少需要幾步,才能跳成另一個目標局面。
輸入為2行,2個串,表示初始局面和目標局面。
輸出要求為一個整數,表示至少需要多少步的青蛙跳。 樣例輸入 *WWBB
WWBB* 樣例輸出 2 樣例輸入 WWW*BBB
BBB*WWW 樣例輸出 10 數據規模和約定 我們約定,輸入的串的長度不超過15 思路:和九宮重排一模一樣,在九宮重排(60分代碼)的代碼上稍作改動,
1.歷屆試題 九宮重排
時間限制:1.0s 內存限制:256.0MB 問題描述 如下面第一個圖的九宮格中,放著 1~8 的數字卡片,還有一個格子空著。與空格子相鄰的格子中的卡片可以移動到空格中。經過若幹次移動,可以形成第二個圖所示的局面。我們把第一個圖的局面記為:12345678.
把第二個圖的局面記為:123.46758
顯然是按從上到下,從左到右的順序記錄數字,空格記為句點。
本題目的任務是已知九宮的初態和終態,求最少經過多少步的移動可以到達。如果無論多少步都無法到達,則輸出-1。 輸入格式 輸入第一行包含九宮的初態,第二行包含九宮的終態。 輸出格式 輸出最少的步數,如果不存在方案,則輸出-1。 樣例輸入 12345678.
46758123. 樣例輸出 22 思考過程:
九宮格數字的移動,其實是由空格移動造成的,所以,站在空格的角度上,將空格當作運動的點,有四種運動方向:前後左右。以前迷宮問題, 就是起點走到終點,深度搜索(隊列),最先到達終點時的步數,就是最短路徑;九宮重排問題一樣,用字符串表示九宮格的狀態,遍歷的過程中,當 到達的狀態和目標狀態一致時結束,但是怎麽避免老是走重復的路呢(排重)?那就需要將過程中的狀態全部記錄下來,每走到新的狀態,比較一下先前是否出現過,若出現過,就停止走這條路,即不讓這一狀態入隊列即可。將先前的狀態放入set容器可以很快速知道是否出現過。
第一次 TLE 運行超時了,60分;
第二次 TLE 運行超時了,80分, 將操作(1)、(2)交換位置,要986ms,說明沒有在根源上減少時間。
第三次,100昏,將結構體增加‘.‘(空格)的坐標,省去每次找坐標的時間。
<c++代碼>

1 #include<stdio.h> 2 #include<set> 3 #include<queue> 4 #include<string.h> 5 #include<string> 6 using namespace std; 7View Codestruct node 8 { 9 int step,pos_x,pos_y; 10 char str[15]; 11 }; 12 char str1[15],str2[15];//初始狀態、目標狀態 13 int D[4][2]= {-1,0,1,0,0,-1,0,1}; 14 set<string> Set;//定義一個string類型的set容器,存放九宮格的狀態 15 queue<node> que;//定義一個隊列,存放行走過程中的狀態,每一個node包含達到此狀態的步數step、和當時的狀態 16 int blank_pos(char *str) //空格的位置 17 { 18 int l=strlen(str); 19 for(int i=0; i<l; i++) 20 { 21 if(str[i]==‘.‘) 22 return i; 23 } 24 } 25 int bfs() 26 { 27 char next_str[15]; 28 node n,new_node; 29 int pos,pos_x,pos_y,next_x,next_y,next_pos; 30 while(!que.empty()) 31 { 32 n=que.front();//隊首出隊 33 que.pop(); 34 for(int i=0; i<4; i++) //空格往四個方向行走 35 { 36 strcpy(next_str,n.str);//將來next_str要在n.str的基礎上改動,但是n.str一直不能動,因為是四個方向共用的 37 next_x=n.pos_x+D[i][0]; 38 next_y=n.pos_y+D[i][1]; 39 if(next_x>=0&&next_x<=2&&next_y>=0&&next_y<=2) //將要走的那一步符合要求 40 { 41 //將接下來的狀態表示出來(空格上的’0‘ 變為 (next_x,next_y)上的字符,(next_x,next_y)變成空格;查看set裏是否有這個狀態,若有就不走這一步,避免重復) 42 pos=n.pos_x*3+n.pos_y; 43 next_pos=next_x*3+next_y;//新空格位置 44 next_str[next_pos]=‘.‘; 45 next_str[pos]=n.str[next_pos]; 46 //判重 47 if(Set.find(next_str)==Set.end()) //表示沒有找到重的 48 { 49 new_node.step=n.step+1; 50 //(1)查看著個狀態是不是目標狀態 51 if(!strcmp(next_str,str2)) //即得到了目標狀態 52 { 53 return new_node.step; 54 } 55 //(2)將新的狀態記錄在隊列和Set裏 56 strcpy(new_node.str,next_str); 57 new_node.pos_x=next_x; 58 new_node.pos_y=next_y; 59 que.push(new_node); 60 Set.insert(next_str); 61 } 62 } 63 } 64 } 65 return -1; 66 } 67 int main() 68 { 69 //輸入 70 node n; 71 int min,pos; 72 scanf("%s",str1); 73 scanf("%s",str2);//目標 74 if(!strcmp(str1,str2)) //即得到了目標狀態 75 { 76 printf("%d",0); 77 } 78 else 79 { 80 //初始狀態放入隊列和set容器 81 pos=blank_pos(str1);//找‘.‘的位置 82 n.pos_x=pos/3; 83 n.pos_y=pos%3; 84 n.step=0; 85 strcpy(n.str,str1); 86 que.push(n); 87 Set.insert(n.str); 88 min=bfs();//廣搜,找出最少步驟 89 printf("%d",min); 90 } 91 return 0; 92 }
2.歷屆試題 青蛙跳杯子
時間限制:1.0s 內存限制:256.0MB 問題描述 X星球的流行寵物是青蛙,一般有兩種顏色:白色和黑色。X星球的居民喜歡把它們放在一排茶杯裏,這樣可以觀察它們跳來跳去。
如下圖,有一排杯子,左邊的一個是空著的,右邊的杯子,每個裏邊有一只青蛙。
*WWWBBB
其中,W字母表示白色青蛙,B表示黑色青蛙,*表示空杯子。
X星的青蛙很有些癖好,它們只做3個動作之一:
1. 跳到相鄰的空杯子裏。
2. 隔著1只其它的青蛙(隨便什麽顏色)跳到空杯子裏。
3. 隔著2只其它的青蛙(隨便什麽顏色)跳到空杯子裏。
對於上圖的局面,只要1步,就可跳成下圖局面:
WWW*BBB
本題的任務就是已知初始局面,詢問至少需要幾步,才能跳成另一個目標局面。
輸入為2行,2個串,表示初始局面和目標局面。
輸出要求為一個整數,表示至少需要多少步的青蛙跳。 樣例輸入 *WWBB
WWBB* 樣例輸出 2 樣例輸入 WWW*BBB
BBB*WWW 樣例輸出 10 數據規模和約定 我們約定,輸入的串的長度不超過15 思路:和九宮重排一模一樣,在九宮重排(60分代碼)的代碼上稍作改動,
青蛙跳杯子,感覺和九宮重排很相似,雖然是青蛙在跳,但是可以看成空杯子在跳,有6種跳法:往左一個、往右一個,往左兩個、往右兩個,往左三個、往右三個。誒等一下!!會不會不只一個空杯子?、這樣就不行了,不管了,就先當所有案例的都只有一個空杯子,兩個的話,就2*6種跳法?後來提交代碼後,發現只用考慮一個空杯子。
<c++代碼>

1 include<stdio.h> 2 #include<set> 3 #include<string> 4 #include<string.h> 5 #include<queue> 6 using namespace std; 7 struct node{ 8 int step; 9 char str[20]; 10 }; 11 int D[6]={-1,1,-2,2,-3,3}; 12 int len;//杯子個數 13 char str1[20],str2[20];//初始狀態、目標狀態 14 set<string> Set;//用Set存放跳的過程中的狀態 15 queue<node> que;//node每一次跳躍之後的狀態和已經跳躍的步數 16 int blank_pos(char *str) //空格的位置 17 { 18 for(int i=0; i<strlen(str); i++) 19 { 20 if(str[i]==‘*‘) 21 return i; 22 } 23 } 24 int bfs() 25 { 26 char next_str[20]; 27 node n,new_node; 28 int pos,next_pos; 29 while(!que.empty()) 30 { 31 n=que.front();//隊首出隊 32 //printf("%s\n",n.str); 33 que.pop(); 34 //得出‘*‘的位置 35 pos=blank_pos(n.str); 36 for(int i=0; i<6; i++) //*有五種跳法 37 { 38 strcpy(next_str,n.str);//將來next_str要在n.str的基礎上改動,但是n.str一直不能動,因為是四個方向共用的 39 next_pos=pos+D[i]; 40 if(next_pos>=0&&next_pos<len) //將要走的那一步符合要求 41 { 42 //將接下來的狀態表示出來(‘*‘變為 next_pos上的字符,next_pos上的字符變成‘*‘;查看set裏是否有這個狀態,若有就不走這一步,避免重復) 43 44 next_str[next_pos]=‘*‘; 45 next_str[pos]=n.str[next_pos]; 46 //判重 47 if(Set.find(next_str)==Set.end()) //表示沒有找到重的 48 { 49 //將新的狀態記錄在隊列和Set裏 50 strcpy(new_node.str,next_str); 51 new_node.step=n.step+1; 52 que.push(new_node); 53 Set.insert(next_str); 54 //查看著個狀態是不是目標狀態 55 if(!strcmp(next_str,str2)) //即得到了目標狀態 56 { 57 return new_node.step; 58 } 59 } 60 } 61 } 62 } 63 return -1; 64 } 65 int main(){ 66 node n; 67 int min; 68 scanf("%s",str1); 69 scanf("%s",str2);//目標 70 len=strlen(str1); 71 if(!strcmp(str1,str2)) //即得到了目標狀態 72 { 73 printf("%d",0); 74 } 75 else 76 { 77 //初始狀態放入隊列和set容器 78 n.step=0; 79 strcpy(n.str,str1); 80 que.push(n); 81 Set.insert(n.str); 82 min=bfs();//廣搜,找出最少步驟 83 printf("%d",min); 84 } 85 return 0; 86 }View Code
藍橋杯——九宮重排、青蛙跳杯子

