開發十年，就只剩下這套架構體系了！ >>>   

N-最短路徑 是中科院分詞工具NLPIR進行分詞用到的一個重要演算法，張華平、劉群老師在論文《基於N-最短路徑方法的中文詞語粗分模型》中做了比較詳細的介紹。該演算法演算法基本思想很簡單，就是給定一待處理字串，根據詞典，找出詞典中所有可能的詞，構造出字串的一個有向無環圖，算出從開始到結束所有路徑中最短的前N條路徑。因為允許相等長度的路徑並列，故最終的結果集合會大於或等於N。

根據演算法思想，當我們拿到一個字串後，首先構造圖，接著針對圖計算最短路徑。下面以一個例子“他說的確實在理”進行說明，開始為了能夠簡單說明，首先假設圖上的邊權值均為1。 

先給出對這句話的3-最短路(即路徑最短的前3名, 因為有並列成分, 所以可能候選路徑大於3)徑求解過程圖： 

從節點4開始, 因為4是第一個出現多個前驅節點的

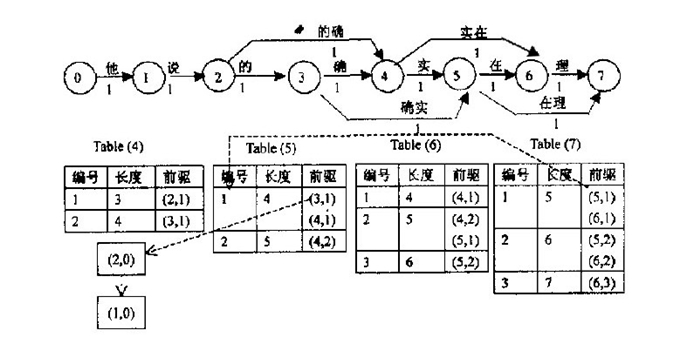
首先看圖中上方，它是根據一個已有詞典構造出的有向無環圖。它將字串分為單個的字，每個字用圖中相鄰的兩個結點表示，故對於長度為n的字串，需要n+1個結點。兩節點間若有邊，則表示兩節點間所包含的所有結點構成的詞，如圖中結點2、3、4構成詞“的確”。

圖構造出來後，接下來就要計算最短路徑，N-最短路徑是基於Dijkstra演算法的一種簡單擴充套件，它在每個結點處記錄了N個最短路徑值與該結點的前驅，具體過程如上圖中下方列表。Table(4)表示位於結點4時的最短路徑情況，表示從結點0到4有兩條路徑，長度為3的路徑前驅為2；長度為4的路徑前驅為3。前驅括號裡面第二個數表示對相同前驅結點的區分，如（4,1）、（4,2）。由列表可知，該字串的3-最短路徑結果集合為｛5,5,6,6,7｝。

當然，在實際情況中，權值不可能都設為1的，否則隨著字串長度n和最短路徑N的增大，長度相同的路徑數將會急劇增加。為了解決這樣的問題，我們需要通過某種策略為有向圖的邊賦權重，很自然的想法就是邊的權重就是該詞出現的可能性。

NShortPath的基本思想是Dijkstra演算法的變種，拿1-最短路來說吧，先Dijkstra求一次最短路，然後沿著最短路的路徑走下去，只不過在走到某個節點的時候，檢查到該節點在路徑上的下一個節點是否還有別的路到它（從PreNode查），如果有，就走這些別的路中的沒走過第一條（它們都是最短路上的途徑節點）。然後推廣到N-最短路，N-最短路中PreNode有N個，分別對應n-最短路時候的PreNode，就這麼簡單。

圖解

再談PreNode的準備

需要為每個頂點維護一個最小堆，最小堆裡儲存的是邊的花費，每條邊的終點是這個頂點。還需要維護到每個頂點的前N個最小路徑的花費：

回憶一下Dijkstra求最短路的時候，我們只需記錄一個最短路的累計花費就行了

這與此處的N-最短路徑顯著不同。

在遍歷圖的時候，與Dijkstra最短路徑不同，N-最短路徑從第二個節點開始，需要將當前節點可能到達的邊根據累積第i短長度+該邊的長度之和排序記錄到PreNode佇列陣列中，排序由CQueue完成的。

然後從CQueue出隊，這樣路徑長度就是升序了，按順序更新 weightArray[當前節點][第幾短路]就行了。

另外CQueue是一個不同於普通佇列的佇列，它維護了一個當前指標（下圖的藍色部分），這個藍色指標在求解第i短路徑的時候會用到。

假定看到這裡，演算法已經計算出了正確的PreNode佇列，下面討論如何從PreNode中找出N最短路徑的確切途經節點集合。

1-最短路徑的求解

整個計算過程維護了一個路徑棧，對於上圖來說，

1）首先將最後一個元素壓入棧（本例中是6號結點），什麼時候這個元素彈出棧，什麼時候整個任務結束。

2）對於每個結點的PreNode佇列，維護了一個當前指標，初始狀態都指向PreNode佇列中第一個元素。這個指標是由CQueue維護的，嚴格來講不屬於演算法關心的問題。

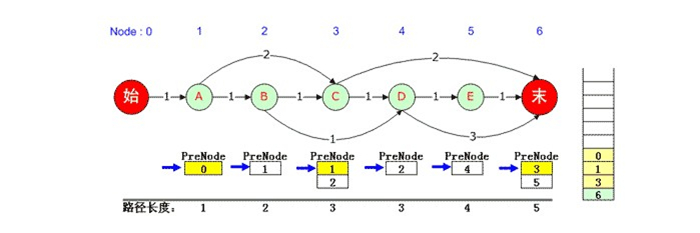
3）從右向左依次取出PreNode佇列中的當前元素（當前元素出隊）並壓入棧，並將佇列指標重新指向佇列中第一個元素。如上圖：6號元素PreNode是3，3號元素PreNode是1，1號元素PreNode是0。

4）當第一個元素壓入棧後，輸出棧內容即為一條佇列。本例中0, 1, 3, 6便是一條最短路徑。

5）將棧中的內容依次彈出，每彈出一個元素，就將當時壓棧時該元素對應的PreNode佇列指標下移一格。如果到了末尾無法下移，則繼續執行第5步（也就是繼續出棧），如果仍然可以移動，則執行第3步。

對於本例，先將“0”彈出棧，在路徑上0的下一個是1，得出該元素對應的是1號“A”結點的PreNode佇列，該佇列的當前指標已經無法下移，因此繼續彈出棧中的“1” ；同理該元素對應3號“C”結點，因此將3號“C”結點對應的PreNode佇列指標下移。由於可以移動，因此將佇列中的2壓入佇列，2號“B”結點的PreNode是1，因此再壓入1，依次類推，直到0被壓入，此時又得到了一條最短路徑，那就是0，1，2，3，6。如下圖：

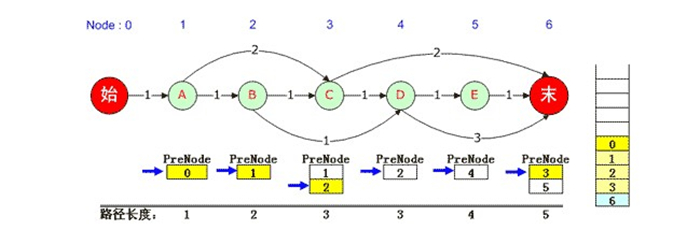
再往下，0、1、2都被彈出棧，3被彈出棧後，由於它對應的6號元素PreNode佇列記錄指標仍然可以下移，因此將5壓入堆疊並依次將其PreNode入棧，直到0被入棧。此時輸出第3條最短路徑：0, 1, 2, 4, 5, 6。如下圖：

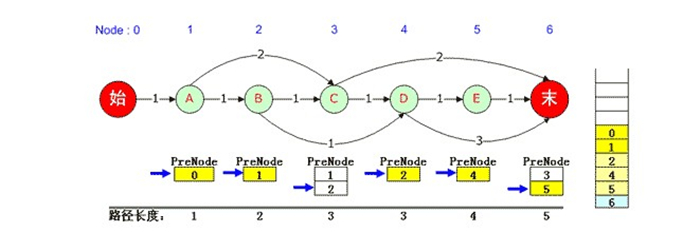
輸出完成後，緊接著又是出棧，此時已經沒有任何棧元素對應的PreNode佇列指標可以下移，於是堆疊中的最後一個元素6也被彈出棧，此時輸出工作完全結束。我們得到了3條最短路徑，分別是：

0, 1, 3, 6,

0, 1, 2, 3, 6,

0, 1, 2, 4, 5, 6,

推廣到N-最短路

N-最短路中PreNode有N個，分別對應n-最短路時候的PreNode，也就是當前路徑是第n短的時候，當前節點對應的PreNode佇列。

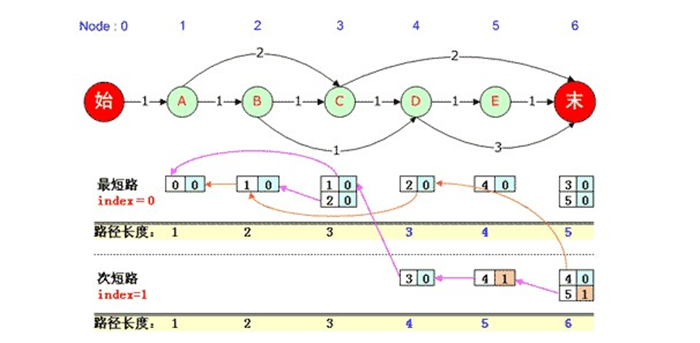
在該圖中，觀察黃顏色的路徑長度表格，到達1號、2號、3號結點的路徑雖然有多條，但長度只有一種長度，但到達4號“D”結點的路徑長度有兩種，即長度可能是3也可能是4，此時在“最短路”處（index＝0）記錄長度為3時的PreNode，在“次短路”處（index＝1）處記錄長度為4時的PreNode，依此類推。

值得注意的是，此時用來記錄PreNode的座標已經由前文求“1-最短路徑”時的一個數（ParentNode值)變為2個數（ParentNode值以及index值）。

如上圖所示，到達6號“末”結點的次短路徑有兩個ParentNode，一個是index=0中的4號結點，一個是index=1的5號結點，它們都使得總路徑長度為6。

當N=2時，我們求得了2-最短路徑，路徑長度有兩種，分別長度為5和6，而路徑總共有6條，如下：

最短路徑：

0, 1, 3, 6,

0, 1, 2, 3, 6,

0, 1, 2, 4, 5, 6,

========================

次短路徑

0, 1, 2, 4, 6,

0, 1, 3, 4, 5, 6,

0, 1, 2, 3, 4, 5, 6,

---------------------

相關推薦