線性代數的動態觀-線性變換(一)
阿新 • • 發佈:2019-04-25
n個向量組可以當作一個整體來看即矩陣,此時線性代數的靜態觀-向量空間中提到的座標向量可以寫成A.x=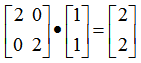 ,矩陣A可以看成一個作用力在標準正交基
,矩陣A可以看成一個作用力在標準正交基![]() 下將向量
下將向量![]() 移到向量
移到向量![]() 的位置上。
的位置上。
類似於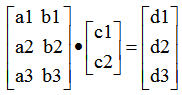 從線性組合的靜態觀比較好理解,但如果從動態觀來看就是把一個二維中的點移到三維空間中(這是一種升維但感覺不是很直觀)
從線性組合的靜態觀比較好理解,但如果從動態觀來看就是把一個二維中的點移到三維空間中(這是一種升維但感覺不是很直觀)
類似於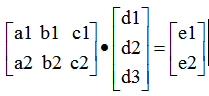 從線性組合的靜態觀不是很好理解,但如果從動態觀來看就是把一個三維中的點移到二維空間中(這是一種降維比如投影,日常生活中將物體通過燈光對映到牆面上就是投影)
從線性組合的靜態觀不是很好理解,但如果從動態觀來看就是把一個三維中的點移到二維空間中(這是一種降維比如投影,日常生活中將物體通過燈光對映到牆面上就是投影)
在進一步討論前需理解基的變換:
設基A=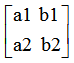 ,基B=
,基B=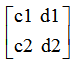 ,由於
,由於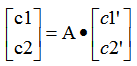 ,
,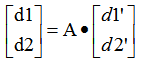 因此
因此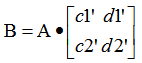 簡寫成B=A.P,這個P叫做基的變換矩陣。
簡寫成B=A.P,這個P叫做基的變換矩陣。
給定向量X,X=A.X1',X=B.X2',則A.X1'=B.X2',可進一步寫成A.X1'=A.P.X2',得到X1‘=P.X2'或X2’=![]()
