[開發技巧]·Python實現訊號濾波(基於scipy)
[開發技巧]·Python實現訊號濾波(基於scipy)
個人網站--> http://www.yansongsong.cn
GitHub主頁--> https://github.com/xiaosongshine

1.背景介紹
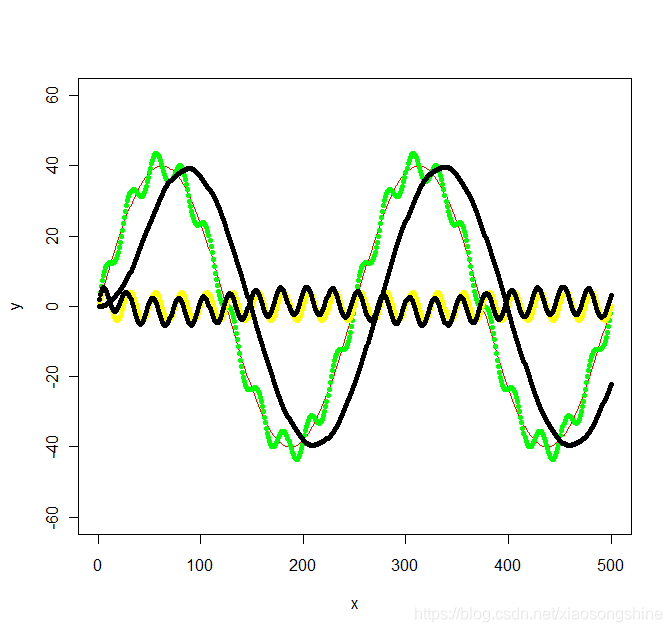
在深度學習中,有時會使用Matlab進行濾波處理,再將處理過的資料送入神經網路中。這樣是一般的處理方法,但是處理起來卻有些繁瑣,並且有時系統難以執行Matlab。Python作為一種十分強大的語言,是支援訊號濾波濾波處理的。
本文將以實戰的形式基於scipy模組使用Python實現簡單濾波處理,包括內容有1.低通濾波,2.高通濾波,3.帶通濾波,4.帶阻濾波器。具體的含義大家可以查閱大學課程,訊號與系統。簡單的理解就是低通濾波指的是去除高於某一閾值頻率的訊號;高通濾波去除低於某一頻率的訊號;帶通濾波指的是類似低通高通的結合保留中間頻率訊號;帶阻濾波也是低通高通的結合只是過濾掉的是中間部分。上面所說的內容會在實戰部分加以介紹,可以對比理解一下。
如何實現的呢?我的理解,是通過時域轉換為頻域,在頻域訊號中去除相應頻域訊號,最後在逆轉換還原為時域型號。具體的內容還是要查閱大學課程,訊號與系統。自己學的很一般就不班門弄斧了。
有什麼作用呢?My Opinions,可以消除一些干擾訊號,以低通濾波為例,例如我們如果只是統計脈搏訊號波形,應該在1Hz左右,卻發現波形訊號上有很多噪音,這些噪音都是成百上千Hz的,這些對於脈搏訊號波形就屬於無用的噪音,我們就可以通過低通濾波器將超出某一閾值的訊號過濾掉,此時得到的波形就會比較平滑了。
2.實戰演練
首先我們使用到了scipy模組,可以通過下述命令進行安裝:(我使用的Python==3.6)
pip install scipy
1).低通濾波
這裡假設取樣頻率為1000hz,訊號本身最大的頻率為500hz,要濾除400hz以上頻率成分,即截至頻率為400hz,則wn=2*400/1000=0.8。Wn=0.8
from scipy import signal b, a = signal.butter(8, 0.8, 'lowpass') #配置濾波器 8 表示濾波器的階數 filtedData = signal.filtfilt(b, a, data) #data為要過濾的訊號
2).低通濾波
這裡假設取樣頻率為1000hz,訊號本身最大的頻率為500hz,要濾除100hz以下頻率成分,即截至頻率為100hz,則wn=2*100/1000=0.2。Wn=0.2
from scipy import signal b, a = signal.butter(8, 0.2, 'highpass') #配置濾波器 8 表示濾波器的階數 filtedData = signal.filtfilt(b, a, data) #data為要過濾的訊號
3).帶通濾波
這裡假設取樣頻率為1000hz,訊號本身最大的頻率為500hz,要濾除100hz以下,400hz以上頻率成分,即截至頻率為100,400hz,則wn1=2*100/1000=0.2,Wn1=0.2; wn2=2*400/1000=0.8,Wn2=0.8。Wn=[0.02,0.8]
from scipy import signal b, a = signal.butter(8, [0.2,0.8], 'bandpass') #配置濾波器 8 表示濾波器的階數 filtedData = signal.filtfilt(b, a, data) #data為要過濾的訊號
4).帶阻濾波
這裡假設取樣頻率為1000hz,訊號本身最大的頻率為500hz,要濾除100hz以上,400hz以下頻率成分,即截至頻率為100,400hz,則wn1=2*100/1000=0.2,Wn1=0.2; wn2=2*400/1000=0.8,Wn2=0.8。Wn=[0.02,0.8],和帶通相似,但是帶通是保留中間,而帶阻是去除。
from scipy import signal b, a = signal.butter(8, [0.2,0.8], 'bandstop') #配置濾波器 8 表示濾波器的階數 filtedData = signal.filtfilt(b, a, data) #data為要過濾的訊號
3.函式介紹
1.函式的介紹
(1).濾波函式
scipy.signal.filtfilt(b, a, x, axis=-1, padtype='odd', padlen=None, method='pad', irlen=None)
輸入引數:
b: 濾波器的分子係數向量
a: 濾波器的分母系數向量
x: 要過濾的資料陣列。(array型)
axis: 指定要過濾的資料陣列x的軸
padtype: 必須是“奇數”、“偶數”、“常數”或“無”。這決定了用於過濾器應用的填充訊號的擴充套件型別。{‘odd’, ‘even’, ‘constant’, None}
padlen:在應用濾波器之前在軸兩端延伸X的元素數目。此值必須小於要濾波元素個數- 1。(int型或None)
method:確定處理訊號邊緣的方法。當method為“pad”時,填充訊號;填充型別padtype和padlen決定,irlen被忽略。當method為“gust”時,使用古斯塔夫森方法,而忽略padtype和padlen。{“pad” ,“gust”}
irlen:當method為“gust”時,irlen指定濾波器的脈衝響應的長度。如果irlen是None,則脈衝響應的任何部分都被忽略。對於長訊號,指定irlen可以顯著改善濾波器的效能。(int型或None)
輸出引數:
y:濾波後的資料陣列
(2).濾波器建構函式(僅介紹Butterworth濾波器)
scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba')
輸入引數:
N:濾波器的階數
Wn:歸一化截止頻率。計算公式Wn=2*截止頻率/取樣頻率。(注意:根據取樣定理,取樣頻率要大於兩倍的訊號本身最大的頻率,才能還原訊號。截止頻率一定小於訊號本身最大的頻率,所以Wn一定在0和1之間)。當構造帶通濾波器或者帶阻濾波器時,Wn為長度為2的列表。
btype : 濾波器型別{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’},
output : 輸出型別{‘ba’, ‘zpk’, ‘sos’},
輸出引數:
b,a: IIR濾波器的分子(b)和分母(a)多項式係數向量。output='ba'
z,p,k: IIR濾波器傳遞函式的零點、極點和系統增益. output= 'zpk'
sos: IIR濾波器的二階截面表示。output= 'sos'
4.參考
https://blog.csdn.net/weixin_37996604/article/details/82864680
https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.signal.filtfilt.html
https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.signal.butter.html#scipy.signal.butter
