nta remember ext 左右 rectangle define b- pri become

Largest Rectangle in a Histogram

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 26267 Accepted Submission(s): 8279


Problem Description A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

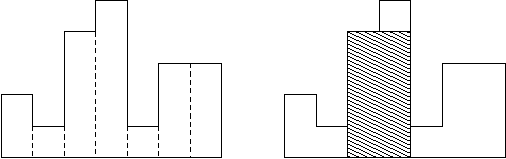
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Input The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.
Output For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.
Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

Source University of Ulm Local Contest 2003
Recommend LL
Statistic | Submit | Discuss | Note

給你一個直方圖，告訴你各個條形矩形的高度，求基線對齊構成的矩形中面積最大的矩形的面積對於每一個矩形。面積 = h[i]*(j-k+1),其中j，k是左右邊界，h[i]是矩形的高。並且對於j <= x <= k，h[i] <= h[x]。

分析

我們只需要求出每條矩形最多可以向兩邊拓展的寬度，就可以算出以這個矩形高度為高的最大子矩形面積。最後我們求一個最大值即可。

概念

笛卡爾樹的樹根是這一子樹中鍵值最小（或最大）的元素；且對於某個序列的笛卡爾樹，其任一子樹的中序遍歷恰好是對應了原序列中的一段連續區間。

性質

我們會發現笛卡爾樹同時滿足二叉樹搜索和堆的性質：

1. 中序遍歷即為原數組序列
2. 父節點的鍵值均小於（或大於）其左右子節點的鍵值

Efficient construction

A Cartesian tree may be constructed in linear time from its input sequence. One method is to simply process the sequence values in left-to-right order, maintaining the Cartesian tree of the nodes processed so far, in a structure that allows both upwards and downwards traversal of the tree. To process each new value x, start at the node representing the value prior to x in the sequence and follow the path from this node to the root of the tree until finding a value y smaller than x. This node y is the parent of x, and the previous right child of y becomes the new left child of x. The total time for this procedure is linear, because the time spent searching for the parent y of each new node x can be charged against the number of nodes that are removed from the rightmost path in the tree.

An alternative linear-time construction algorithm is based on the all nearest smaller values problem. In the input sequence, one may define the left neighbor of a value x to be the value that occurs prior to x, is smaller than x, and is closer in position to x than any other smaller value. The right neighbor is defined symmetrically. The sequence of left neighbors may be found by an algorithm that maintains a stack containing a subsequence of the input. For each new sequence value x, the stack is popped until it is empty or its top element is smaller than x, and then x is pushed onto the stack. The left neighbor of x is the top element at the time x is pushed. The right neighbors may be found by applying the same stack algorithm to the reverse of the sequence. The parent of x in the Cartesian tree is either the left neighbor of x or the right neighbor of x, whichever exists and has a larger value. The left and right neighbors may also be constructed efficiently by parallel algorithms, so this formulation may be used to develop efficient parallel algorithms for Cartesian tree construction.

Another linear-time algorithm for Cartesian tree construction is based on divide-and-conquer. In particular, the algorithm recursively constructs the tree on each half of the input, and then merging the two trees by taking the right spine of the left tree and left spine of the right tree and performing a standard merging operation. The algorithm is also parallelizable since on each level of recursion, each of the two sub-problems can be computed in parallel, and the merging operation can be efficiently parallelized as well.

HDU1506 Largest Rectangle in a Histogram