題目描述

在 W 星球上有 n 個國家。為了各自國家的經濟發展，他們決定在各個國家 之間建設雙向道路使得國家之間連通。但是每個國家的國王都很吝嗇，他們只願 意修建恰好 n – 1 條雙向道路。 每條道路的修建都要付出一定的費用，這個費用等於道路長度乘以道路兩端 的國家個數之差的絕對值。例如，在下圖中，虛線所示道路兩端分別有 2 個、4 個國家，如果該道路長度為 1，則費用為 1×|2 – 4|=2。圖中圓圈裏的數字表示國 家的編號。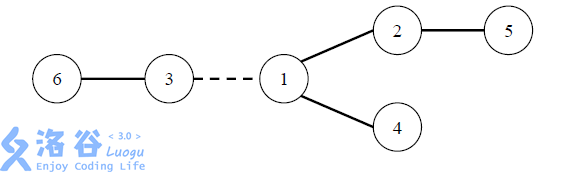

由於國家的數量十分龐大，道路的建造方案有很多種，同時每種方案的修建 費用難以用人工計算，國王們決定找人設計一個軟件，對於給定的建造方案，計 算出所需要的費用。請你幫助國王們設計一個這樣的軟件。

輸入輸出格式

輸入格式：

輸入的第一行包含一個整數 n，表示 W 星球上的國家的數量，國家從 1 到 n 編號。 接下來 n – 1 行描述道路建設情況，其中第 i 行包含三個整數 ai、bi和 ci，表 示第 i 條雙向道路修建在 ai與 bi兩個國家之間，長度為 ci。

輸出格式：

輸出一個整數，表示修建所有道路所需要的總費用。

哇， noi ， 好怕怕，哎？好像有點水．．．

首先這是一棵樹， size[i]表示以i為節點的子樹的大小， 設一個點為i， 它的父親節點為fa， 則顯然兩個點的相差的國家為(n - 2 * size[i]), 這樣可以用bfs或dfs預處理出每個點子樹的大小， 然後枚舉每條邊即可， 洛谷dfs就可以過， 本校oj需要bfs。。。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + 100;
//const int MAXM = 3e3 + 10;

template < typename T > inline void read(T &x) {
    x = 0; T ff = 1, ch = getchar();
    while(!isdigit(ch)) {
        
 
if(ch == ‘-‘) ff = -1;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x *= ff;
}

template < typename T > inline void write(T x) {
    if(x < 0) putchar(‘-‘), x = -x;
    if(x > 9) write(x / 10);
    putchar(x % 10 + ‘0‘);
}

struct edge {
    int y, v, next;
}e[MAXN << 1];
int n, size[MAXN], fa[MAXN];
int tot = 1, lin[MAXN];
int id[MAXN], ti = 0;
ll ans;

inline void add(int xx, int yy, int vv) {
    e[++tot].y = yy;
    e[tot].v = vv;
    e[tot].next = lin[xx];
    lin[xx] = tot;
}


/*void DFS(int x) {
    size[x] = 1;
    for(int i = lin[x], y; i; i = e[i].next) {
        if(size[y = e[i].y]) continue;
        DFS(y);
        ans += (ll)abs(n - 2 * size[y]) * e[i].v;
        size[x] += size[y];
    }
}*/        

void BFS() {
    queue < int > q;
    q.push(1);
    while(!q.empty()) {
        int x = q.front(); q.pop();
        for(int i = lin[x], y; i; i = e[i].next) {
            if((y = e[i].y) != fa[x]) {
                fa[y] = x;
                q.push(y);    
                id[++ti] = y;
            }
        }
    }
}                 

int main() {
//    freopen("1.in", "r", stdin);
    read(n); 
    for(int i = 1; i < n; ++i) {
        int x, y, v;
        read(x); read(y); read(v);
        add(x, y, v);
        add(y, x, v);
    }
    for(int i = 1; i <= n; ++i) 
        size[i] = 1;
    BFS();
    for(int i = ti; i >= 1; --i) 
        size[fa[id[i]]] += size[id[i]];
    for(int i = 2; i <= tot; i += 2) {
        int x = e[i].y, y = e[i ^ 1].y;
        int mi = min(size[x], size[y]);
        ans += (ll)abs(n - 2 * mi) * e[i].v;     
    }
//    DFS(1);
    write(ans);
    return 0;  
}

P1308-道路修建 （noi 2011）