Ceres Solver: 高效的非線性優化庫(二)實戰篇
Ceres Solver: 高效的非線性優化庫(二)實戰篇
接上篇: Ceres Solver: 高效的非線性優化庫(一)
如何求導
Ceres Solver提供了一種自動求導的方案,上一篇我們已經看到。
但有些情況,不能使用自動求導方案。另外兩種方案:解析求導和數值求導。
1. 解析求導
有些情況無法定義模板代價函式。比如殘差函式是庫函式,你無法知道。此時我們可以構建一個NumericDiffCostFunction,例如\[f(x)=10-x\].上面的例子變成
struct NumericDiffCostFunctor { bool operator()(const double* const x, double* residual) const { residual[0] = 10.0 - x[0]; return true; }}; 加入Problem中。 CostFunction* cost_function = new NumericDiffCostFunction<NumericDiffCostFunctor, ceres::CENTRAL, 1, 1>( new NumericDiffCostFunctor); problem.AddResidualBlock(cost_function, NULL, &x);
同自動求導的區別
CostFunction* cost_function =
new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);problem.AddResidualBlock(cost_function, NULL, &x);一般而言,我們推薦自動求導,不適用數值求導。C++模板讓自動求導非常高效,但解析求導速度很慢,且容易造成數值錯誤,收斂較慢。
2. 數值求導
有些情況,自動求導並不能使用。比如,有時候使用最終形勢比自動求導的鏈式法則(chain rule)更方便。
這種情況下,需要提供殘差和雅克比值。為此,我們需要定義一個CostFunction
SizedCostFunction的子類)。下面依舊是\(f(x) = 10 - x\)的例子。
class QuadraticCostFunction : public ceres::SizedCostFunction<1, 1> { public: virtual ~QuadraticCostFunction() {} virtual bool Evaluate(double const* const* parameters, double* residuals, double** jacobians) const { const double x = parameters[0][0]; residuals[0] = 10 - x; // Compute the Jacobian if asked for. if (jacobians != NULL && jacobians[0] != NULL) { jacobians[0][0] = -1; } return true; }};
SimpleCostFunction::Evaluate是輸入引數,residuals是jacobian的輸出。Jacobians是可選項,Evaluate用來檢測它是否非空,否則幫它填充好。此示例下殘差是線性的,雅克比是固定值。
這個方案是比較繁瑣的。除非有必要,推薦使用AutoDiffCostFunction或NumericDiffCostFunction來建立。
3. 更多關於求導的內容
求導是目前Ceres Solver最複雜的內容,有時候使用者需要根據情況旋轉更方便的方案。本節只是大致介紹求導方案。熟悉Numeric和Auto之後,推薦瞭解DynamicAuto,CostFunctionToFunctor,NumericDiffFunctor和ConditionedCostFunction。
實戰之Powell’s Function(一個稍微複雜點的例子)
考慮變數\[x = \left[x_1, x_2, x_3, x_4 \right]\]和
\[
\begin{split}\begin{align}
f_1(x) &= x_1 + 10x_2 \\
f_2(x) &= \sqrt{5} (x_3 - x_4)\\
f_3(x) &= (x_2 - 2x_3)^2\\
f_4(x) &= \sqrt{10} (x_1 - x_4)^2\\
F(x) &= \left[f_1(x),\ f_2(x),\ f_3(x),\ f_4(x) \right]
\end{align}\end{split}
\]
$ F(x) \(是4個引數的函式,有4個殘差,我們希望找到一個最小化\)\frac{1}{2}|F(x)|^2\(的變數\)x\(。第一步,定義一個衡量目標函式的運算元。對於\)f_4(x_1, x_4)$:
struct F4 {
template <typename T>
bool operator()(const T* const x1, const T* const x4, T* residual) const {
residual[0] = T(sqrt(10.0)) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
return true;
}
};類似的我們可以定義F1,F2,F3。利用這些運算元,優化問題可使用下面的方法解決:
double x1 = 3.0; double x2 = -1.0; double x3 = 0.0; double x4 = 1.0;
Problem problem;
// Add residual terms to the problem using the using the autodiff
// wrapper to get the derivatives automatically.
problem.AddResidualBlock(
new AutoDiffCostFunction<F1, 1, 1, 1>(new F1), NULL, &x1, &x2);
problem.AddResidualBlock(
new AutoDiffCostFunction<F2, 1, 1, 1>(new F2), NULL, &x3, &x4);
problem.AddResidualBlock(
new AutoDiffCostFunction<F3, 1, 1, 1>(new F3), NULL, &x2, &x3)
problem.AddResidualBlock(
new AutoDiffCostFunction<F4, 1, 1, 1>(new F4), NULL, &x1, &x4);對於每個ResidualBlock僅僅依賴2個變數。執行examples/powell.cc可以得到相應優化結果。
Initial x1 = 3, x2 = -1, x3 = 0, x4 = 1
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.075000e+02 0.00e+00 1.55e+02 0.00e+00 0.00e+00 1.00e+04 0 4.95e-04 2.30e-03
1 5.036190e+00 1.02e+02 2.00e+01 2.16e+00 9.53e-01 3.00e+04 1 4.39e-05 2.40e-03
2 3.148168e-01 4.72e+00 2.50e+00 6.23e-01 9.37e-01 9.00e+04 1 9.06e-06 2.43e-03
3 1.967760e-02 2.95e-01 3.13e-01 3.08e-01 9.37e-01 2.70e+05 1 8.11e-06 2.45e-03
4 1.229900e-03 1.84e-02 3.91e-02 1.54e-01 9.37e-01 8.10e+05 1 6.91e-06 2.48e-03
5 7.687123e-05 1.15e-03 4.89e-03 7.69e-02 9.37e-01 2.43e+06 1 7.87e-06 2.50e-03
6 4.804625e-06 7.21e-05 6.11e-04 3.85e-02 9.37e-01 7.29e+06 1 5.96e-06 2.52e-03
7 3.003028e-07 4.50e-06 7.64e-05 1.92e-02 9.37e-01 2.19e+07 1 5.96e-06 2.55e-03
8 1.877006e-08 2.82e-07 9.54e-06 9.62e-03 9.37e-01 6.56e+07 1 5.96e-06 2.57e-03
9 1.173223e-09 1.76e-08 1.19e-06 4.81e-03 9.37e-01 1.97e+08 1 7.87e-06 2.60e-03
10 7.333425e-11 1.10e-09 1.49e-07 2.40e-03 9.37e-01 5.90e+08 1 6.20e-06 2.63e-03
11 4.584044e-12 6.88e-11 1.86e-08 1.20e-03 9.37e-01 1.77e+09 1 6.91e-06 2.65e-03
12 2.865573e-13 4.30e-12 2.33e-09 6.02e-04 9.37e-01 5.31e+09 1 5.96e-06 2.67e-03
13 1.791438e-14 2.69e-13 2.91e-10 3.01e-04 9.37e-01 1.59e+10 1 7.15e-06 2.69e-03
Ceres Solver v1.12.0 Solve Report
----------------------------------
Original Reduced
Parameter blocks 4 4
Parameters 4 4
Residual blocks 4 4
Residual 4 4
Minimizer TRUST_REGION
Dense linear algebra library EIGEN
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver DENSE_QR DENSE_QR
Threads 1 1
Linear solver threads 1 1
Cost:
Initial 1.075000e+02
Final 1.791438e-14
Change 1.075000e+02
Minimizer iterations 14
Successful steps 14
Unsuccessful steps 0
Time (in seconds):
Preprocessor 0.002
Residual evaluation 0.000
Jacobian evaluation 0.000
Linear solver 0.000
Minimizer 0.001
Postprocessor 0.000
Total 0.005
Termination: CONVERGENCE (Gradient tolerance reached. Gradient max norm: 3.642190e-11 <= 1.000000e-10)
Final x1 = 0.000292189, x2 = -2.92189e-05, x3 = 4.79511e-05, x4 = 4.79511e-05
實戰之曲線擬合
之前的例子都是不依賴資料的簡單例子。非線性最小二乘法分析最初的目標是把資料擬合稱曲線。現在考慮曲線擬合的資料,公式為\(y = e^{0.3x + 0.1}\)。對其進行取樣並加入方差為\(\sigma = 0.2\)高斯噪聲。我們希望擬合曲線
\[
y = e^{mx + c}
\]
首先我們定義一個模板物件來評估殘差。
struct ExponentialResidual {
ExponentialResidual(double x, double y)
: x_(x), y_(y) {}
template <typename T>
bool operator()(const T* const m, const T* const c, T* residual) const {
residual[0] = T(y_) - exp(m[0] * T(x_) + c[0]);
return true;
}
private:
// Observations for a sample.
const double x_;
const double y_;
};假設我們有觀測資料\(2n\)大小,構建如下問題。
double m = 0.0;
double c = 0.0;
Problem problem;
for (int i = 0; i < kNumObservations; ++i) {
CostFunction* cost_function =
new AutoDiffCostFunction<ExponentialResidual, 1, 1, 1>(
new ExponentialResidual(data[2 * i], data[2 * i + 1]));
problem.AddResidualBlock(cost_function, NULL, &m, &c);
}變異執行examples/curve_fitting.cc得到相應結果。
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.211734e+02 0.00e+00 3.61e+02 0.00e+00 0.00e+00 1.00e+04 0 5.34e-04 2.56e-03
1 1.211734e+02 -2.21e+03 0.00e+00 7.52e-01 -1.87e+01 5.00e+03 1 4.29e-05 3.25e-03
2 1.211734e+02 -2.21e+03 0.00e+00 7.51e-01 -1.86e+01 1.25e+03 1 1.10e-05 3.28e-03
3 1.211734e+02 -2.19e+03 0.00e+00 7.48e-01 -1.85e+01 1.56e+02 1 1.41e-05 3.31e-03
4 1.211734e+02 -2.02e+03 0.00e+00 7.22e-01 -1.70e+01 9.77e+00 1 1.00e-05 3.34e-03
5 1.211734e+02 -7.34e+02 0.00e+00 5.78e-01 -6.32e+00 3.05e-01 1 1.00e-05 3.36e-03
6 3.306595e+01 8.81e+01 4.10e+02 3.18e-01 1.37e+00 9.16e-01 1 2.79e-05 3.41e-03
7 6.426770e+00 2.66e+01 1.81e+02 1.29e-01 1.10e+00 2.75e+00 1 2.10e-05 3.45e-03
8 3.344546e+00 3.08e+00 5.51e+01 3.05e-02 1.03e+00 8.24e+00 1 2.10e-05 3.48e-03
9 1.987485e+00 1.36e+00 2.33e+01 8.87e-02 9.94e-01 2.47e+01 1 2.10e-05 3.52e-03
10 1.211585e+00 7.76e-01 8.22e+00 1.05e-01 9.89e-01 7.42e+01 1 2.10e-05 3.56e-03
11 1.063265e+00 1.48e-01 1.44e+00 6.06e-02 9.97e-01 2.22e+02 1 2.60e-05 3.61e-03
12 1.056795e+00 6.47e-03 1.18e-01 1.47e-02 1.00e+00 6.67e+02 1 2.10e-05 3.64e-03
13 1.056751e+00 4.39e-05 3.79e-03 1.28e-03 1.00e+00 2.00e+03 1 2.10e-05 3.68e-03
Ceres Solver Report: Iterations: 13, Initial cost: 1.211734e+02, Final cost: 1.056751e+00, Termination: CONVERGENCE
Initial m: 0 c: 0
Final m: 0.291861 c: 0.131439使用初值\(m=0, c=0\), 初始目標函式值為\(121.173\)。Ceres計算得到\(m=0.291, c=0.131\).目標函式值為\(1.056\)。但這同原始模型不一樣,但也是合理的。通過帶噪聲的資料恢復模型會得到一定的偏差。實際上,即使使用原始模型資料,偏差更大。
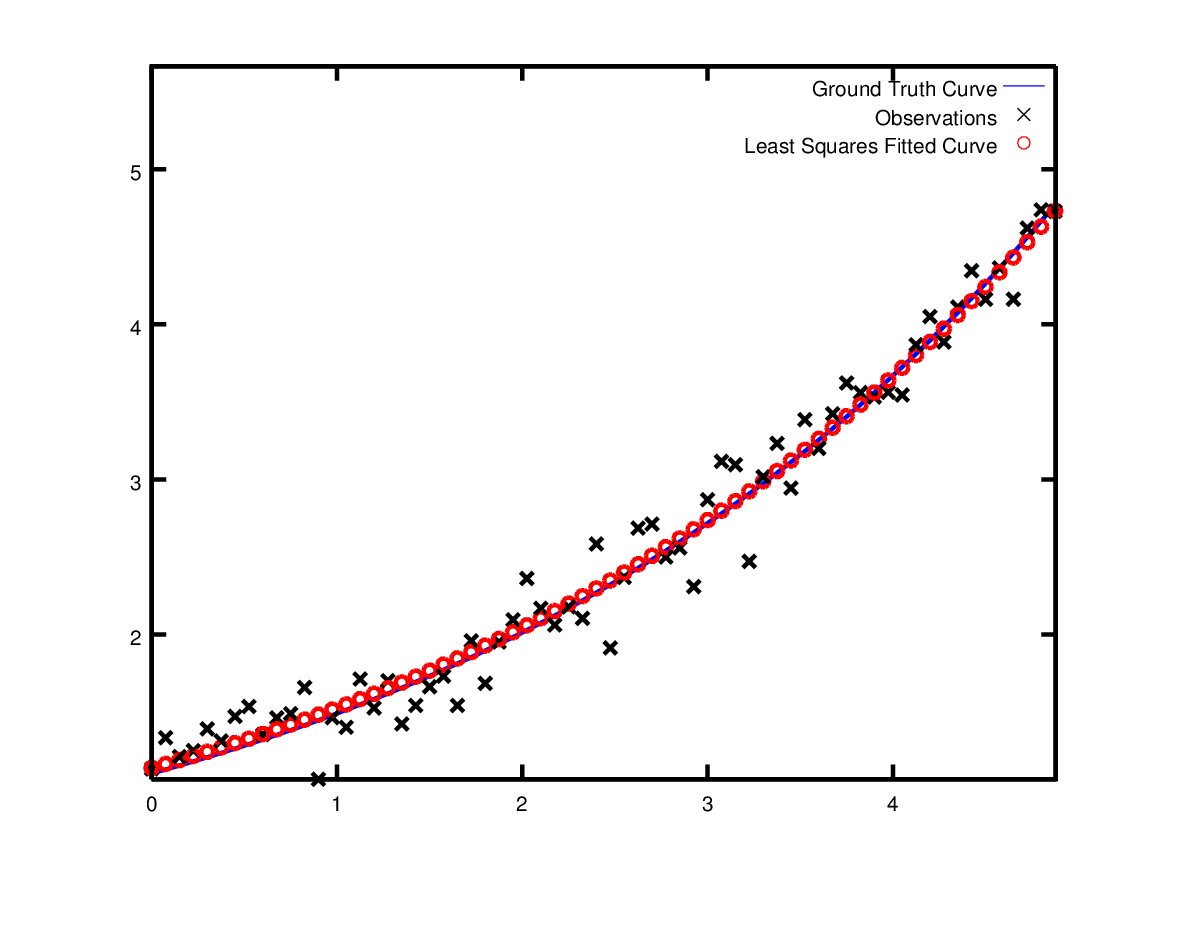
實戰之曲線魯棒擬合
現在假設資料有一些我們並不在模型的值。如果使用這些做擬合,模型會離真實值有所偏差。如下圖。
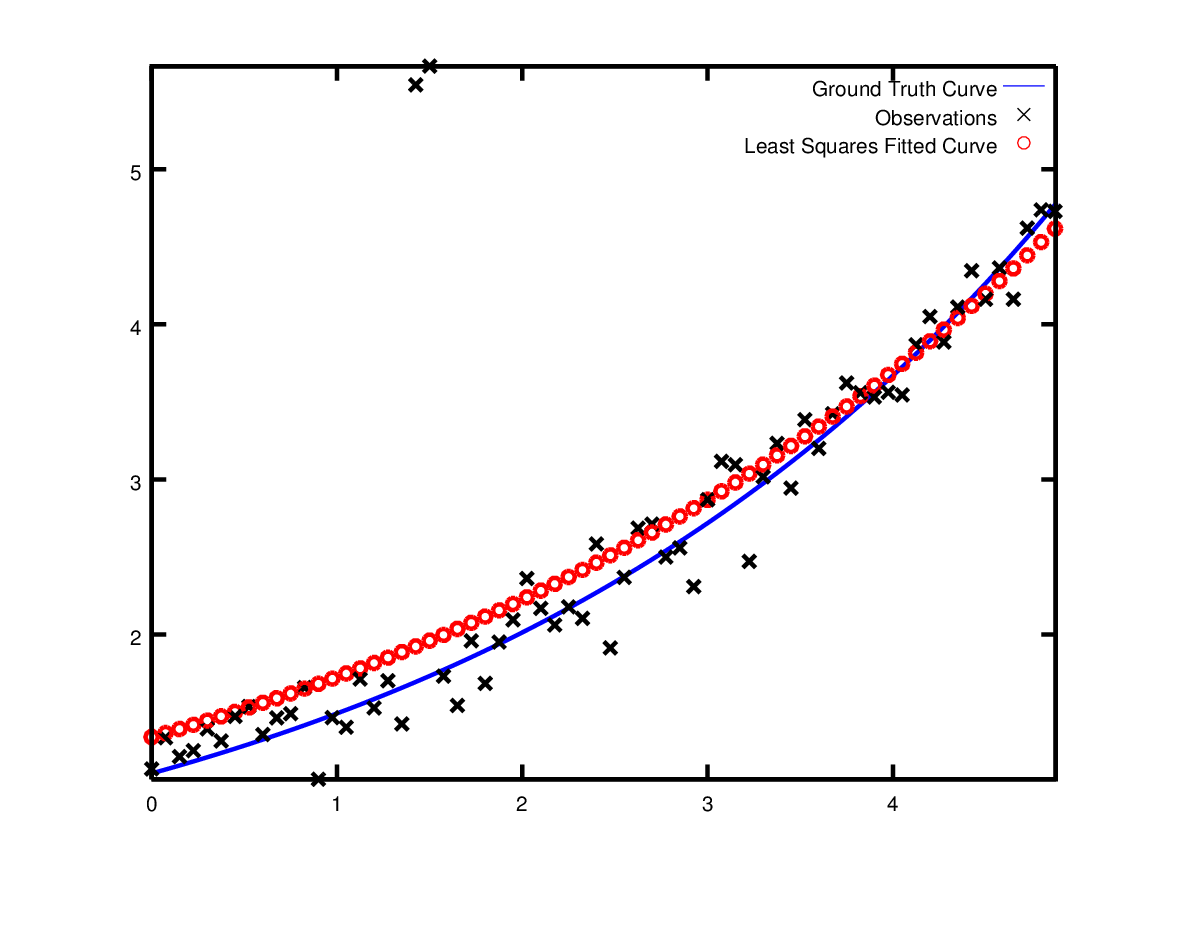
為了處理這些噪點,一個技巧是使用LossFunction。此函式減小大偏差對整個殘差模組的影響。大偏差經常屬於Outliers。加入殘差函式,我們修要做修改
problem.AddResidualBlock(cost_function, NULL , &m, &c);改為
problem.AddResidualBlock(cost_function, new CauchyLoss(0.5) , &m, &c);CauchyLoss是Ceres Solver發明的損失函式之一。0.5是損失函式的尺度。加入損失函式後,我們獲得更好的擬合結果。

下一篇文章裡,我們重點介紹Ceres是計算機三維視覺裡的重要應用:光束平差法(Bundle Adjustment),一般簡稱BA
