Ceres Solver: 高效的非線性優化庫（一）

注：本文基於Ceres官方文件，大部分由英文翻譯而來。可作為非官方參考文件。

簡介

Ceres，原意是穀神星，是發現不久的一顆軌道在木星和火星之間“矮行星”（冥王星降級之後，同為矮行星）。Google開源了Ceres Solver庫，是一個解很多非線性最優化問題的高效、方便的工具。

• 官方網站：http://ceres-solver.org/
• 原始碼地址：https://github.com/ceres-solver/ceres-solver
• 主要特性：速度快、介面豐富方便、執行穩定。

安裝

引用地址：http://ceres-solver.org/installation.html

目前開源方未提供可安裝檔案。需要原始碼下載編譯。
下載方式，首先安裝Git。Git，主流版本管理工具，使用方法見官方文件。
git clone https://ceres-solver.googlesource.com/ceres-solver
依賴項：

• Eigen，好用的數學庫，無原始碼，全部是標頭檔案。
• CMake，工程生產工具，跨平臺。
• Glog，log庫，選裝。TBB，選裝。
• Gflags，SuiteSparse， CXSparse，BLAS，LAPACK主要是用來解大型稀疏矩陣的，必須要裝。

Linux系統下可以很方便的用命令列安裝各種庫。
sudo apt-get install cmake libatalas-base-dev libeigen3-dev libsuitesparse-dev

mkdir build & cmake ..
make -j4
sudo make install

可以愉快的使用Ceres啦！先看Example，有示例嘛，學起來更快！
直接執行一下如下結果，
bin/simple_bundle_adjuster ../ceres-solver-1.14.0/data/problem-16-22106-pre.txt
似乎成功了？輸出很多內容，好像看不懂。沒關係，能執行成功，說明Ceres安裝成功，可以愉快的使用。
注：這裡解釋的是更多在linux下面安裝。Widows下基本大同小異，需要花點時間的是SuiteSparse幾個三方庫的安裝和配置，不過也並不複雜。

實戰

找到並使用Ceres-Solver

推薦使用CMake工具找到並使用Ceres，類似OpenCV。

什麼是非線性最小二乘問題

Ceres-Solver可解形如下列公式的問題
\[ \begin{split}\min_{\mathbf{x}} &\quad \frac{1}{2}\sum_{i} \rho_i\left(\left\|f_i\left(x_{i_1}, ... ,x_{i_k}\right)\right\|^2\right) \\ \text{s.t.} &\quad l_j \le x_j \le u_j\end{split} \]
有點複雜，具體什麼含義呢？
比如，平面（空間）很多帶噪聲的點，我們要擬合一條直線（平面）或曲線。比如，三維視覺的全域性最優問題。

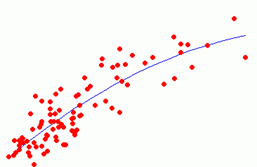
注意：直線擬合一般也可用線性迴歸解決。
公式中的目標函式集合稱之為殘差項，目標是是這個值最小；\(f_i\)函式被稱為代價函式，由引數\(x_i\)組成。\(l_i, u_j\)則是函式的取值範圍。
下面用了一個具體的示例說明。
求如下目標函式的最小值。
\[ \frac{1}{2}(10 -x)^2. \]
通過求二階導數我們很容易知道x=10時，最小值取0.但這裡我們嘗試用Ceres來解決。

• 第一步，代價函式\(f(x) = 10 - x\).

struct CostFunctor {
   template <typename T>
   bool operator()(const T* const x, T* residual) const {
     residual[0] = T(10.0) - x[0];
     return true;
   }};

程式碼中符號（）是一個模板方法，輸入是同一型別。

• 第二步，構建非線性最小二乘問題。

int main(int argc, char** argv)
 {
  // The variable to solve for with its initial value.
  double initial_x = 5.0;
  double x = initial_x;

  // Build the problem.
  Problem problem;

  // Set up the only cost function (also known as residual). This uses
  // auto-differentiation to obtain the derivative (jacobian).
  CostFunction* cost_function =
      new AutoDiffCostFunction<CostFunctor, 1, 1>(new CostFunctor);
  problem.AddResidualBlock(cost_function, NULL, &x);

  // Run the solver!
  Solver::Options options;
  options.linear_solver_type = ceres::DENSE_QR;
  options.minimizer_progress_to_stdout = true;
  Solver::Summary summary;
  Solve(options, &problem, &summary);

  std::cout << summary.BriefReport() << "\n";
  std::cout << "x : " << initial_x
            << " -> " << x << "\n";
  return 0;
}

AutoDiffCostFunction用CostFunctor作為輸入，並提供了一個自動求微分的介面。
計算example/helloworld.cc會得到相應輸出結果。

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  4.512500e+01    0.00e+00    9.50e+00   0.00e+00   0.00e+00  1.00e+04       0    5.33e-04    3.46e-03
   1  4.511598e-07    4.51e+01    9.50e-04   9.50e+00   1.00e+00  3.00e+04       1    5.00e-04    4.05e-03
   2  5.012552e-16    4.51e-07    3.17e-08   9.50e-04   1.00e+00  9.00e+04       1    1.60e-05    4.09e-03
Ceres Solver Report: Iterations: 2, Initial cost: 4.512500e+01, Final cost: 5.012552e-16, Termination: CONVERGENCE
x : 0.5 -> 10

實際上此示例是個線性問題，卻能很好的解釋非線性優化的思想。
接下來的文章會處理一些更加複雜的問題，敬請期待