資料結構與演算法(一):帶你瞭解時間複雜度和空間複雜度到底是什麼?


1. 前言
演算法(Algorithm)是指用來操作資料、解決程式問題的一組方法。對於同一個問題,使用不同的演算法,也許最終得到的結果是一樣的,但在過程中消耗的資源和時間卻會有很大的區別。那麼我們應該如何去衡量不同演算法之間的優劣呢?
主要還是從演算法所佔用的「時間」和「空間」兩個維度去考量。
時間維度:是指執行當前演算法所消耗的時間,我們通常用「時間複雜度」來描述。
空間維度:是指執行當前演算法需要佔用多少記憶體空間,我們通常用「空間複雜度」來描述。
因此,評價一個演算法的效率主要是看它的時間複雜度和空間複雜度情況。然而,有的時候時間和空間卻又是「魚和熊掌」,不可兼得的,那麼我們就需要從中去取一個平衡點。
2. 演算法的介紹
排序也稱排序演算法(Sort Algorithm),排序是將一組資料,依指定的順序進行排列的過程。
3. 排序的分類
3.1 內部排序
指將需要處理的所有資料都載入到內部儲存器(記憶體)中進行排序。
3.2 外部排序法
資料量過大,無法全部載入到記憶體中,需要藉助外部儲存(檔案等)進行排序。
3.3 常見的排序演算法分類(見下圖)

4. 演算法的時間複雜度
4.1 度量程式(演算法)執行時間方法
4.1.1 事後統計的方法
這種方法可行, 但是有兩個問題:一是要想對設計的演算法的執行效能進行評測,需要實際執行該程式;二是所得時間的統計量依賴於計算機的硬體、軟體等環境因素, 這種方式,要在同一臺計算機的相同狀態下執行,才能比較哪個演算法速度更快。
4.1.2 事前估算的方法
因事後統計方法更多的依賴於計算機的硬體、軟體等環境因素,有時容易掩蓋演算法本身的優劣。因此人們常常採用事前分析估算的方法。
在編寫程式前,依據統計方法對演算法進行估算。一個用高階語言編寫的程式在計算機上執行時所消耗的時間取決於下列因素:
(1) 演算法採用的策略、方法
(2) 編譯產生的程式碼質量
(3) 問題的輸入規模
(4) 機器執行指令的速度。
通過分析某個演算法的時間複雜度來判斷哪個演算法更優。
4.2 時間頻度
4.2.1 基本介紹
時間頻度:一個演算法花費的時間與演算法中語句的執行次數成正比例,哪個演算法中語句執行次數多,它花費時間就多。 一個演算法中的語句執行次數稱為語句頻度或時間頻度。記為 T(n)。
舉例說明-基本案例
比如計算 1-1000 所有數字之和, 我們設計兩種演算法:
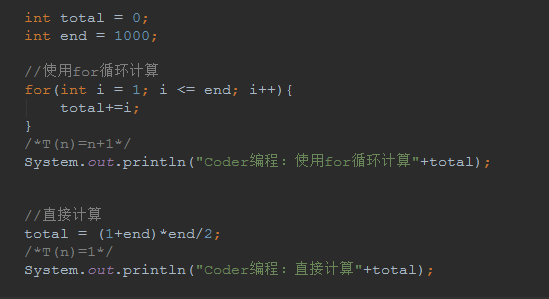
舉例說明-忽略常數項
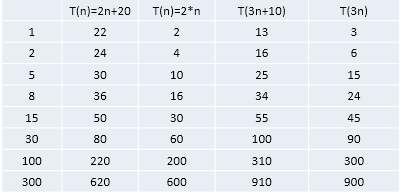
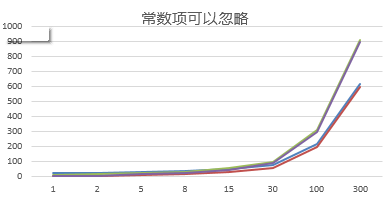
結論:
1) 2n+20 和 2n 隨著 n 變大,執行曲線無限接近, 20 可以忽略
2) 3n+10 和 3n 隨著 n 變大,執行曲線無限接近, 10 可以忽略
舉例說明-忽略低次項
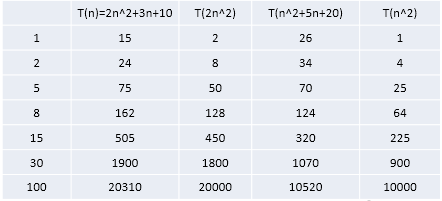
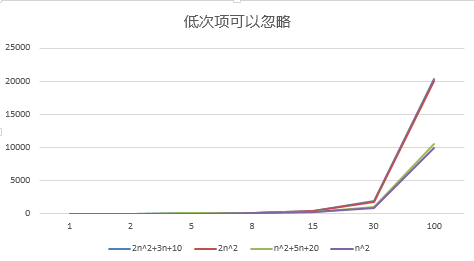
結論:
1) 2n^2+3n+10 和 2n^2 隨著 n 變大, 執行曲線無限接近, 可以忽略 3n+10
2) n^2+5n+20 和 n^2 隨著 n 變大,執行曲線無限接近, 可以忽略 5n+20
舉例說明-忽略係數
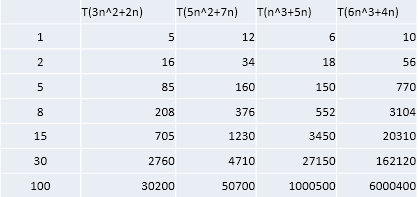
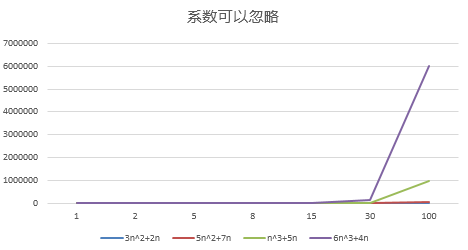
結論:
1) 隨著 n 值變大,5n^2+7n 和 3n^2 + 2n ,執行曲線重合, 說明 這種情況下, 5 和 3 可以忽略。
2) 而 n^3+5n 和 6n^3+4n ,執行曲線分離,說明多少次方式關鍵
4.3 時間複雜度
1) 一般情況下,演算法中的基本操作語句的重複執行次數是問題規模 n 的某個函式,用 T(n)表示,若有某個輔助函式 f(n),使得當 n 趨近於無窮大時,T(n) / f(n) 的極限值為不等於零的常數,則稱 f(n)是 T(n)的同數量級函式。記作 T(n)= O( f(n) ),稱O( f(n) ) 為演算法的漸進時間複雜度,簡稱時間複雜度。
2) T(n) 不同,但時間複雜度可能相同。 如:T(n)=n²+7n+6 與 T(n)=3n²+2n+2 它們的 T(n) 不同,但時間複雜度相同,都為 O(n²)。
3) 計算時間複雜度的方法:
- 用常數 1 代替執行時間中的所有加法常數 T(n)=n²+7n+6 => T(n)=n²+7n+1
- 修改後的執行次數函式中,只保留最高階項 T(n)=n²+7n+1 => T(n) = n²
- 去除最高階項的係數 T(n) = n² => T(n) = n² => O(n²)
4.4 常見的時間複雜度
1) 常數階 O(1)
2) 對數階 O(log2n)
3) 線性階 O(n)
4) 線性對數階 O(nlog2n)
5) 平方階 O(n^2)
6) 立方階 O(n^3)
7) k 次方階 O(n^k)
8) 指數階 O(2^n)
4.4.1 常見的時間複雜度對應的圖
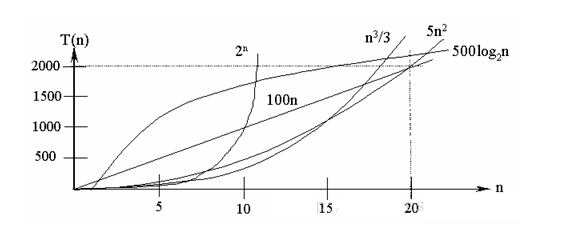
說明:
1) 常見的演算法時間複雜度由小到大依次為:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<Ο(nk)<Ο(2n) ,隨著問題規模 n 的不斷增大,上述時間複雜度不斷增大,演算法的執行效率越低
2) 從圖中可見,我們應該儘可能避免使用指數階的演算法
4.4.1.1 常數階 O(1)
無論程式碼執行了多少行,只要是沒有迴圈等複雜結構,那這個程式碼的時間複雜度就都是O(1)。

上述程式碼在執行的時候,它消耗的時候並不隨著某個變數的增長而增長,那麼無論這類程式碼有多長,即使有幾萬幾十萬行,都可以用O(1)來表示它的時間複雜度。
4.4.1.2 對數階 O(log2n)
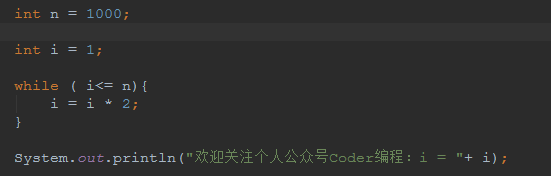
說明: 在while迴圈裡面,每次都將 i 乘以 2,乘完之後,i 距離 n 就越來越近了。假設迴圈x次之後,i 就大於 n 了,此時這個迴圈就退出了,也就是說 2 的 x 次方等於 n,那麼 x = log2n也就是說當迴圈 log2n 次以後,這個程式碼就結束了。因此這個程式碼的時間複雜度為:O(log2n) 。 O(log2n) 的這個2 時間上是根據程式碼變化的,i = i * 3 ,則是 O(log3n) 。

4.4.1.3 線性階 O(n)

說明: 這段程式碼,for迴圈裡面的程式碼會執行n遍,因此它消耗的時間是隨著n的變化而變化的,因此這類程式碼都可以用O(n)來表示它的時間複雜度。
4.4.1.4 線性對數階 O(nlogN)

說明: 線性對數階O(nlogN) 其實非常容易理解,將時間複雜度為O(logn)的程式碼迴圈N遍的話,那麼它的時間複雜度就是 n * O(logN),也就是了O(nlogN)。
4.4.1.5 平方階 O(n²)

說明: 平方階O(n²) 就更容易理解了,如果把 O(n) 的程式碼再巢狀迴圈一遍,它的時間複雜度就是 O(n²),這段程式碼其實就是嵌套了2層n迴圈,它的時間複雜度就是 O(nn),即 O(n²) 如果將其中一層迴圈的n改成m,那它的時間複雜度就變成了 O(mn)
4.4.1.6 立方階 O(n³)、K 次方階 O(n^k)
說明: 參考上面的 O(n²) 去理解就好了,O(n³)相當於三層 n 迴圈,其它的類似
4.5 平均時間複雜度和最壞時間複雜度
1) 平均時間複雜度是指所有可能的輸入例項均以等概率出現的情況下,該演算法的執行時間。
2) 最壞情況下的時間複雜度稱最壞時間複雜度。 一般討論的時間複雜度均是最壞情況下的時間複雜度。這樣做的原因是:最壞情況下的時間複雜度是演算法在任何輸入例項上執行時間的界限,這就保證了演算法的執行時間不會比最壞情況更長。
3) 平均時間複雜度和最壞時間複雜度是否一致,和演算法有關(如下圖)。
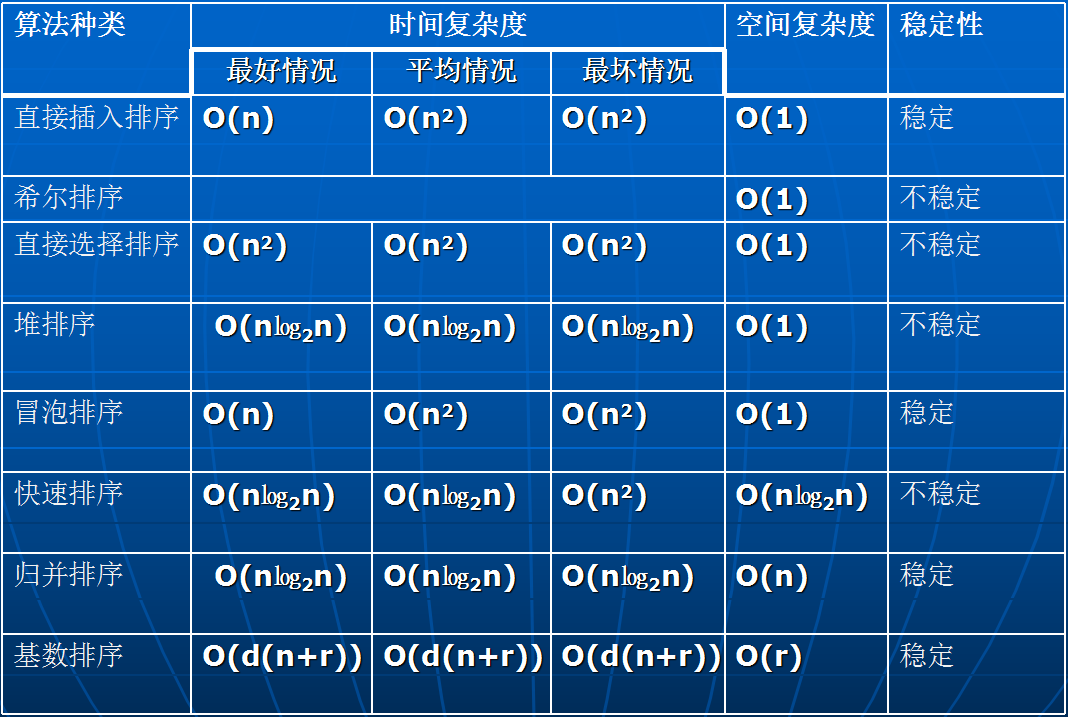
4. 空間複雜度
4.1 簡介
1) 類似於時間複雜度的討論,一個演算法的空間複雜度(Space Complexity)定義為該演算法所耗費的儲存空間,它也是問題規模 n 的函式。
2) 空間複雜度(Space Complexity)是對一個演算法在執行過程中臨時佔用儲存空間大小的量度。有的演算法需要佔用的臨時工作單元數與解決問題的規模 n 有關,它隨著 n 的增大而增大,當 n 較大時,將佔用較多的儲存單元,例如快速排序和歸併排序演算法, 基數排序就屬於這種情況
3) 在做演算法分析時,主要討論的是時間複雜度。 從使用者使用體驗上看,更看重的程式執行的速度。一些快取產品(redis, memcache)和演算法(基數排序)本質就是用空間換時間。
4.2 定義
演算法的空間複雜度通過計算演算法所需的儲存空間實現,演算法的空間複雜度的計算公式記作:S(n)=O(f(n)),其中,n為問題的規模,f(n)為語句關於n所佔儲存空間的函式。
4.3 舉例說明
例如:如何判斷某年是不是閏年?
方法一
寫一個演算法,每給一個年份,就可以通過該演算法計算得到是否閏年的結果。
方法二
先建立一個所有年份的陣列,然後把所有的年份按下標的數字對應,如果是閏年,則此陣列元素的值是1,如果不是元素的值則為0。這樣,所謂的判斷某一年是否為閏年就變成了查詢這個陣列某一個元素的值的問題。
第一種方法相比起第二種來說很明顯非常節省空間,但每一次查詢都需要經過一系列的計算才能知道是否為閏年。
第二種方法雖然需要在記憶體裡儲存所有年份的陣列,但是每次查詢只需要一次索引判斷即可。
這是空間和時間互換的例子。到底哪一種方法好?其實還是要看具體用在什麼地方。
文末
歡迎關注個人微信公眾號:Coder程式設計
獲取最新原創技術文章和免費學習資料,更有大量精品思維導圖、面試資料、PMP備考資料等你來領,方便你隨時隨地學習技術知識!
新建了一個qq群:315211365,歡迎大家進群交流一起學習。謝謝了!也可以介紹給身邊有需要的朋友。
文章收錄至
Github: https://github.com/CoderMerlin/coder-programming
Gitee: https://gitee.com/573059382/coder-programming
歡迎關注並star~

