資料結構與演算法（七）：迷宮回溯和八皇后問題
阿新 • • 發佈：2020-06-27
## 一、迷宮回溯問題
### 1.問題
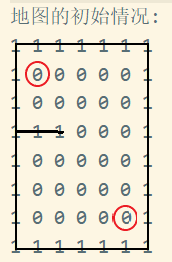
一個7*8的陣列模擬迷宮，障礙用1表示，通路使用0表示，給定起點（1,1）和終點（6,5），要求給出起點到終點的通路
### 2.解題思路
1. 首先，我們需要給程式一個尋向的基本策略，我們先假定尋向順序為“下-右-上-左”，也就是說從起點出發，先往下走，往下走不通就往右.....以此類推
2. 然後我們需要給走過的路一個標記，暫記為2
3. 而當從一個方向走到一個只能原路返回的死衚衕時，就給這段路標記為3
4. 當抵達終點座標（6,5）時程式結束
### 3.程式碼實現
#### 3.1生成地圖
~~~java
/**
* 建立一個二維陣列,用於模擬8*7迷宮
* 使用1表示不可通過的實心方塊，0表示可通過磚塊
* （6,5）為預設終點，（1,1）為預設起點
* @return
*/
public static int[][] getMap(){
int[][] map = new int[8][7];
//上下全置為1
for(int i = 0;i <7 ;i++){
map[0][i] = 1;
map[7][i] = 1;
}
//左右全置為1
for(int i = 0;i < 8;i++){
map[i][0] = 1;
map[i][6] = 1;
}
//設定擋板
map[3][1] = 1;
map[3][2] = 1;
//輸出地圖
System.out.println("地圖的初始情況:");
showMap(map);
return map;
}
/**
* 展示地圖
* @param map
*/
public static void showMap(int[][] map) {
for(int i = 0;i < 8;i++){
for(int j = 0;j < 7;j++){
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
~~~
#### 3.2 尋路邏輯的實現
對於這個尋路程式，我們可以看見，往四個方向走的過程實際上除了方向外動作上是一樣的；而具體分析同一個方向，每走過一個座標的動作也是一樣的，我們對流程進行分析：
1. 出發，先往下走，判斷下一格有沒有障礙（`int[x][y]==1`）
2. 如果沒有障礙，就繼續往下走，然後重複步驟1到碰到障礙為止
3. 如果有障礙，就按“下-右-上-左”的順序，換個方向，然後重複步驟1到碰到障礙為止
4. 如果找到了（6,5）就結束
表現為程式碼實際上就是一個遞迴的過程：
- 找路是方法體
- 找到了（6,5）或者死衚衕是終止條件
~~~java
/**
* 給定起始點，根據地圖找路
* 使用2表示可以走通的路，使用3表示走過但是不通的路
* @param map 地圖二維陣列
* @param x 起始點橫座標
* @param y 起始點縱座標
* @return
*/
public static boolean findWay(int[][] map, int x, int y) {
//如果走到了終點就終止
if (map[6][5] == 2){
return true;
}else {
//只有為0的路才能通過
if (map[y][x] == 0) {
//如果該點可以走通就打上標記
map[y][x] = 2;
if (findWay(map, x, y + 1)) {
//向下遞迴
return true;
} else if (findWay(map, x + 1, y)) {
//向右遞迴
return true;
} else if (findWay(map, x, y - 1)) {
//向上遞迴
return true;
} else if (findWay(map, x - 1, y)) {
//向左遞迴
return true;
} else {
//都走不通說明是死衚衕
map[y][x] = 3;
return false;
}
}else {
//不為0說明要麼是死路要麼是障礙
return false;
}
}
}
~~~
#### 3.3 執行結果
將`findWay()`方法中的終止條件從`map[6][5] == 2`換成其他座標即可更換終點位置，
棋盤大小和障礙物位置不影響`findWay()`方法尋路。
## 二、八皇后問題
### 1.問題
皇后問題，一個古老而著名的問題，是**回溯演算法**的典型案例。該問題由國際西洋棋棋手馬克斯·貝瑟爾於 1848 年提出：
在 8×8 格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一斜線上，求有多少種擺法？
### 2.解題思路
1. 首先，我們先使用一個長度為8陣列來表示八皇后的擺放位置，**陣列下標+1即表示棋盤的第幾行**，**陣列下標對應的存放的數字+1即為棋盤的第幾列**。舉個例子：
arr = {0,2,3,8,4,6,2,7}
其中，元素0下標為0，即表示**第一行第一列**；元素2下標為1，即表示**第二行第三列**......以此類推。
2. 任意假設任意座標分標為`(x1,y1)，(x2,y2)`，也就是用陣列表示為`arr[x1]=y1，arr[x2]=y2`的兩個皇后不允許在同一列，我們可以理解為：
`arr[x1] != arr[x2]`;
而任意座標的皇后不允許在同一斜線，即`(x2-x1)=(y2-y1)`，也就是斜率不應當相同，我們可以理解為：
`Math.abs(x2-x1) != Math.abs(arr[x2]-arr[x1])`
（注：`Math.abs()`為求絕對值方法）
### 3.程式碼實現
#### 3.1 檢查擺放位置的程式碼實現
在前面明確瞭如何用陣列表示位置，以及如何檢查皇后是否允許擺放後，我們有如下程式碼：
~~~java
//表示皇后位置的陣列
int[] arr = new int[8];
/**
* 檢查第n個皇后是否與前面擺放的皇后衝突
* @param n
* @return
*/
public boolean check(int n) {
//檢查第n層之前的皇后位置
for (int i = 0; i < n; i++) {
// arr[i] == arr[n] 檢查是否同一列
// Math.abs(n - i) == Math.abs(arr[n] - arr[i]) 檢查是否同一斜線
if (arr[i] == arr[n] ||
Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
return false;
}
}
return true;
}
~~~
#### 3.2 完整程式碼
接著我們需要考慮如何使用遞迴方法來做到以下效果：
使用一個方法遍歷第n行的每一列，檢查每一列是否可以放置皇后：
1. 如果可以放置皇后，將位置出入arr[n]中，然後遞迴呼叫自己，傳入n+1開始遍歷下一行.....以此類推
2. 如果不可以放置皇后，就跳過該列檢查下一列，如果可以就重複步驟1
3. 若n行中全部位置都不合適，則結束本層返回上一層n-1層，重複步驟1
4. 如果最後n=8，即八個皇后全部放置完畢，記一次完成擺放，然後結束遞迴返回第一層，繼續檢查第一層的下一列
最終程式碼實現結果如下：
~~~java
/**
* @Author：黃成興
* @Date：2020-06-26 20:53
* @Description：八皇后問題
*/
public class EightQueens {
public static void main(String[] args) {
EightQueens eightQueens = new EightQueens();
eightQueens.set(0);
System.out.println("共有擺法：" + eightQueens.count);
}
//記錄八皇后有幾種擺法
int count = 0;
//表示皇后位置的陣列
int[] arr = new int[8];
/**
* 擺放皇后
* @param n 第幾個皇后
*/
private void set(int n) {
//如果放置好了第8個皇后
if (n == 8){
show();
//記錄一種擺放方式
count++;
//回到第一層繼續遞迴
return;
}
//遍歷第n行的每一列
for (int i = 0; i < 8; i++) {
//將該皇后放置在第n行第i列
arr[n] = i;
//檢查放置位置是否合適
if (check(n)){
//如果位置合適，就遞迴找下一個（n+1）皇后的擺放位置
set(n + 1);
}
//如果位置不合適，就跳過這一列檢查下一列
}
}
/**
* 檢查第n個皇后是否與前面擺放的皇后衝突
* @param n
* @return
*/
public boolean check(int n) {
//檢查第n層之前的皇后位置
for (int i = 0; i < n; i++) {
// arr[i] == arr[n] 檢查是否同一列
// Math.abs(n - i) == Math.abs(arr[n] - arr[i]) 檢查是否同一斜線
if (arr[i] == arr[n] ||
Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
return false;
}
}
return true;
}
/**
* 展示某一擺法中八皇后的擺放位置
*/
public void show() {
for (int i : arr) {
System.out.print(i + " ");
}
System.out.println();
}
}
~~~
### 2.解題思路
1. 首先，我們需要給程式一個尋向的基本策略，我們先假定尋向順序為“下-右-上-左”，也就是說從起點出發，先往下走，往下走不通就往右.....以此類推
2. 然後我們需要給走過的路一個標記，暫記為2
3. 而當從一個方向走到一個只能原路返回的死衚衕時，就給這段路標記為3
4. 當抵達終點座標（6,5）時程式結束
### 3.程式碼實現
#### 3.1生成地圖
~~~java
/**
* 建立一個二維陣列,用於模擬8*7迷宮
* 使用1表示不可通過的實心方塊，0表示可通過磚塊
* （6,5）為預設終點，（1,1）為預設起點
* @return
*/
public static int[][] getMap(){
int[][] map = new int[8][7];
//上下全置為1
for(int i = 0;i <7 ;i++){
map[0][i] = 1;
map[7][i] = 1;
}
//左右全置為1
for(int i = 0;i < 8;i++){
map[i][0] = 1;
map[i][6] = 1;
}
//設定擋板
map[3][1] = 1;
map[3][2] = 1;
//輸出地圖
System.out.println("地圖的初始情況:");
showMap(map);
return map;
}
/**
* 展示地圖
* @param map
*/
public static void showMap(int[][] map) {
for(int i = 0;i < 8;i++){
for(int j = 0;j < 7;j++){
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
~~~
#### 3.2 尋路邏輯的實現
對於這個尋路程式，我們可以看見，往四個方向走的過程實際上除了方向外動作上是一樣的；而具體分析同一個方向，每走過一個座標的動作也是一樣的，我們對流程進行分析：
1. 出發，先往下走，判斷下一格有沒有障礙（`int[x][y]==1`）
2. 如果沒有障礙，就繼續往下走，然後重複步驟1到碰到障礙為止
3. 如果有障礙，就按“下-右-上-左”的順序，換個方向，然後重複步驟1到碰到障礙為止
4. 如果找到了（6,5）就結束
表現為程式碼實際上就是一個遞迴的過程：
- 找路是方法體
- 找到了（6,5）或者死衚衕是終止條件
~~~java
/**
* 給定起始點，根據地圖找路
* 使用2表示可以走通的路，使用3表示走過但是不通的路
* @param map 地圖二維陣列
* @param x 起始點橫座標
* @param y 起始點縱座標
* @return
*/
public static boolean findWay(int[][] map, int x, int y) {
//如果走到了終點就終止
if (map[6][5] == 2){
return true;
}else {
//只有為0的路才能通過
if (map[y][x] == 0) {
//如果該點可以走通就打上標記
map[y][x] = 2;
if (findWay(map, x, y + 1)) {
//向下遞迴
return true;
} else if (findWay(map, x + 1, y)) {
//向右遞迴
return true;
} else if (findWay(map, x, y - 1)) {
//向上遞迴
return true;
} else if (findWay(map, x - 1, y)) {
//向左遞迴
return true;
} else {
//都走不通說明是死衚衕
map[y][x] = 3;
return false;
}
}else {
//不為0說明要麼是死路要麼是障礙
return false;
}
}
}
~~~
#### 3.3 執行結果
將`findWay()`方法中的終止條件從`map[6][5] == 2`換成其他座標即可更換終點位置，
棋盤大小和障礙物位置不影響`findWay()`方法尋路。
## 二、八皇后問題
### 1.問題
皇后問題，一個古老而著名的問題，是**回溯演算法**的典型案例。該問題由國際西洋棋棋手馬克斯·貝瑟爾於 1848 年提出：
在 8×8 格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一斜線上，求有多少種擺法？
### 2.解題思路
1. 首先，我們先使用一個長度為8陣列來表示八皇后的擺放位置，**陣列下標+1即表示棋盤的第幾行**，**陣列下標對應的存放的數字+1即為棋盤的第幾列**。舉個例子：
arr = {0,2,3,8,4,6,2,7}
其中，元素0下標為0，即表示**第一行第一列**；元素2下標為1，即表示**第二行第三列**......以此類推。
2. 任意假設任意座標分標為`(x1,y1)，(x2,y2)`，也就是用陣列表示為`arr[x1]=y1，arr[x2]=y2`的兩個皇后不允許在同一列，我們可以理解為：
`arr[x1] != arr[x2]`;
而任意座標的皇后不允許在同一斜線，即`(x2-x1)=(y2-y1)`，也就是斜率不應當相同，我們可以理解為：
`Math.abs(x2-x1) != Math.abs(arr[x2]-arr[x1])`
（注：`Math.abs()`為求絕對值方法）
### 3.程式碼實現
#### 3.1 檢查擺放位置的程式碼實現
在前面明確瞭如何用陣列表示位置，以及如何檢查皇后是否允許擺放後，我們有如下程式碼：
~~~java
//表示皇后位置的陣列
int[] arr = new int[8];
/**
* 檢查第n個皇后是否與前面擺放的皇后衝突
* @param n
* @return
*/
public boolean check(int n) {
//檢查第n層之前的皇后位置
for (int i = 0; i < n; i++) {
// arr[i] == arr[n] 檢查是否同一列
// Math.abs(n - i) == Math.abs(arr[n] - arr[i]) 檢查是否同一斜線
if (arr[i] == arr[n] ||
Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
return false;
}
}
return true;
}
~~~
#### 3.2 完整程式碼
接著我們需要考慮如何使用遞迴方法來做到以下效果：
使用一個方法遍歷第n行的每一列，檢查每一列是否可以放置皇后：
1. 如果可以放置皇后，將位置出入arr[n]中，然後遞迴呼叫自己，傳入n+1開始遍歷下一行.....以此類推
2. 如果不可以放置皇后，就跳過該列檢查下一列，如果可以就重複步驟1
3. 若n行中全部位置都不合適，則結束本層返回上一層n-1層，重複步驟1
4. 如果最後n=8，即八個皇后全部放置完畢，記一次完成擺放，然後結束遞迴返回第一層，繼續檢查第一層的下一列
最終程式碼實現結果如下：
~~~java
/**
* @Author：黃成興
* @Date：2020-06-26 20:53
* @Description：八皇后問題
*/
public class EightQueens {
public static void main(String[] args) {
EightQueens eightQueens = new EightQueens();
eightQueens.set(0);
System.out.println("共有擺法：" + eightQueens.count);
}
//記錄八皇后有幾種擺法
int count = 0;
//表示皇后位置的陣列
int[] arr = new int[8];
/**
* 擺放皇后
* @param n 第幾個皇后
*/
private void set(int n) {
//如果放置好了第8個皇后
if (n == 8){
show();
//記錄一種擺放方式
count++;
//回到第一層繼續遞迴
return;
}
//遍歷第n行的每一列
for (int i = 0; i < 8; i++) {
//將該皇后放置在第n行第i列
arr[n] = i;
//檢查放置位置是否合適
if (check(n)){
//如果位置合適，就遞迴找下一個（n+1）皇后的擺放位置
set(n + 1);
}
//如果位置不合適，就跳過這一列檢查下一列
}
}
/**
* 檢查第n個皇后是否與前面擺放的皇后衝突
* @param n
* @return
*/
public boolean check(int n) {
//檢查第n層之前的皇后位置
for (int i = 0; i < n; i++) {
// arr[i] == arr[n] 檢查是否同一列
// Math.abs(n - i) == Math.abs(arr[n] - arr[i]) 檢查是否同一斜線
if (arr[i] == arr[n] ||
Math.abs(n - i) == Math.abs(arr[n] - arr[i])) {
return false;
}
}
return true;
}
/**
* 展示某一擺法中八皇后的擺放位置
*/
public void show() {
for (int i : arr) {
System.out.print(i + " ");
}
System.out.println();
}
}
~~~