論文為：Product-based Neural Networks for User Response Prediction 

1、原理

給大家舉例一個直觀的場景：比如現在有一個鳳凰網站，網站上面有一個迪斯尼廣告，那我們現在想知道使用者進入這個網站之後會不會有興趣點選這個廣告，類似這種使用者點選率預測在資訊檢索領域就是一個非常核心的問題。普遍的做法就是通過不同的域來描述這個事件然後預測使用者的點選行為，而這個域可以有很多。那麼什麼樣的使用者會點選這個廣告呢？我們可能猜想：目前在上海的年輕的使用者可能會有需求，如果今天是週五，看到這個廣告，可能會點選這個廣告為週末做活動參考。那可能的特徵會是：[Weekday=Friday, occupation=Student, City=Shanghai]，當這些特徵同時出現時，我們認為這個使用者點選這個迪斯尼廣告的概率會比較大。

 傳統的做法是應用One-Hot Binary的編碼方式去處理這類資料，例如現在有三個域的資料X=[Weekday=Wednesday, Gender=Male, City=Shanghai],其中 Weekday有7個取值，我們就把它編譯為7維的二進位制向量，其中只有Wednesday是1，其他都是0，因為它只有一個特徵值；Gender有兩維，其中一維是1；如果有一萬個城市的話，那City就有一萬維，只有上海這個取值是1，其他是0。

那最終就會得到一個高維稀疏向量。但是這個資料集不能直接用神經網路訓練：如果直接用One-Hot Binary進行編碼，那輸入特徵至少有一百萬，第一層至少需要500個節點，那麼第一層我們就需要訓練5億個引數，那就需要20億或是50億的資料集，而要獲得如此大的資料集基本上是很困難的事情。

FM、FNN以及PNN模型

因為上述原因，我們需要將非常大的特徵向量嵌入到低維向量空間中來減小模型複雜度，而FM（Factorisation machine）——最有效的embedding model：

第一部分仍然為Logistic Regression，第二部分是通過兩兩向量之間的點積來判斷特徵向量之間和目標變數之間的關係。比如上述的迪斯尼廣告，occupation=Student和City=Shanghai這兩個向量之間的角度應該小於90，它們之間的點積應該大於0，說明和迪斯尼廣告的點選率是正相關的。這種演算法在推薦系統領域應用比較廣泛。

那我們就基於這個模型來考慮神經網路模型，其實這個模型本質上就是一個三層網路：

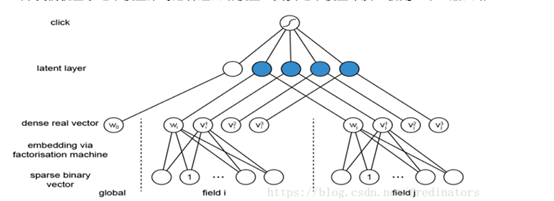
它在第二層對向量做了乘積處理（比如上圖藍色節點直接為兩個向量乘積，其連線邊上沒有引數需要學習），每個field都只會被對映到一個low-dimensional vector，field和field之間沒有相互影響，那麼第一層就被大量降維，之後就可以在此基礎上應用神經網路模型。

我們用FM演算法對底層field進行embeddding，在此基礎上面建模就是FNN(Factorisation-machinesupported Neural Networks)模型:

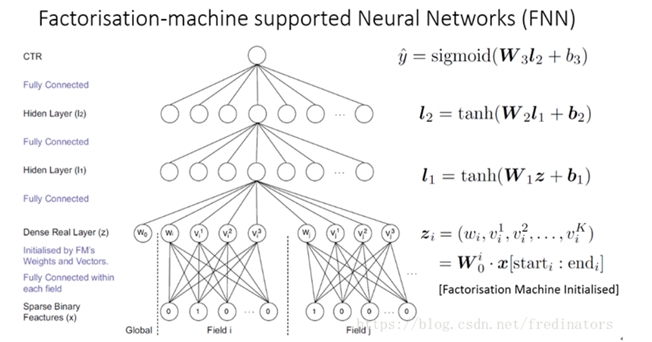
我們進一步考慮FNN與一般的神經網路的區別是什麼？大部分的神經網路模型對向量之間的處理都是採用加法操作，而FM 則是通過向量之間的乘法來衡量兩者之間的關係。我們知道乘法關係其實相當於邏輯“且”的關係，拿上述例子來說，只有特徵是學生而且在上海的人才有更大的概率去點選迪斯尼廣告。但是加法僅相當於邏輯中“或”的關係，顯然“且”比“或”更能嚴格區分目標變數。

所以我們接下來的工作就是對乘法關係建模。可以對兩個向量做內積和外積的乘法操作：

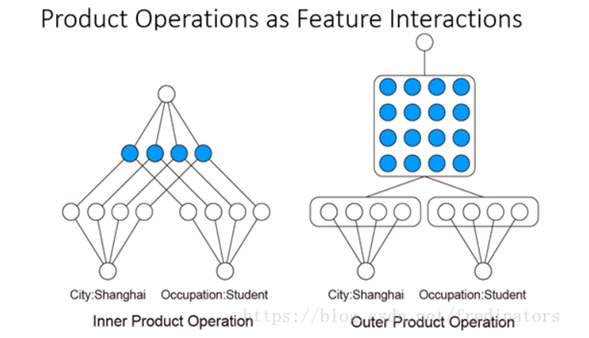
可以看出對外積操作得到矩陣而言，如果該矩陣只有對角線上有值，就變成了內積操作的結果，所以內積操作可以看作是外積操作的一種特殊情況。通過這種方式，我們就可以衡量兩個不同域之間的關係。

在此基礎之上我們搭建的神經網路PNN：

PNN，全稱為Product-based Neural Network，認為在embedding輸入到MLP之後學習的交叉特徵表達並不充分，提出了一種product layer的思想，既基於乘法的運算來體現特徵交叉的DNN網路結構，如下圖：

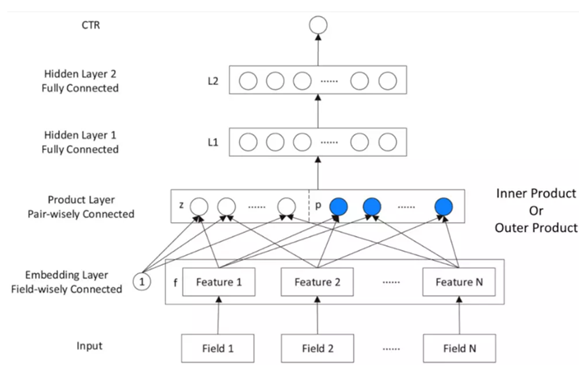
按照論文的思路，從上往下來看這個網路結構：

輸出層
輸出層很簡單，將上一層的網路輸出通過一個全連結層，經過sigmoid函式轉換後對映到(0,1)的區間中，得到我們的點選率的預測值：

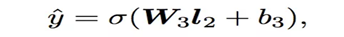
l2層

根據l1層的輸出，經一個全連結層 ，並使用relu進行啟用，得到我們l2的輸出結果：

l1層
l1層的輸出由如下的公式計算：

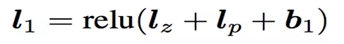
重點馬上就要來了，我們可以看到在得到l1層輸出時，我們輸入了三部分，分別是lz，lp 和 b1，b1是我們的偏置項，這裡可以先不管。lz和lp的計算就是PNN的精華所在了。我們慢慢道來:

Product Layer

product思想來源於，在ctr預估中，認為特徵之間的關係更多是一種and“且”的關係，而非add"或”的關係。例如，性別為男且喜歡遊戲的人群，比起性別男和喜歡遊戲的人群，前者的組合比後者更能體現特徵交叉的意義。

product layer可以分成兩個部分，一部分是線性部分lz，一部分是非線性部分lp。二者的形式如下：

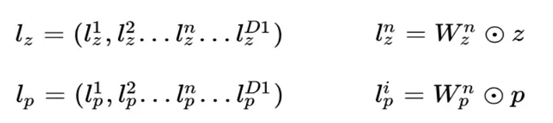
在這裡，我們要使用到論文中所定義的一種運算方式，其實就是矩陣的點乘:

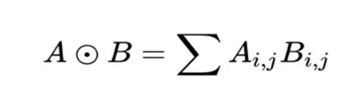
我們先繼續介紹網路結構，有關Product Layer的更詳細的介紹，我們在下一章中介紹。

Embedding Layer

Embedding Layer跟DeepFM中相同，將每一個field的特徵轉換成同樣長度的向量，這裡用f來表示。

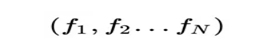
損失函式
損失函式使用交叉熵：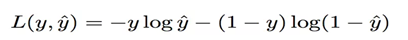

2、Product Layer詳細介紹

前面提到了，product layer可以分成兩個部分，一部分是線性部分lz，一部分是非線性部分lp。它們同維度，其具體形式如下：

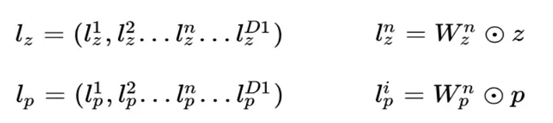
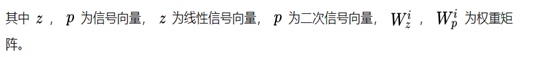
看上面的公式，我們首先需要知道z和p，這都是由我們的embedding層得到的，其中z是線性訊號向量，因此我們直接用embedding層得到：

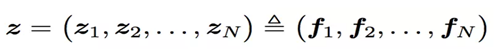
論文中使用的等號加一個三角形，其實就是相等的意思，可以認為z就是embedding層的複製。

對於p來說，這裡需要一個公式進行對映：

不同的g的選擇使得我們有了兩種PNN的計算方法，一種叫做Inner PNN，簡稱IPNN，一種叫做Outer PNN，簡稱OPNN。

接下來，我們分別來具體介紹這兩種形式的PNN模型，由於涉及到複雜度的分析，所以我們這裡先定義Embedding的大小為M，field的大小為N，而lz和lp的長度為D1。

2.1 IPNN

IPNN中p的計算方式如下，即使用內積來代表pij：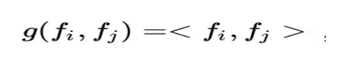

所以，pij其實是一個數，得到一個pij的時間複雜度為M，p的大小為N*N，因此計算得到p的時間複雜度為N*N*M。而再由p得到lp的時間複雜度是N*N*D1。因此 對於IPNN來說，總的時間複雜度為N*N(D1+M)。文章對這一結構進行了優化，可以看到，我們的p是一個對稱矩陣，因此我們的權重也可以是一個對稱矩陣，對稱矩陣就可以進行如下的分解：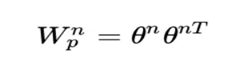

因此：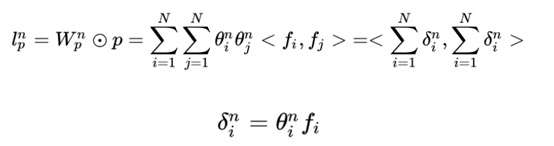

因此：

2.2 OPNN

OPNN中p的計算方式如下：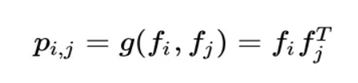

此時pij為M*M的矩陣，計算一個pij的時間複雜度為M*M，而p是N*N*M*M的矩陣，因此計算p的事件複雜度為N*N*M*M。從而計算lp的時間複雜度變為D1 * N*N*M*M。這個顯然代價很高的。為了減少複雜度，論文使用了疊加的思想，它重新定義了p矩陣：

通過元素相乘的疊加，也就是先疊加N個field的Embedding向量，然後做乘法，可以大幅減少時間複雜度，定義p為：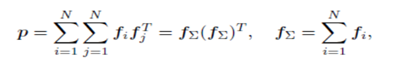

這裡計算p的時間複雜度變為了D1*M*(M+N)

3.Discussion

和FNN相比，PNN多了一個product層，和FM相比，PNN多了隱層，並且輸出不是簡單的疊加；在訓練部分，可以單獨訓練FNN或者FM部分作為初始化，然後BP演算法應用整個網路，那麼至少效果不會差於FNN和FM；

三、EXPERIMENTS

使用Criteo和iPinYou的資料集，並用SGD演算法比較了7種模型：LR、FM、FNN、CCPM、IPNN、OPNN、PNN（拼接內積和外積層），正則化部分（L2和Dropout）；

實驗結果如下圖所示：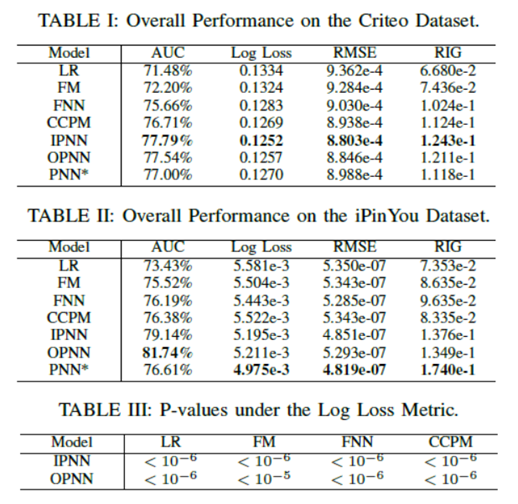

結果表明PNN提升還是蠻大的；這裡介紹一下關於啟用函式的選擇問題，作者進行了對比如下：

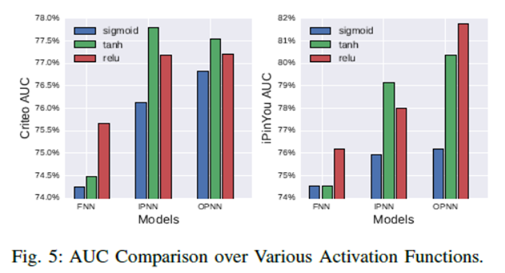
從圖中看出，好像tanh在某些方面要優於relu，但作者採用的是relu，relu的作用： 1、稀疏的啟用函式（負數會被丟失）；2、有效的梯度傳播（緩解梯度消失和梯度爆炸）；3、有效的計算（僅有加法、乘法、比較操作）；

參考：

1.https://www.jianshu.com/p/be784ab4abc2

2.https://blog.csdn.net/buwei0239/article/details/86755998

3.https://blog.csdn.net/fredinators/article/details/79757629

4.https://zhuanlan.zhihu.com/p/33177517

&n