目錄

1、前述

2、向量空間的梯度下降：

3、函式空間的梯度下降：

4、梯度下降的流程：

5、在向量空間的梯度下降和在函式空間的梯度下降有什麼區別呢？

6、我們看下GBDT的流程圖解：

7、我們看一個GBDT的例子：

8、我們看下GBDT不同版本的理解：

1、前述

從本課時開始，我們講解一個新的整合學習演算法，GBDT。

首先我們回顧下有監督學習。假定有N個訓練樣本， ， 找到一個函式 F(x)，對應一種對映使得損失函式最小。即：

如何保證最小呢？就是通過我們解函式最優化的演算法去使得最小，常見的有梯度下降這種方式。

2、向量空間的梯度下降：

我們想想在梯度下降的時候，更新w是怎麼更新的呢，先是隨機找到一個w0，然後舉根據梯度下降的迭代公式：     

詳細解釋下這個公式，其中

意思是把損失函式先對w進行求導，得到一個導函式，或者說得到一組導函式，因為w是多元函式，得到了一組導函式之後，再把Wn-1這一組w帶進去，得到一組值，這組值我們稱作梯度，把梯度加個負號就是負梯度，乘一個λ是學習率。 這個公式整體的意思是 我只要把w加上一個L對於w的負梯度，把 作為∆w，加到原來的w上，新產生出來的w就是比原來的w要好一些，能讓損失函式更小一些，這就是對於w引數的一個提升。所以接下來我們的迭代步驟就是w1=w0+△w0，w2=w1+△w1=w0+△w0+△w1，這裡是把w2用w1表示出來。w3=w2+△w2=w0+△w0+△w1+△w2，....所以最終的wn可以表達為wn=w0+△w1+△w2+...+△w(n-1)。一般情況下我們初始的時候w0=0。所以最後可以表達為

這就是向量空間的梯度下降的過程。所謂向量空間的梯度下降，為什麼叫做向量空間的梯度下降，因為w是一組向量，我們是在w上給它往下降所以稱為向量空間的梯度下降。

3、函式空間的梯度下降：

這裡面的F*在假如邏輯迴歸裡面就是1/1+e^-z。在其他演算法裡各自對應其損失函式。對於決策樹來說，樹其實也是有損失函式的，比如我們之前在後剪枝的時候，通常做法就是，拿測試集或者驗證集去檢驗一下我cancel掉葉子節點會不會變好一點，但實際上還有另一種減枝方式，就是根據損失函式來的，別管損失函式是什麼，它是一個L，L跟x有關的，跟葉子節點的數量T有關，表達為L (x,T)。T相當於一個正則項，葉子節點算的數量越多，它的損失函式就越大，它不想讓樹太複雜了，通過剪枝剪一次去去看損失函式，是上升了還是下降了，如果損失函式下降了，剪枝就承認它，以後就都不要節點了，所以說對於決策樹本身是可以定義一個損失函式的，只不過定義出來它意義不大，只能在剪枝的時候看看用來效果怎麼樣，因為我們知道損失函式是用來評估結果的，評估你的模型到底怎麼樣的，那我們剪枝的時候拿它進行一個評估也是一個比較科學的方法，但是訓練的過程中是用不到損失函式，因為你不知道怎麼分裂可以影響到損失函式，所以訓練的時候基本都沒有提損失函式，而是用基尼係數，資訊熵這種變通的方式。另一方面，樹的損失函式也不能直接使用梯度下降來下降這個損失函式，按原來的做法我們有一堆w把空先給你留好了，然後你找到一組最好的w讓損失函式最小就可以了，但樹按照這個思路怎麼來呢，應該是找到所有可能性的樹，挑出一個能使損失函式最小的樹，按理說應該這麼做，但是這麼做不現實，因為樹有無窮多個，所以我們採用其它方式得到一個近似最好的可能性。所以對與單純的決策樹我們一般不適用損失函式。

但是一旦變成了整合學習，我們又可以把損失函式又讓它重出江湖了。對於決策樹我們不能使用梯度下降的方式，因為在決策樹裡面損失函式就像一個黑盒，沒有具體的引數通過損失函式供我們優化。但是對於整合學習則可以使用，因為整合學習對應著很多樹。首先決策樹是根據選取的特定條件由根節點開始逐級分裂，直到滿足純度要求或達到預剪枝設定的停止而形成的一種樹。那如何選取特定條件? 常見的有：GINI係數， Entropy，最小二乘MSE。而回歸樹就是每次分裂後計算分裂出的節點的平均值， 將平均值帶入MSE損失函式進行評估。而GBDT是一種決策樹的提升演算法 ，通過全部樣本迭代生成多棵迴歸樹， 用來解決迴歸預測問題(迭代生成的每棵樹都是迴歸樹)，通過調整目標函式也可以解決分類問題。傳統的迴歸問題損失函式是：

yi是真實的樣本的結果，y^是預測的結果。而在整合學習裡面，y^就是我們每一次的預測的G(x)，所以現在我們的損失函式變成yi和大G(x)的一個損失函數了，因此整合學習裡面損失函式表示式為L=L(yi，G)。我雖然不能寫出來具體的損失函式，但是肯定是關於yi和G的一個表示式，我想找到一個最好的大G(x)，一步去找，找不到，怎麼辦，我就分步去找，最開始找到一個G0(x)，它一般不是能讓損失函式最小的，我知道有梯度下降這個工具，能讓它更接近損失函式最低點一些。我們希望損失函式下降，希望每一次能找到一個新的G(x)，就像向量空間梯度下降中更新w一樣，我們希望找到一個新的w，w是損失函式改變的原因，現在變成了每一次的G(x)是損失函式改變的原因，每一次的G(x)的改變一定會改變損失函式，G(x)只要它能改變損失函式，損失函式不是上升就是下降。怎麼著能讓它損失函式降低呢？我們知道最終的G(x)是一堆g(x)相加，換一個角度來講，第一步迭代我們得到了一個G1(x)=g1(x)，第二步迭代我們得到了G2(x)=G1(x)+g2(x)，第三步就是G3(x)=G2(x)+g3(x)，注意這個形式，整合樹的每一步迭代形式和梯度下降每一步的迭代形式似乎很像，我們注意觀察，在梯度下降裡，每一步迭代所要加的△w只要是前一項的值帶到損失函式裡面的負梯度 ，就可以讓損失函式變得更小。而我現在所謂的整合學習一輪一輪的迭代，第一輪我想加上一個g1(x)，第二輪我想再加上g2(x)，第三輪我想再加上g3(x)，根據梯度下降的原則，加上的每一個g(x)等於什麼的時候能夠讓整合學習的損失函式越來越小呢？能不能也讓它等於損失函式對於上一次的預測整體的結果G(x)這個東西的負梯度？這樣損失函式一定會也是下降的。我把G(x)當做一個整體來看待，類似於原先的w變數。反正都是讓損失函式改變的原因。這種梯度下降的過程就稱為函式空間的梯度下降過程。函式空間的梯度下降是什麼意思呢？因為在函式空間中這個函式它寫不出來是由什麼w組成的，它的最小單位就是這個弱分類器本身，所以我們只能在函式空間進行梯度下降。

最開始不管用什麼方法，已經得到了第一代G0(x)，這時能算出來損失函式，它是能讓損失函式結果最小的那個G(x)嗎？應該不是。我們希望把它修改修改，讓它變好一些，能讓損失函式降低。我令G1(x)=G0(x)加上損失函式對於G0的負梯度，即             

即G1(x)=G0(x)+∆G0，此時的G1(x)就能比G(x)讓損失函式變得更低一些了。然後依次G2(x)去迭代。G2(x)=G1(X)+∆G1，∆Gt應該等於損失函式L對於Gt的梯度，即

只要每次加上的都是∆Gt這麼個東西，每一步帶入各自的∆Gt，第一次帶入∆G0，第二次帶入∆G1，以此類推，就能保證最後得到的G一次比一次的能夠讓損失函式變小。一直到GT(X)=GT-1(X)+∆GT-1。此時GT(X)就是我們最終要得到的GT(X)。表達如下：

這裡面每一步的所加的∆G不就是整合學習裡邊每一步加的弱分類器g(x)嗎，第一次你希望加上一個g1(x)，第二次加上一個g2(x)，一直加到gt(x)，最終的大Gt(x)等於什麼呢，假設G0(x)=g0(x)=0，Gt(x)=g0(x)+g1(x)+g2(x)……一直加到gt-1(x)，這不就是一個另一個視角看的整合學習嘛。對於最小二乘損失函式來說，損失函式是：

對y^求偏導就是2(y-y^)，通常在前面還有個學習率，假如學習率是1/2的話那麼會和2相乘抵消，所以最後的求導結果是y-y^，對於我們的整合學習來說y^就是上一步的整體的預測結果Gt-1(x)。所以整合學習的損失函式對G(x)的求導結果就是：

所以在t輪我們應該訓練出的gt(x)的預測結果應該等於 。對於決策樹演算法來說的話，即為以 為新的標籤,x為feature,擬合一顆新的決策樹。通過這種方式，來訓練的G(x)，就叫做GBDT。

4、梯度下降的流程：

說了這麼多，到底什麼是梯度下降？所謂梯度下降，也就是對於任何一個函式來說，只要這個函式是個凸函式，它的自變數是x，也就是說這個函式受x改變而改變，你只要瞎蒙出來一代x，你接下來不停的去迭代，每次迭代的準則就是加上一個函式對上一代自變數的求導，即負梯度，表達為xn=xo-∂F/∂x ，這麼不停的迭代，最終得到的x就能夠找到F(x)的最小值，這個東西就叫做梯度下降。

梯度下降和L-BFGS一樣，它就是一個演算法，一個函式關於一個變數的演算法。每次我就讓這個函式加上關於自變數的負梯度，就能讓函式越來越小。所以我不限制這個變數到底是w還是G，只要你這個東西能真真切切地影響我的大小，我去求你的負梯度，就能讓你越降越低。這就是隨機梯度下降演算法的過程。它是不挑食的。

你優化的內容就是你去調整的內容，在函式性模型裡，真真正正影響損失函式大小的是w，所以我去調整w，讓w始終朝著負梯度的方向去改變，最終就能讓損失函式降到最低。而在帶著樹的整合學習裡面，最小的能夠調整的單位沒有w了，你只能調整你加進來那棵小樹，所以你就去優化這棵小樹，讓你新加進來的小樹的預測結果儘量等於函式空間上的負梯度方向。

其實它比向量空間的梯度下降的運算量至少是要少的，為什麼呢？因為在向量空間中，w是一個向量，它要求一系列偏導，而在函式空間的梯度下降中，此時的變數就是一個數，所以就是一個求導數的概念了，也就是一維空間的梯度下降，每次加上一個數。

5、在向量空間的梯度下降和在函式空間的梯度下降有什麼區別呢？

​

詳細解釋下：

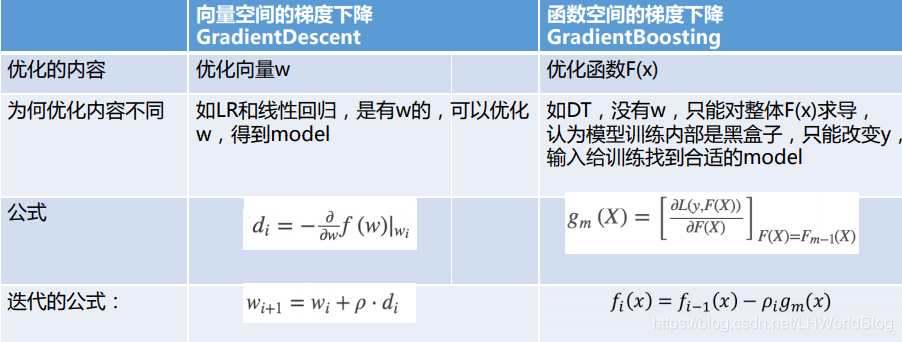
首先向量空間的梯度下降，翻譯是GradientDescent，函式空間的梯度下降，翻譯是GradientBoosting，說明是用在Boosting裡面的。其次向量空間的梯度下降優化內容是w，而函式空間優化函式F(x) ，為什麼優化內容不同，向量空間如LR和線性迴歸，是有w的，可以優化w，得到model。而函式空間中，如DT，沒有w，只能對整體F(x)求導， 認為模型訓練內部是黑盒子 只能改變預測值 y^， 輸入給訓練找到合適的model。向量空間中是對w求導，即

而函式空間是直接對整體F(x)求導，即

這裡面直接對F(x)求導，並且把上一代的F(x)值給帶進去。迭代公式也發生了變化。

向量空間中是 ，函式空間中是 。

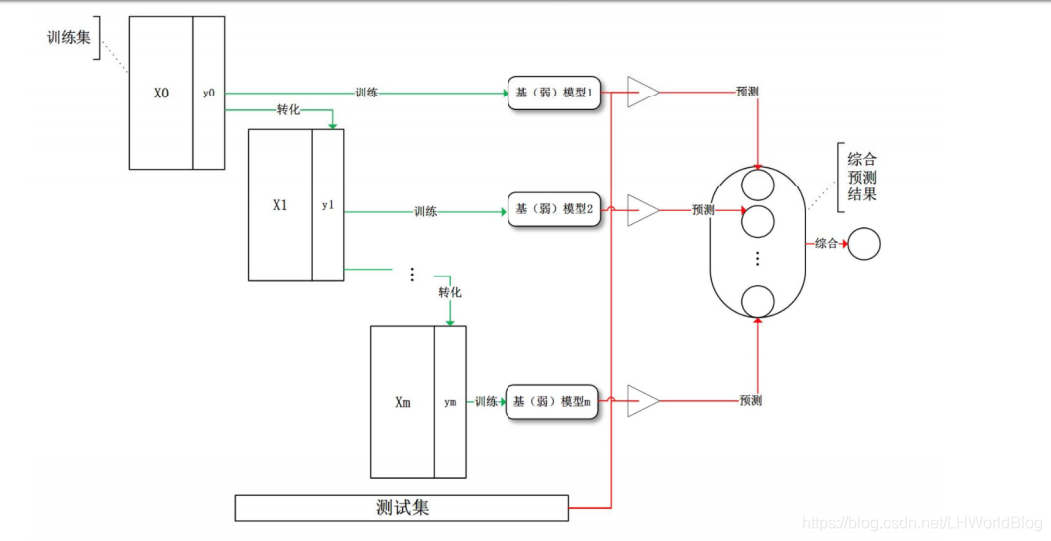
6、我們看下GBDT的流程圖解：

​

解釋下上面流程：

首先訓練集x0和y0，我在原始的訓練集上訓練一個比較弱的決策樹，長成了一棵樹。這是第一個模型1。通過預測的結果把訓練集上的標籤轉化為X1，Y1。原來Adaboost是改變資料的權重，現在GBDT是改變Y的標籤，然後再訓練第二個模型，再改變標籤。反覆迭代下去，將所有的預測結果綜合作為最後的預測結果，這就是GBDT的流程。

7、我們看一個GBDT的例子：

​

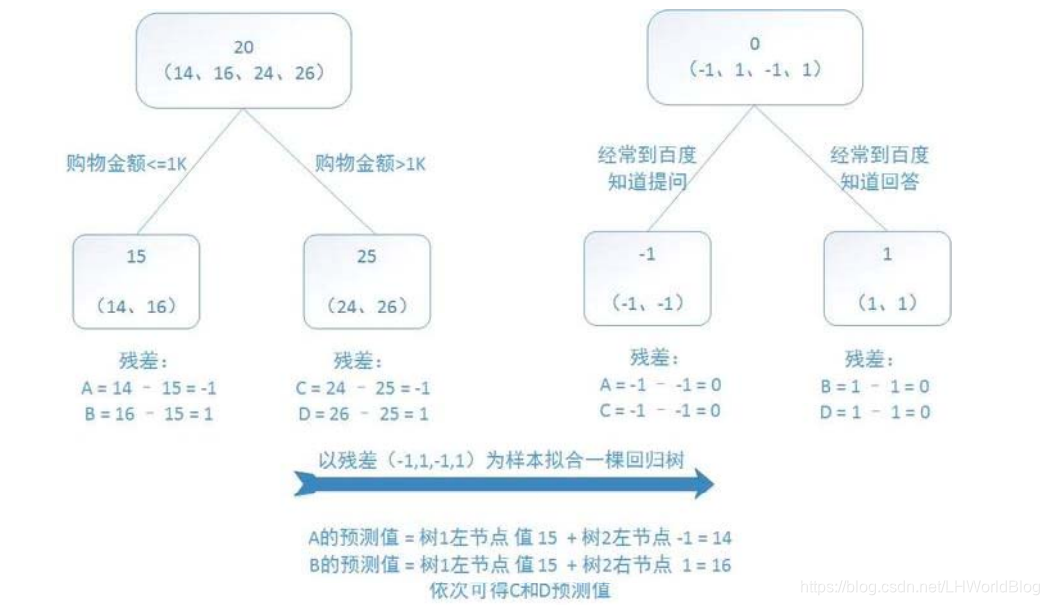
假如用購物金額和是否經常去百度知道提問這兩個條件作為x去判斷這個人的年齡，訓練的時候我有四條資料，分別是14歲，16歲，24歲和26歲。

我上來想訓練出一棵迴歸樹來，在根節點的時候平均值是20。接下來回歸樹怎麼訓練？拿什麼評估引數？拿mse，抱得最緊的放到一起。此時給它一分為二，我發現購物金額小於等於1000和大於1000，能夠把14，16分到左邊，24和26分到右邊。這個樹我人為的限制它只允許你有兩層。現在左邊這個節點輸出的結果通通是15，假如4條樣本資料分別對應編號是A,B,C,D的話，此時y^A，y^B等於15，y^C，y^D 等於25。

此時y^與真實的y之間有沒有殘差？有殘差，我們知道負梯度就是殘差。接下來我想訓練第二棵樹，第二棵樹希望輸出結果是負梯度，也就是我希望輸出結果是殘差。那麼我就想要把殘差當做label放回到原來去，那麼對於這四條資料，它們的y原來是14,16,24,26，咱現在就變成-1，+1，-1，+1 。怎麼來的？本來是14，預測成了15，y- y^等於-1；那麼原來是24變成25了，它也是-1。

接下來我再根據經常到百度提問作為條件進行一次分類，迴歸樹是不管你的label的，我就想把最接近的給湊到一起去，所以接下來就把兩個-1湊到一起了，把兩個+1湊到一起了。那麼第二代的y^A就等於-1，y^B等於1。因為這兩個1分到一起，它們平均值也是1就預測準了。 y^C等於-1，y^D 等於+1。

現在兩棵樹訓練完了，最終我們來一條資料，比如說來一條資料14，它要怎麼來做預測？把它丟到第一個樹裡面，得到一個15；再丟到第二棵樹裡面，得到一個-1，最終的G=15-1=14，得到一個正確的預測結果。

8、我們看下GBDT不同版本的理解：

GBDT直觀的來看，就是說比如這個人90歲，第一個數給它預測成了78歲，還剩12歲，第二棵樹就把12歲作為標準預測，結果它只預測到了十歲，還差兩歲。第三個樹又根據兩歲作為標準，此時再次預測為1.5，第四個樹根據0.5作為標準預測結果為0.5，最後四棵數加到一起正好是90，每次擬合的都是殘差，這是簡單版的理解GBDT的過程。

核心版的理解是為什麼每次要預測殘差，因為對於迴歸問題來講，剛好負梯度等於殘差，所以去預測的是殘差。因為你的mse帶著平方求導就是殘差。通常F(x)在相加的時候，會給這殘差也乘一個縮水的學習率，比如0.1。第二次雖然預測出12，我只給你加上1.2，防止你走過了，下次從78就變成79.2了，還差一大截的，你第三個再照樣去努力預測，再給乘一個縮水系數，跟咱們的梯度下降的學習率是一模一樣的。

這個實際上是原始的GBDT應對迴歸問題的時候，可以使用簡單的把y level做一個替換，去重新訓練的這麼一種方式。但是對於分類問題，它就不好使了，所以xgboost提供了一個最終版的解決方