嘟嘟在上兩個文章裡面簡單粗糙的講了講關於MySql儲存引擎的一些特性以及選擇。個人感覺如果面試官給我機會的話，至少能說個10分鐘了吧。只可惜有時候生活就是這樣：骨感的皮包骨頭了還在那美呢。牢騷兩句，北京的夏天真的是熱的膠粘。昨天上班兒忙到了晚上11點多，本想著昨兒晚上就把關於資料庫優化的文章寫完了，今天就能寫個關於高併發的。結果嘟嘟這個小屋子就好比那商務大洗浴的汗蒸房一樣。嘟嘟昨夜屬實有點暈乎。只好晚上鍛鍊鍛鍊身體之後看了一集《長安十二時辰》。。。。。話不多說，今天學學關於索引的一些問題。

　　索引簡介

　　優點

　（索引可以大大大大大大的提高查詢效能！）

　　1.通過建立唯一性索引，保證資料庫每一行資料的唯一性

　　2.大大加快檢索速度

　　3.加速表和表之間的連線

　　4.減少查詢中分組和排序的時間

　　5.通過使用索引，在查詢的過程中，使用查詢優化器，提高系統性能

　　缺點

　　1.建立索引和維護索引消耗時間，這種時間隨資料量增加而增加

　　2.索引需要佔用物理空間，如果建立聚簇索引，佔用空間更大

　　3.如果表中增刪改，索引需要動態維護，降低資料的維護速度

　　什麼欄位適合建立索引

　　1.常搜尋的列上，加快搜索速度

　　2.主鍵列上（MySql 在主鍵上面預設增加索引）

　　3.常用的連線列上（外來鍵），加快連線速度

　　4.在經常根據範圍進行搜尋的列上建立索引，因為索引已經排序，其指定範圍是連續的 （a between xxx and xxx  但是不是    in   （5，10，15）這種）可以在a上面加上索引

　　5.經常需要排序的列上建立索引，因為索引已經排序，這樣查詢可以利用索引的排序，加速查詢時間

　　6.經常使用where子句中的列上建立索引，加快條件的判斷速度

　　需要注意的一點是 ：比如在 where f1。。。 and f2。。。，那麼我們在欄位f1或者f2上建立索引是沒有用的，只有在f1和f2上同時建立索引才有用

　　什麼樣的欄位不適合建立索引

　　1.查詢中很少使用到的，或者參考的列就沒必要加索引

　　2.資料值相對少的列也不適合。舉個極端點的栗子：people 欄位有20萬條。sex 欄位有三條（男，女，不男不女） 在sex欄位上面新增索引就是沒有用的

　　3.大文字資料不應該增加索引。

　　4.經常增刪改，但是查詢比較少的時候就不需要做索引啦

　　停停停停！因為索引的具體介紹涉及到了關於查詢機制（怎麼查詢一個東西更快的方法）的一些問題，所以嘟嘟先在這裡惡補一下查詢的相關機制，便於後面繼續學習索引種類。

　　1.樹是什麼玩應？（B-Tree ，這 Tree 那Tree的）

　　首先一棵小樹，必須先有一個根，然後依靠這個根來開枝散葉。就形成了一棵樹。

　　  2.怎麼查詢快？

　　設想一下，如果在查詢一大堆資料的過程中，我們能依靠某些辦法，去捨棄一些沒有必要去查詢的東西。那麼查詢的速度就會比一個一個查的速度快的多。

　　  基於以上兩點，網上給大家扒下來一棵能夠讓我們查詢資料時候快一些的樹

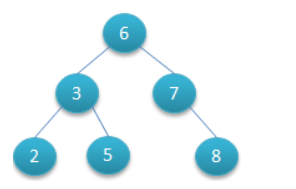
　　　　6那個地方是根， 258 是葉子，37是分支，235678的值叫做鍵值

　　   1. 這棵樹的形成是有一定的規則的：

　　　根的左邊（235）叫做左子樹，根的右邊（78）叫做右子樹，首先第一個規則就是右子樹的鍵值要大於根鍵值，左子樹相反。

　　   2. 給定的這6個數字235678為什麼就把根選成6了？因為6是中間數，至於為什麼不是5？嘟嘟個人覺得也可以，就這麼畫唄：

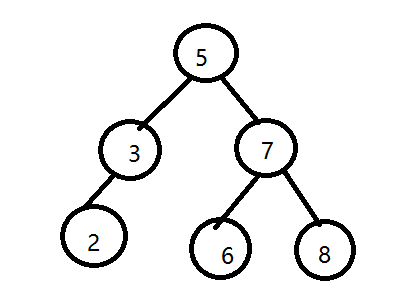
　　3.我們把每一個數值對應的那個點叫做節點。那麼我這棵樹也滿足上邊的那個規則：相對於每一個節點，他左側的子節點都會比他小，右側的子節點都會比他大。

　　4.這麼做有什麼好處呢？用嘟嘟自己畫的那張圖為例子奧，比如嘟嘟要查6這個數字需要查幾次？（1）先查到了5，發現6比5大 ，根據規則，往右側走到了7。（2）發現6比7小根據規則往左側走到了6！查完了。用了兩步。那麼正常按照順序查詢的話，就不一定查多少次了。

　　5.那麼6個隨機數字，在我們按照上述規則進行排序之後想要查詢一個數字，需要查詢多少次？（1）查詢第一個數字5需要一步.（2）查詢第二層數字3或者7需要2次並且有兩種可能，意思是你想查3需要兩次，你想查7也得需要兩次。（3） 同理，在查詢第三層的數字的時候3種可能，並且第三層的任意數字你都需要查三次。所以平均下來就是：

　　（1+2+2+3+3+3）/（1+2+3）=2.3次平均

　　 相比正常排序的查詢（1+2+3+4+5+6）/6=3.5次  查詢確實快了一些。原因就是通過比大小的方式，將一些沒有必要查詢的數字給捨棄了。

　　6.聽說這種樹叫做二叉樹。而二叉樹也有別的畫法：

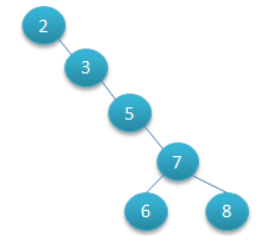
　　（很明顯這種數的查詢效率就底下） （1+2+3+4+5+5）/6=3.3次

　　針對上面那個效率低下的二叉樹，就又引入一條規則，進而產生了一種平衡二叉樹（AVL Tree）

　　1.這條規則就是，對於任何一個節點下面的兩個子樹的高度差都<=1

　　  嘟嘟個人推測這種平衡的機制可以保證搜尋效率的最大化（因為嘟嘟時間有限，這個結論是看上面三顆樹對比之下的效率感覺的）

　　  2.如果在一棵已經平衡的樹上面增加一個數，減少一個數，或者修改一個數，樹的平衡就可能被打破了（嘿嘿嘿，嘟嘟想起來文章開頭寫的，如果某些欄位經常發生增刪改就不太適合使用索引，因為平衡機制被打破了得話，就得重新耗費資源區重構這種平衡）。

　　  3.如果平衡被打破，需要重構（通過一種叫做旋轉的辦法保證二叉樹的平衡，詳細的流程嘟嘟推薦大家看看別的部落格），旋轉的方式嘟嘟在這裡就不再贅述了，意思就是通過位置的調換，保證二叉樹的原則就是了。

　　B-Tree（平衡多路查詢樹）

　　1.B-Tree 是針對磁碟等外儲存裝置設計的一種平衡查詢樹

　　  2.為什麼會出現B-Tree 這種查詢機制呢？ 因為InnoDB  儲存引擎，InnoDB管理磁碟的最小單位是頁（16KB），而磁碟儲存資料的最小單位是磁碟塊block（遠遠小於16KB），這就造成了，InnoDB在進行資料讀取（比如查詢的時候）會將連續的好幾個磁碟塊讀入（老子必須讀夠16KB！）。這是個硬傷。因為讀取也是浪費資源的。而InnoDB你一次讀的太多了。

　　  3.針對2中讀的太多的問題。如果有一種查詢機制可以繼續減少查詢的時候IO的次數，就會降低資源的浪費。

　　  4.B-Tree誕生了。

　　下面這張圖片能夠比較完美的詮釋B-Tree的特性

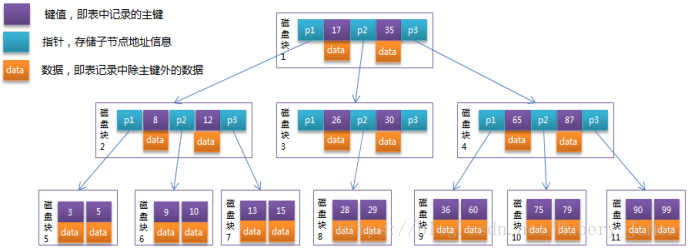
　   嘟嘟在別的哥哥的部落格上扒下來的圖片。第一眼看的時候可能是因為天氣太熱，有點暈乎。但是睡一覺起床以後再看它（MD豁然開朗）

　　 1.首先每一個磁碟塊都是一個節點,每個節點都有三個指標兩條資料。

　　 2.資料都是以【key,data】的方式儲存的。每條指標都儲存子節點的地址。兩條資料的key值是從小到大排序。

　　 3.於是乎以磁碟塊1為例子，就形成了三個區間 {小於17的，17至35的，35以上的}，並分別有不同的指標指向對應的磁碟塊。

　　 4.對比平衡二叉樹的話，在單次的選擇上，二叉樹只能選擇出到底我要查詢的數是比現在大還是比現在小（也就是2選1），而B-Tree每一次可以選擇出來我要查的數具體在哪個區間（多選一），導向更加精確，自然查詢次數會更少。

　　關於索引和查詢的相關介紹。嘟嘟就講到這裡啦，下次嘟嘟會繼續學習關於具體索引的知識。以上寫的東西嘟嘟基本上是粗淺理解了一下然後現學現賣。畢竟嘟嘟是個新手，對資料結構與演算法什麼的並沒有太高的要求。但是理解一下，既為以後打下一個引子，又不至於學的腦袋疼。