影象相似度中的Hash演算法
本部落格中使用的程式碼見本文末尾
度量兩張圖片的相似度有許多演算法,本文講介紹工程領域中最常用的圖片相似度演算法之一——Hash演算法。Hash演算法準確的說有三種,分別為平均雜湊演算法(aHash)、感知雜湊演算法你(pHash)和差異哈雜湊演算法(dHash)。
三種Hash演算法都是通過獲取圖片的hash值,再比較兩張圖片hash值的漢明距離(韓明距離的概念可見本公眾號《》一文)來度量兩張圖片是否相似。兩張圖片越相似,那麼兩張圖片的hash數的漢明距離越小。下面本文將分別介紹這三種Hash演算法。
1 平均雜湊演算法(aHash)
1.1 演算法步驟
平均雜湊演算法是三種Hash演算法中最簡單的一種,它通過下面幾個步驟來獲得圖片的Hash值,這幾個步驟分別是(1) 縮放圖片;(2)轉灰度圖; (3) 算畫素均值;(4)根據相似均值計算指紋。具體演算法如下所示:
| 步驟 | 具體內容 |
|---|---|
| 縮放圖片 | 輸入圖片大小尺寸各異,為了統一圖片的輸入,統一將圖片尺寸縮放為8*8,一共得到了64個畫素點。 |
| 轉灰度圖 | 輸入圖片有些為單通道灰度圖,有些RGB三通道彩色圖,有些為RGBA四通道彩色圖。也為了統一下一步輸入標準,將非單通道圖片都轉為單通道灰度圖。 其中RGB三通道轉單通道演算法有下面幾種: 1.浮點演算法:Gray=R0.3+G0.59+B0.11 2.整數方法:Gray=(R30+G59+B11)/100 3.移位方法:Gray =(R76+G151+B*28)>>8; 4.平均值法:Gray=(R+G+B)/3; 5.僅取綠色:Gray=G; |
| 算畫素均值 | 通過上一步可得一個8x8的整數矩陣G,計算這個矩陣中所有元素的平均值,假設其值為a |
| 據畫素均值計算指紋 | 初始化輸入圖片的ahash = "" 從左到右一行一行地遍歷矩陣G每一個畫素如果第i行j列元素G(i,j) >= a,則ahash += "1"如果第i行j列元素G(i,j) <a, 則ahash += "0" |
得到圖片的ahash值後,比較兩張圖片ahash值的漢明距離,通常認為漢明距離小於10的一組圖片為相似圖片。
1.2 具體例項
本文圖片為Lena圖來說明.

圖1 Lena(Origin)圖
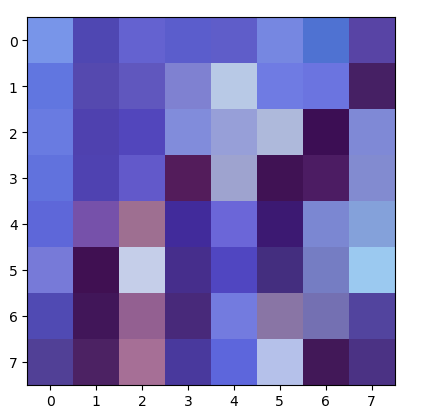
圖2 轉為8x8尺寸的Lena圖
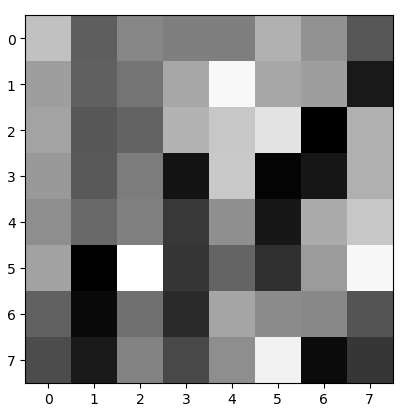
圖3 轉為灰度8x8尺寸的Lena圖
其中轉為8x8尺寸的Lena對應的資料矩陣為:
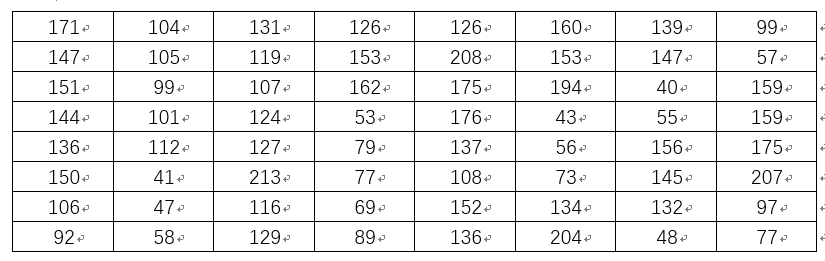
很容得到如上矩陣所有元素的均值a= 121.328125, 將上述矩陣中大於或等於a的元素置為1, 小於a的元素置為0,可得:
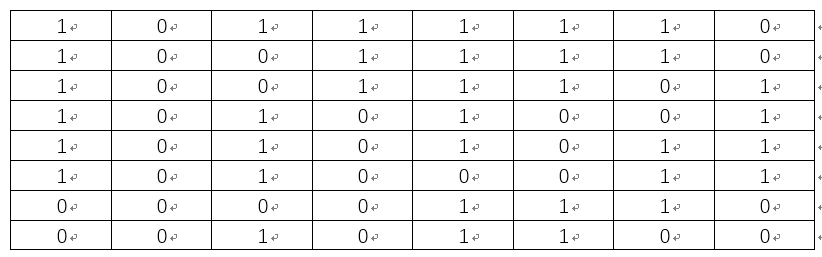
所以可得Lena圖的aHash為
1011111010011110100111011010100110101011101000110000111000101100
將二進位制形式ahash轉十六進位制hash為
be9e9da9aba30e2c
為了測試aHash演算法的效果,我們用一張帶噪聲Lena(noise)圖和與Lena不一樣的Barbara做圖片相似度對比實驗,其中Lena(noise)和Barbara如下:

圖4 Lena(noise)圖

圖5 Barbara圖
通過aHash演算法容易得三個圖片的hash值,然後根據hanming距離計算Lena(origin).png和Lena(noise).png Barbar.png之間漢明距離,具體如下:
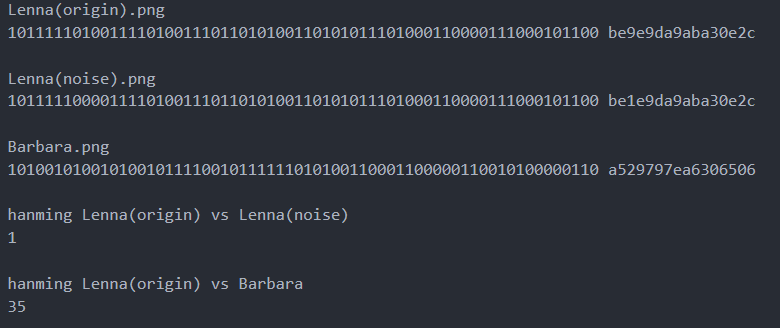
圖6 aHash演算法圖片相似度實驗
由上圖可見aHash能區別相似圖片和差異大的圖片。
2 感知雜湊演算法(pHash)
2.1 演算法步驟
感知雜湊演算法是三種Hash演算法中較為複雜的一種,它是基於DCT(離散餘弦變換)來得到圖片的hash值,其演算法幾個步驟分別是(1) 縮放圖片;(2)轉灰度圖; (3) 計算DCT;(4)縮小DCT; (5)算平均值;(6) 計算指紋。具體演算法如下所示:
| 步驟 | 具體內容 |
|---|---|
| 縮放圖片 | 統一將圖片尺寸縮放為32*32,一共得到了1024個畫素點。 |
| 轉灰度圖 | 統一下一步輸入標準,將非單通道圖片都轉為單通道灰度圖。 |
| 計算DCT | 計算32x32資料矩陣的離散餘弦變換後對應的32x32資料矩陣 |
| 縮小DCT | 取上一步得到32x32資料矩陣左上角8x8子區域 |
| 算平均值 | 通過上一步可得一個8x8的整數矩陣G, 計算這個矩陣中所有元素的平均值,假設其值為a |
| 計算指紋 | 初始化輸入圖片的phash = "" 從左到右一行一行地遍歷矩陣G每一個畫素 如果第i行j列元素G(i,j) >= a,則phash += "1" 如果第i行j列元素G(i,j) <a, 則phash += "0" |
得到圖片的phash值後,比較兩張圖片phash值的漢明距離,通常認為漢明距離小於10的一組圖片為相似圖片。
2.2 具體例項
仍用Lena圖來說明.
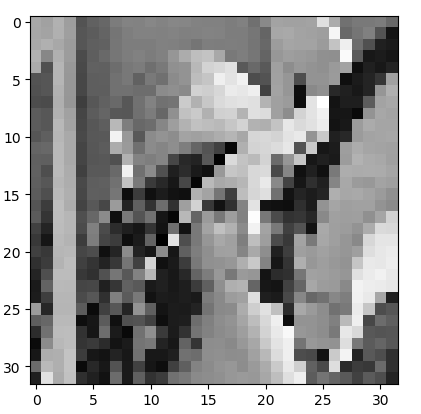
圖7 轉為灰度32x32尺寸的Lena圖

圖8 灰度32x32尺寸Lena圖對應的DCT矩陣
通過計算可得灰度32x32Lenna圖對應的DCT矩陣左上角8x8區域子矩陣為:

很容得到如上矩陣所有元素的均值a= 77.35, 將上述矩陣中大於或等於a的元素置為1, 小於a的元素置為0,可得:
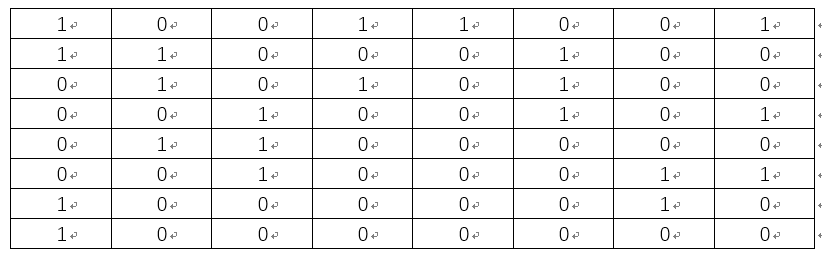
所以可得Lena圖的pHash為
1001100111000100010101000010010101100000001000111000001010000000
將二進位制形式phash轉十六進位制hash為
99c4542560238280
為了測試pHash演算法的效果,同樣用一張帶噪聲Lena(noise)圖和與Lena不一樣的Barbara做圖片相似度對比實驗。通過pHash演算法容易得三個圖片的hash值,然後根據hanming距離計算Lena(origin).png和Lena(noise).png Barbar.png之間漢明距離,具體如下:
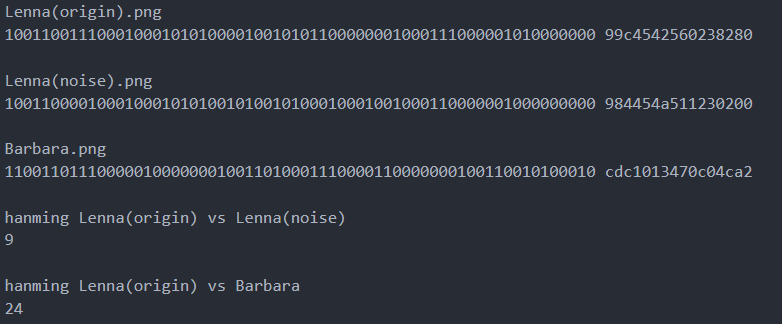
圖9 pHash演算法圖片相似度實驗
由上圖可見pHash能區別相似圖片和差異大的圖片。
3 差異雜湊演算法(dHash)
3.1 演算法步驟
相比pHash,dHash的速度要快的多,相比aHash,dHash在效率幾乎相同的情況下的效果要更好,它是基於漸變實現的。其演算法幾個步驟分別是(1) 縮放圖片;(2)轉灰度圖; (3) 計算DCT;
(4)縮小DCT; (5)算平均值;(6) 計算指紋。具體演算法如下所示:
| 步驟 | 具體內容 |
|---|---|
| 小圖片 | 統一將圖片尺寸縮放為9x8,一共得到了72個畫素點 |
| 轉灰度圖 | 統一下一步輸入標準,將非單通道圖片都轉為單通道灰度圖。 |
| 算差異值 | 當前行畫素值-前一行畫素值, 從第二到第九行共8行,又因為矩陣有8列,所以得到一個8x8差分矩陣G |
| 算平均值 | 通過上一步可得一個8x8的整數矩陣G, 計算這個矩陣中所有元素的平均值,假設其值為a |
| 計算指紋 | 初始化輸入圖片的dhash = "" 從左到右一行一行地遍歷矩陣G每一個畫素 如果第i行j列元素G(i,j) >= a,則dhash += "1" 如果第i行j列元素G(i,j) <a, 則dhash += "0" |
得到圖片的phash值後,比較兩張圖片phash值的漢明距離,通常認為漢明距離小於10的一組圖片為相似圖片。
3.2 具體例項
仍用Lena圖來說明.

圖7 轉為灰度9x8尺寸的Lena圖
通過計算可得灰度9x8Lenna圖資料矩陣為:
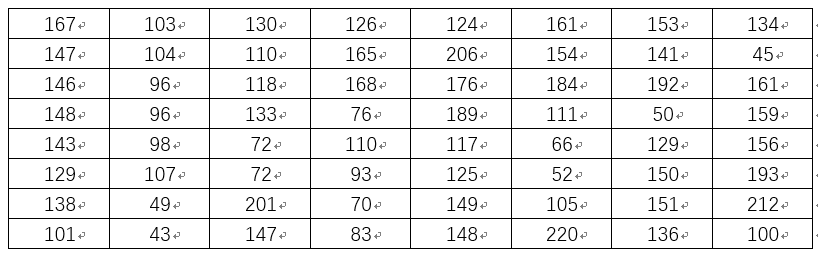
從第二行開始進行減去前一行操作,可得如下查分矩陣
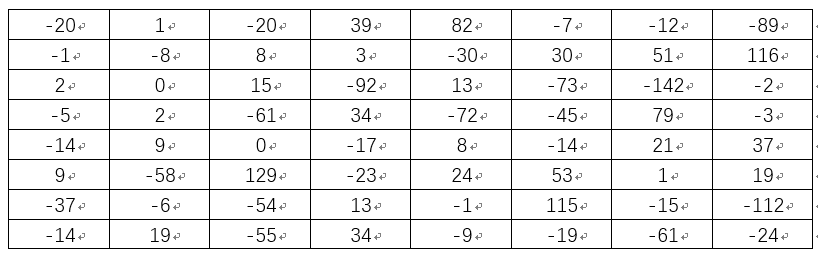
將上述矩陣中大於或等於0元素置為1, 小於a的元素置為0,可得:
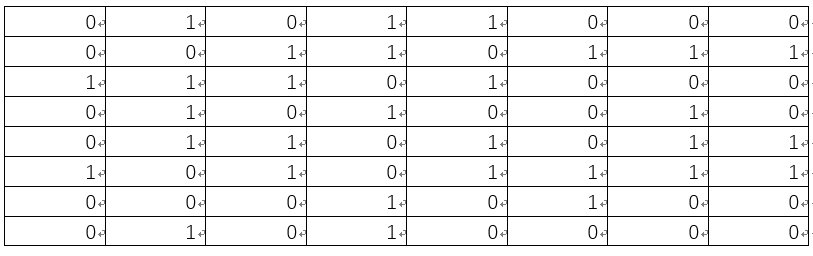
所以可得Lena圖的dHash為
0101100000110111111010000101001001101011101011110001010001010000
將二進位制形式dhash轉十六進位制hash為
99c4542560238280
為了測試dHash演算法的效果,同樣用一張帶噪聲Lena(noise)圖和與Lena不一樣的Barbara做圖片相似度對比實驗。通過pHash演算法容易得三個圖片的hash值,然後根據hanming距離計算Lena(origin).png和Lena(noise).png Barbar.png之間漢明距離,具體如下:

圖9 dHash演算法圖片相似度實驗
由上圖可見dHash能區別相似圖片和差異大的圖片。
總結
關於影象相似度演算法除了Hash演算法,在傳統演算法領域中還有基於SIFT的匹配演算法,基於Gist特徵的匹配演算法;在深度學習領域中有基於ResNet全連線的匹配演算法。感興趣的讀者可以通過google來了解這些演算法。
參考資料
432-Looks-Like-It
529-Kind-of-Like-That
本文程式碼
Github代
