100天搞定機器學習|Day 30-32 微積分的本質
3blue1brown系列課程,精美的動畫,配上生動的講解,非常適合幫助建立數學的形象思維,非常值得反覆觀看:
http://www.3blue1brown.com/

嗶哩嗶哩:
https://space.bilibili.com/88461692
作者還把製作視訊的用到的程式碼放到了 github 上,有興趣的同學可以研究看看
Github: https://github.com/3b1b/manim
我們節選其中一部分內容,領略一下微積分的奧妙
要了解微積分的本質,我們從一個大家都知道的公式說起。這個公式就是求圓的面積公式:A=πr²
我們將用微積分的方式來推導這個公式,在這個過程中,我們將利用到微分,積分,和兩者的互逆。
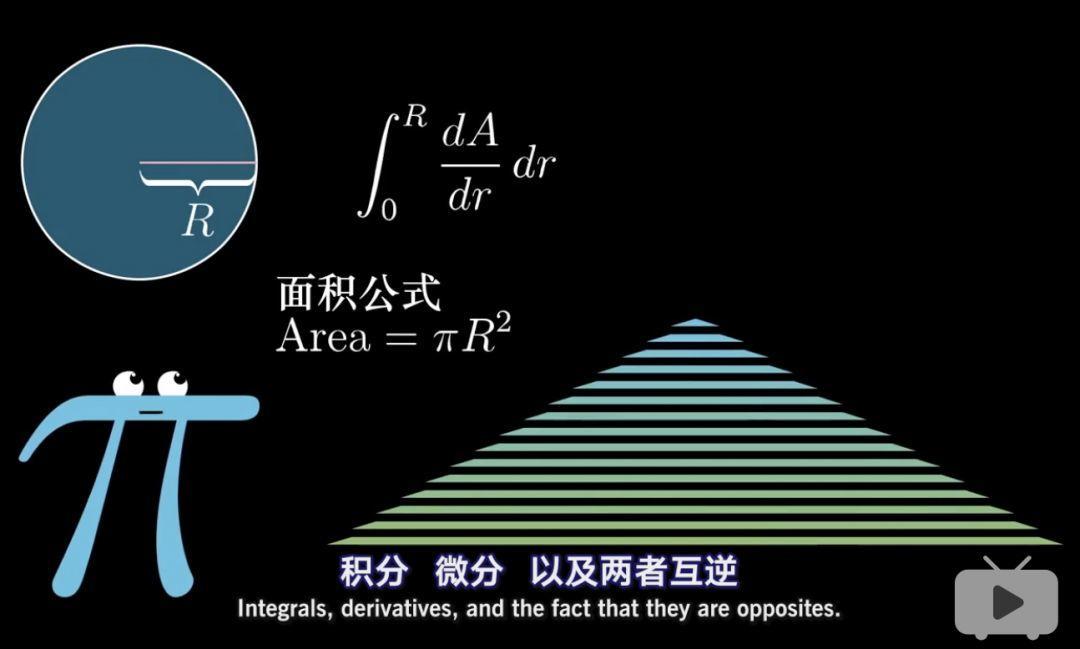
首先我們先將一個圓如下圖切分成數個圓環。我們獲得每個圓環的面積,然後將他們相加不就得到圓的面積了。
所以我們以相同的距離dr將圓切分成若干個同心圓環。
比如圓環的半徑是3,dr取0.1 那麼我們就將一個圓換分成了30個寬度都是0.1的同心圓環:

每一個圓環拉直會得到一個新的形狀,我們將這個形狀近似看做一個矩形
那麼這個矩形的面積就是這個圓環的周長乘以dr,圓環的周長為圓環到圓心的距離*2π
那麼每個圓環的近似面積面積就為:**2πr*dr**(這裡的r是每個圓環到圓心的距離)
你會發現我們的dr 取值越小,那麼我們計算出來的圓的面積也就越精確。

現在如果我們把所有近似矩從小到大一個接一個的排列在一起,我們會有一些全新的發現:
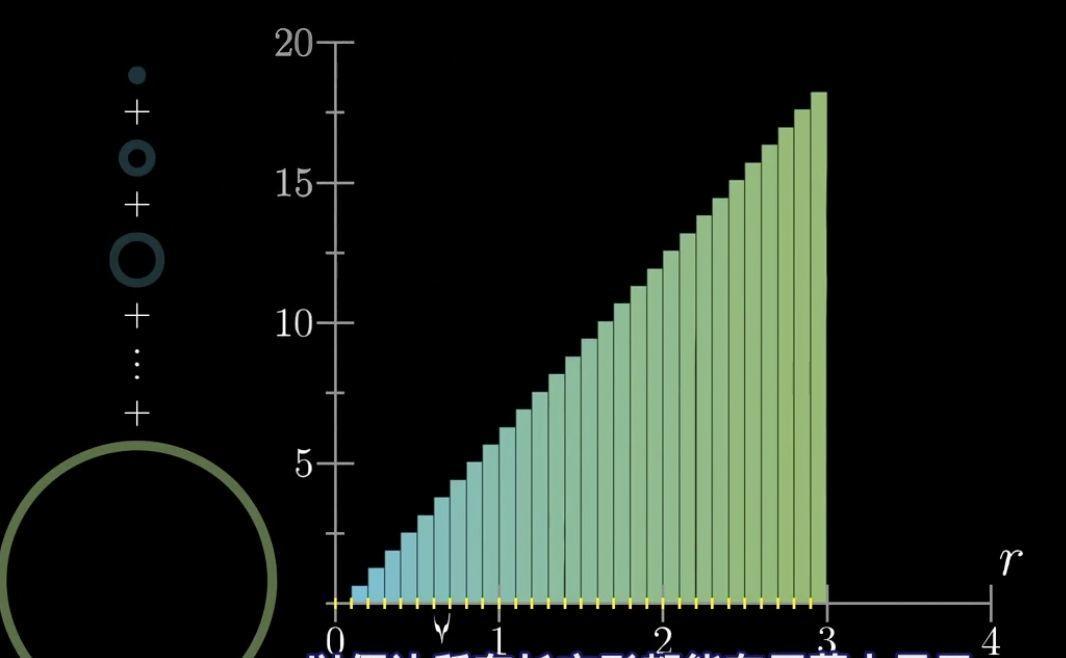
注意,為了方便觀察我們y軸與x軸的比例為5:1
現在我們去的dr是0.1,而我們取的dr值越小,獲得的圓環的數量就越多,而這些圓環的近似矩形面積相加起來的面積就靠近原來的圓的面積。
若是無限多個圓環,那麼我們獲得的近似值越來越靠近真實值。
可是我們取的圓環越多,那麼計算量不就越大,無限多的就代表根本沒法計算。
但注意,當dr取值無限小的時候,我們將所有圓環的面積加起來與下圖三角形的面積是相同的。
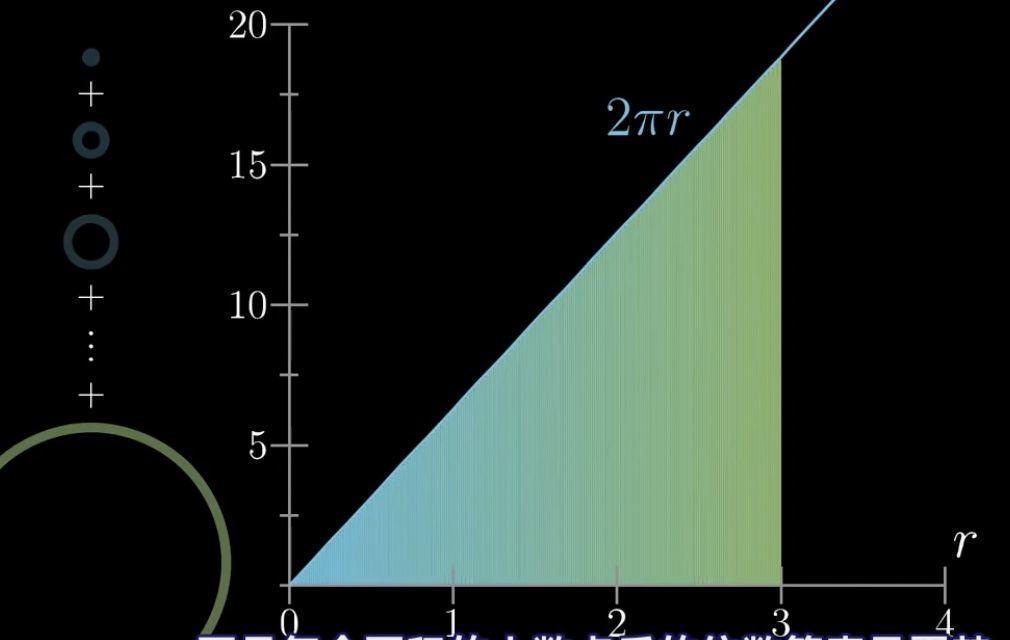
這個三角形的底是3 而高最大圓環的周長,也就是圓的周長:2π*3
如果圓的半徑是r,那麼它對應的三角形就是一個底為r,高為2π*r的三角形。根據三角形面積公式,我們得到
圓的面積為:πr²
對於數學家來說,你不光要找到答案,你還想要能發展處解決一般問題的工具和技巧
我們回想一下剛剛發生了什麼。為什麼這樣做是可行的。這個從近似值到精確值的過程,通過這個過程,我們可以瞭解微積分的本質。
最開我們將問題化解為許多微小值的和,來獲得一個近似的結果。
首先我們取每間隔dr值,取一個圓環。我們將一個圓換分成若干個小圓環,將其近似看成若干個矩形,我們就能獲得近似的圓形面積。
這裡的dr 不僅是圓環的寬度,也是每個圓環半徑的間距。
我們將這個這個dr越縮小,dr值取的越小,所有矩形相加的面積就越接近於一個三角形的面積。
我們可以得出結論,原來的原型的面積恰好就是這個三角形的面積。
注意此時已經不是近似值,而是完全準確。
通過這種方法,我們重新推導了計算圓的面積的公式。
現在我們看看這種方法在其他的地方如何發揮作用。
例如,已知騎車在每個時間點上的速度,求這段時間騎車走了多遠的距離。
我們可以用每個時間點的速度乘以這段微小的時間,然後相加求和,就是這一整段時間走的距離的近似值。
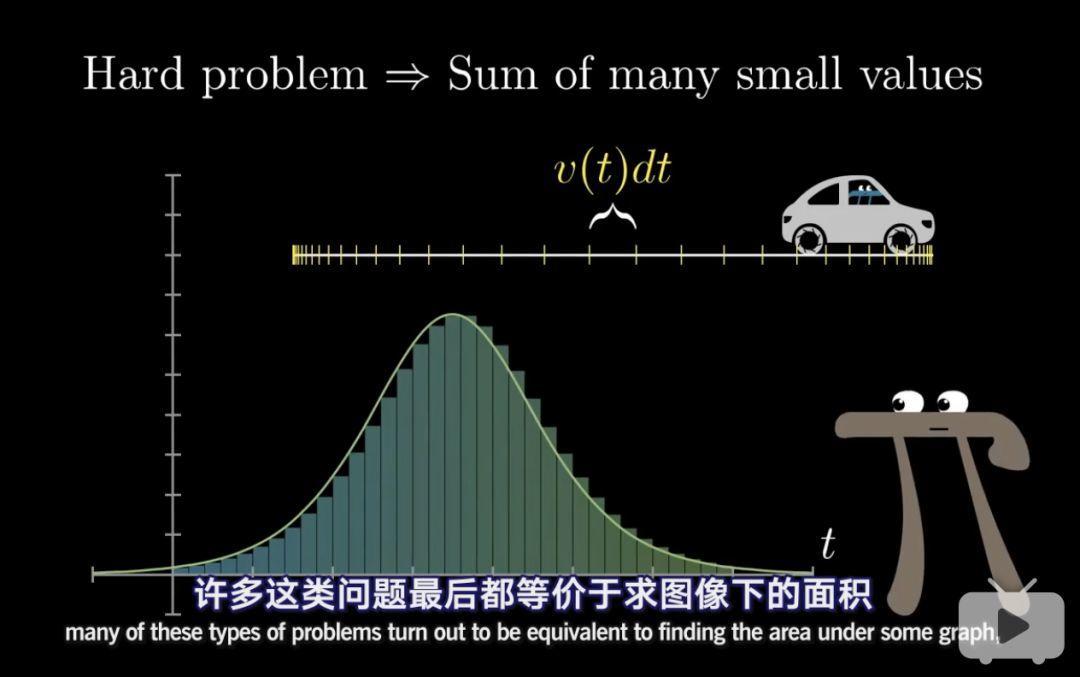
從圖中,我們可以看出,最後我們將一個物理學的問題,變成了幾何學的問題。這是不是很有趣?
還有很多的問題都可以這樣來計算,我們將一個複雜的問題,拆解為若干近似於a*b然後相加求和的問題(如上面的速度乘以時間),
其中每一個乘法計算中的a都是相同的。(如上一例子中,每一個時間點之間的距離是相同的,也就是vt中的t是相同的)
那麼我們就可以將問題轉化為若干細長的矩形面積(a*b不就是求矩形面積的公式?)相加取得近似值的問題。
若是我們取的a(在這個汽車例子中的t)取值越小,我們最終獲得的值就越精確,而且越發靠近求下圖面積的問題的。
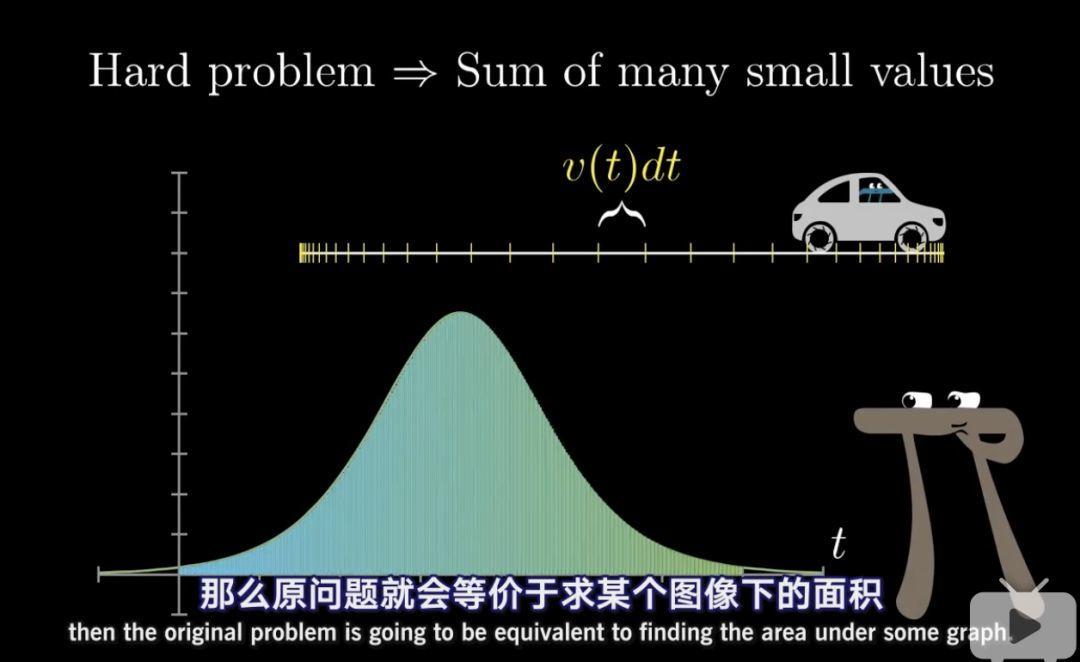
等等,這個形狀的面積似乎也不是那麼好求得。
似乎我們不會像求圓的面積的時候那麼的幸運,得到圖形正好是一個三角形。
如上題我們求一個汽車從發動到停止這段時間經過的距離,最後我們得到的這樣一個形狀,我們要怎麼求它的面積呢?
一個二次函式的曲線下的面積要怎麼求呢?
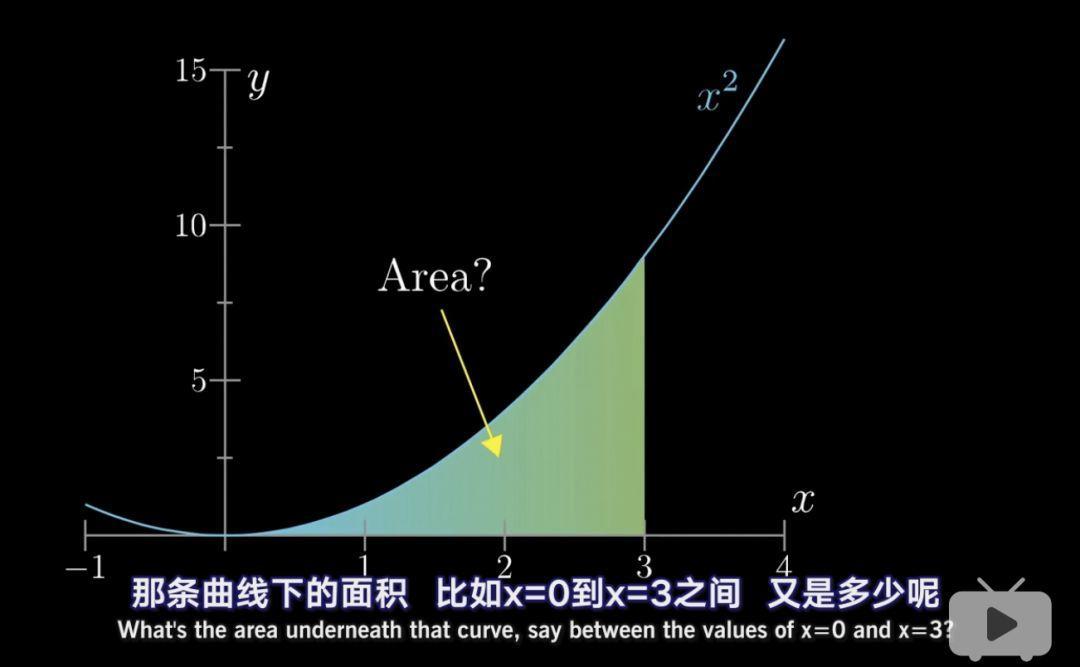
視訊告訴我們,當你在數學上遇到一個特別難解的問題是,不要想著正面硬解,這樣你往往會撞上南牆。
相反,你應該帶著不明確的目的不斷把玩這些概念。

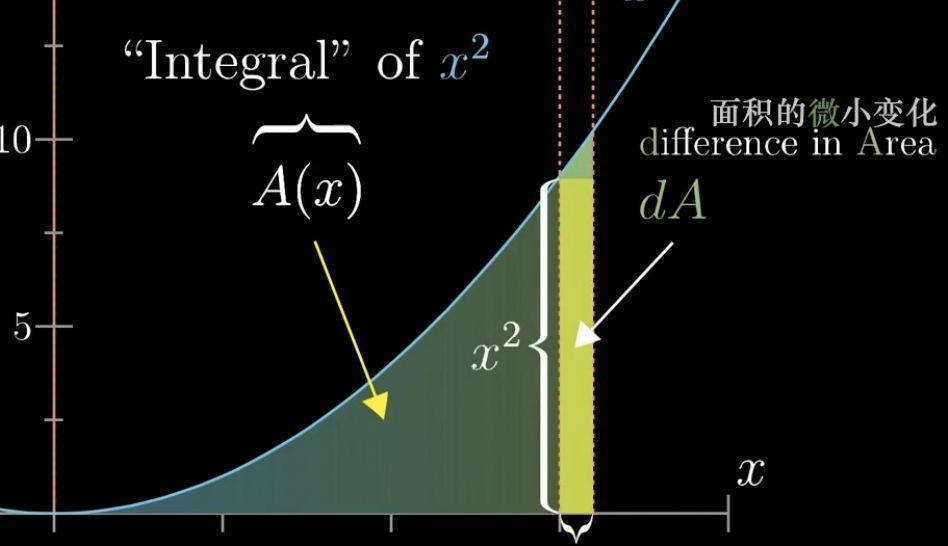
我們將二次函式,x²函式曲線下的面積設定A(x)
那麼A(x)與x²之間有什麼特殊關係呢?
如果我們將x的值增加一點點,那A(x²)的值回發生怎樣的變化呢?
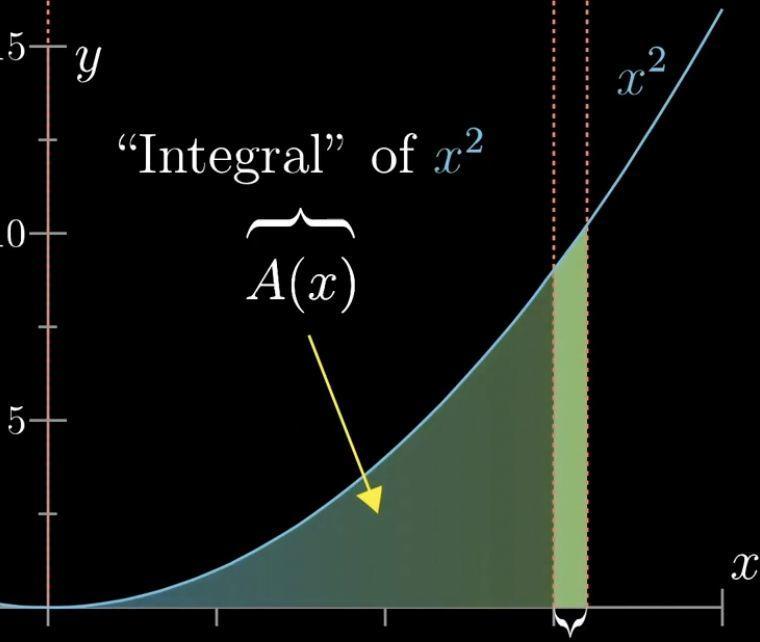
我們把增加的面積叫做dA,x的增加值叫做dx
我們將這個增加的面積近似看做一個矩形。
我們可以得到:
dA≈x²*dx 由此我們得到: dA/dx≈x²
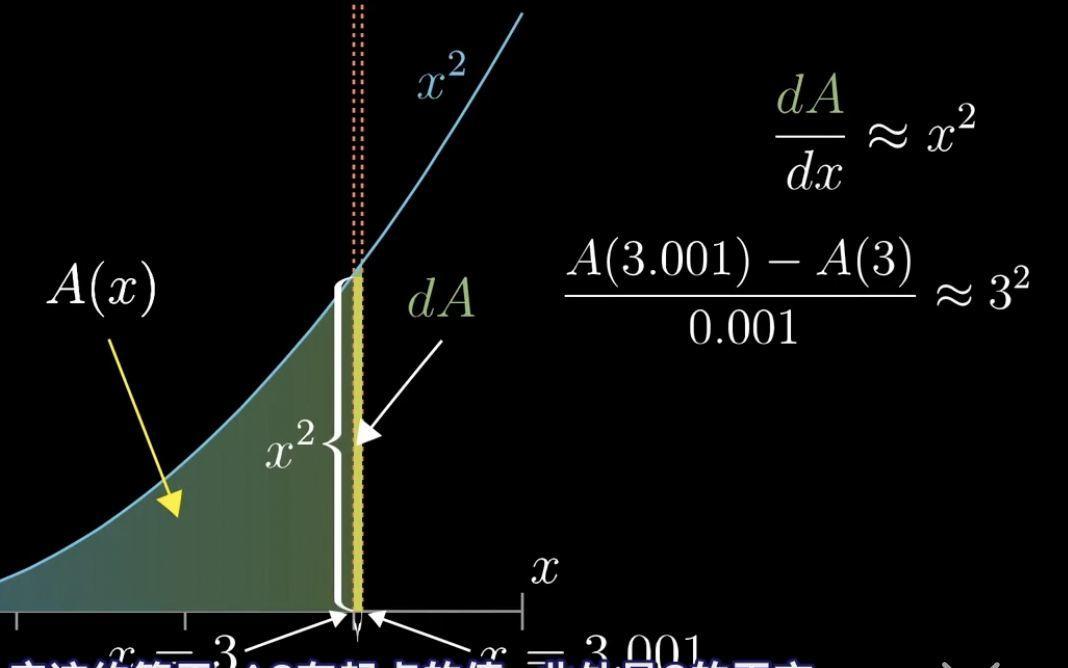
這裡我們dx的值取的越小,那麼這個dA的面積就越接近矩形的面積。dA/dx也就越接近x²
我們將x=3,dx0.001代入這個公式可以得到
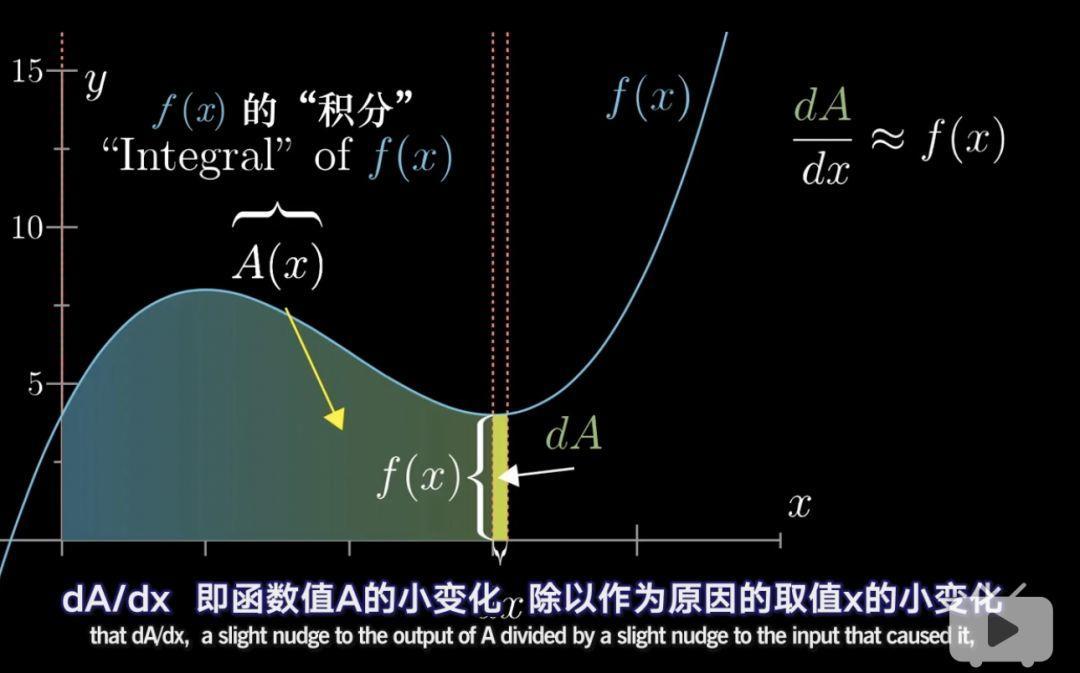
現在我們還是不知道神祕的A(x),但是我們有了這樣一個一個公式:dA/dx≈f(x)
dx取值越小,這個公式就越精確。
作者:guolaomao@cnblogs
https://www.cnblogs.com/guolaomao/category/1136473.h
