本文為3Blue1Brown神經網路課程講解第二部分《Gradient descent, how neural networks learn 》的學習筆記，觀看地址：www.bilibili.com/video/av16144388前文我們已經搭建了一個包含兩個隱藏層的神經網路，我們需要這樣一種演算法：網路得到訓練資料後，演算法會調整所有的權重和偏置值，提高網路對訓練資料的表現。我們還希望這種分層結構可以舉一反三，識別其他影象。訓練好網路後，再給它未見過的帶標記的資料作為測試，這樣就能知道新影象分類的準確度。

這實際上就是找某個函式的最小值，在一開始，我們會完全隨機地初始化所有的權重和偏置值。可想而知，這個網路對於給定的訓練示例，會表現得非常糟糕。例如輸入一個3的影象，理想狀態應該是輸出層3這個點最亮。可是實際情況並不是這樣。這是就需定義一個代價函式。

網路可以對影象正確分類時，這個平方和就比較小，反之就很大。接下來就要考慮幾萬個訓練樣本中代價的平均值。

神經網路本身是個函式，它有784個輸入值，10個輸出，13000多個引數。

代價函式則要再抽象一層，13000多個權重和偏置值作為他的輸入，輸出是單個數值，表示引數的表現優劣程度。

代價函式取決於網路對上萬個訓練資料的綜合表現，但是我們還需要告訴網路該如何改變這些權重和偏置值，讓其表現更好。為了簡化問題，我們先不去想一個有13000多個變數的函式，而考慮簡單的一元函式，只有一個輸入變數，只輸出一個數字。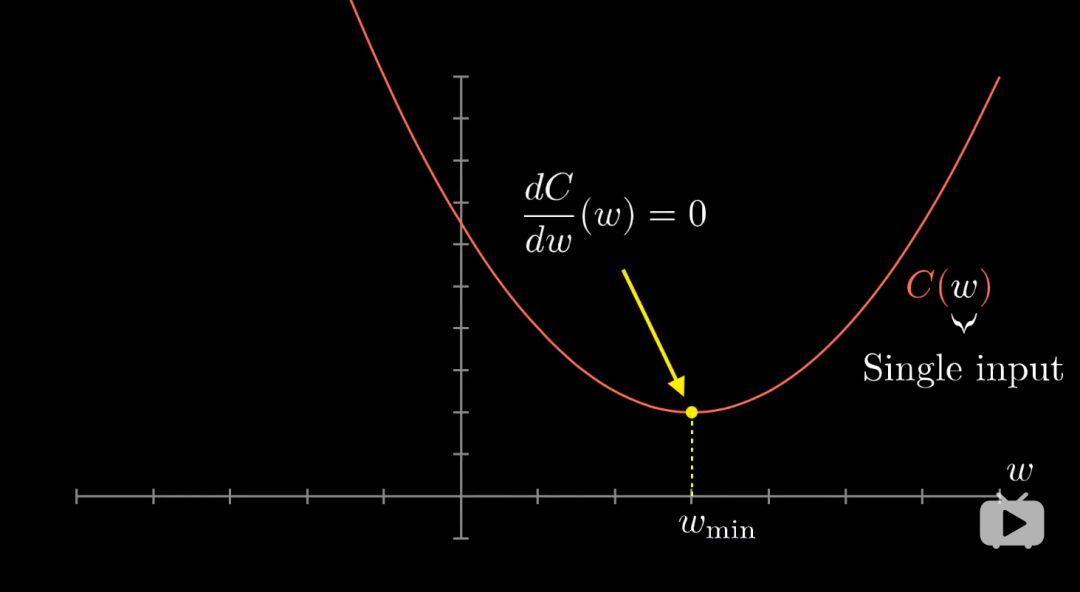

學過微積分的都知道，有時你可以直接算出這個最小值，不過函式很複雜的話就不一定能寫出，而我們這個超複雜的13000元的代價函式，就更加不可能做到了。一個靈活的技巧是：以下圖為例，先隨便挑一個輸入值，找到函式在這裡的斜率，斜率為正就向左走，斜率為負就向右走，你就會逼近函式的某個區域性最小值。（其實是沿著負梯度方向，函式減少的最快）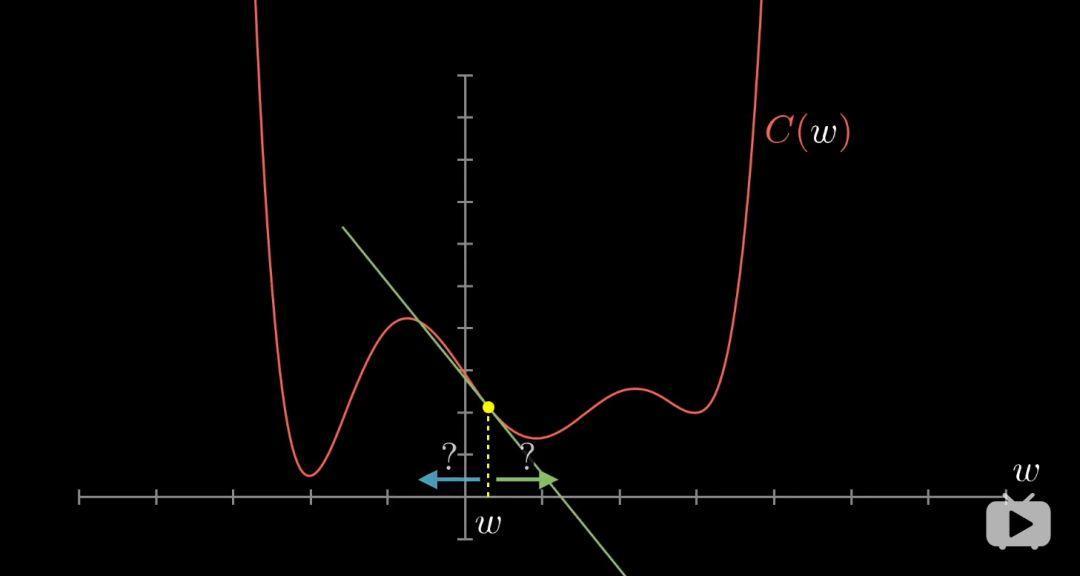

但由於不知道一開始輸入值在哪裡，最後你可能會落到許多不同的坑裡，而且無法保證你落到的區域性最小值就是代價函式的全域性最小值。值得一提的是，如果每步的步長與斜率成比例，那麼在最小值附近斜率會越來越平緩，每步會越來越小，這樣可以防止調過頭。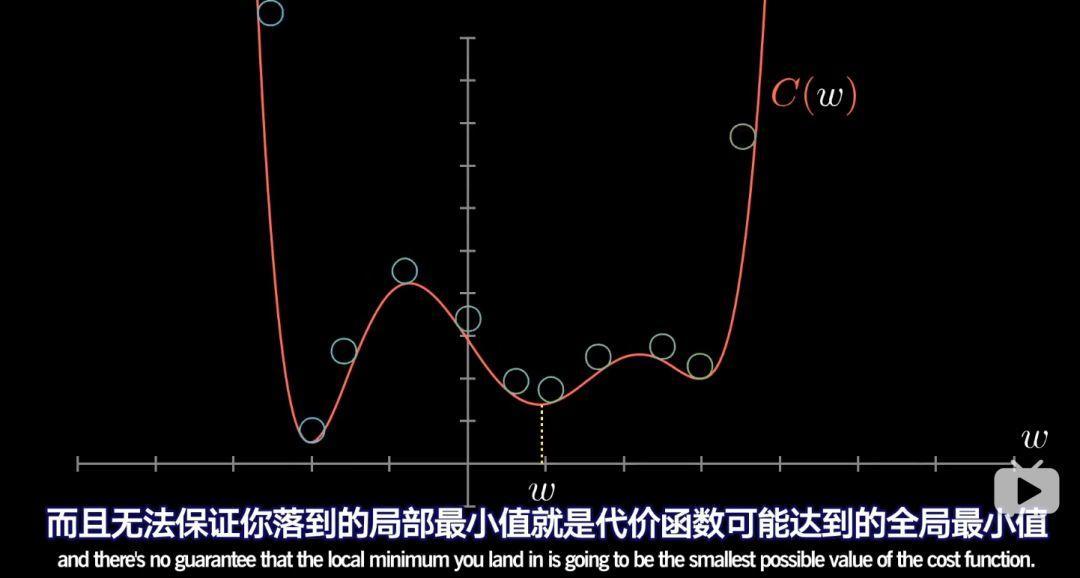

我們想象一個更復雜的兩個輸入一個輸出的二元函式，代價函式是圖中右側的紅色曲面。在輸入空間被沿著哪個方向走，才能使輸出結果下降最快？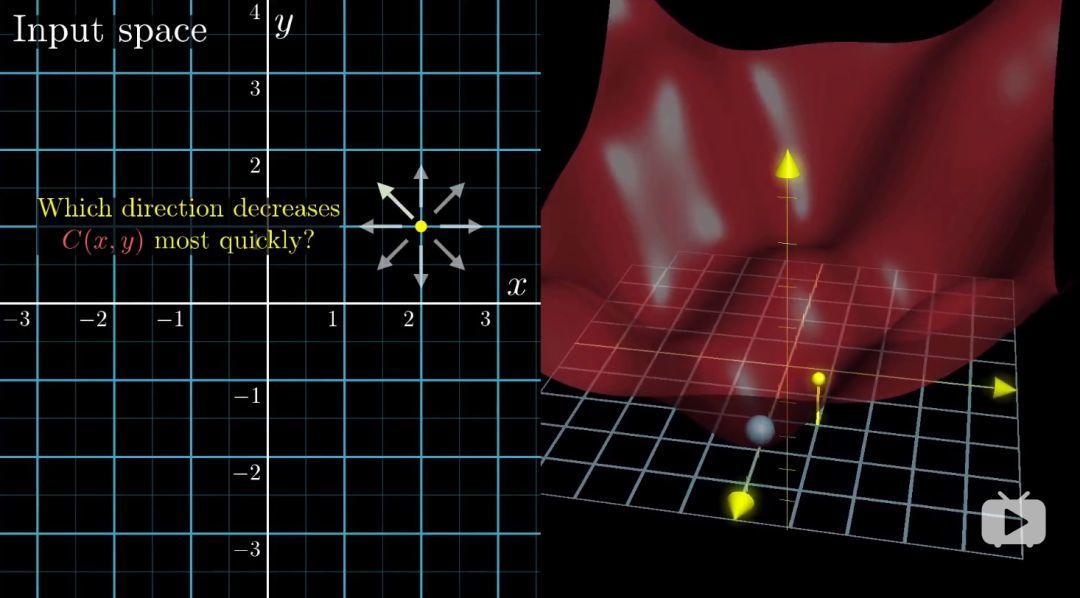

在多元微積分領域，函式梯度指的是函式的最陡增長方向，沿著其相反的方向，函式值下降的最快，梯度向量的長度代表了最陡的斜坡的到底有多陡峭。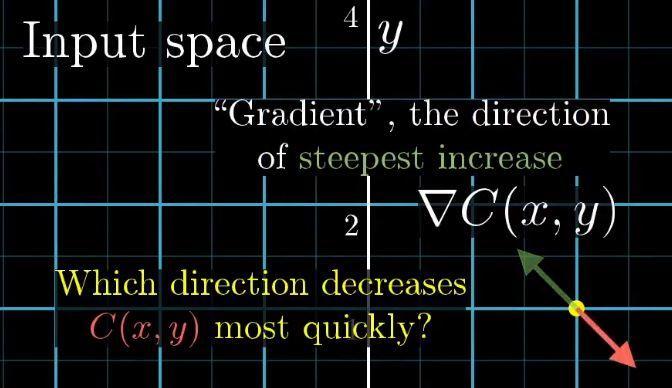

讓函式值最小的演算法其實就是先計算梯度，在按反方向走一小步，然後迴圈。處理13000個輸入的函式也是這個道理。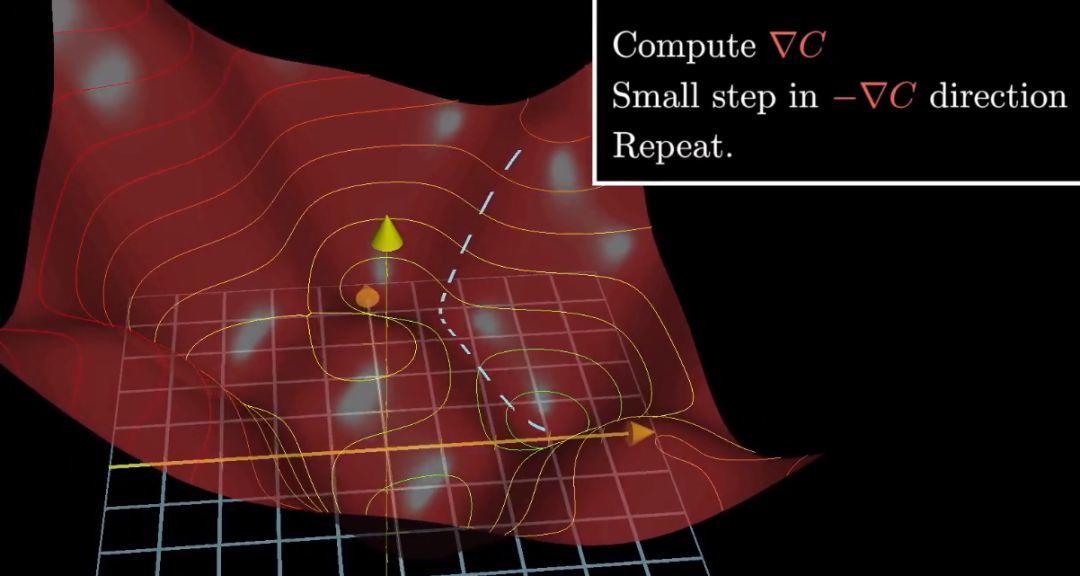

只是把這些權重、偏置都放在一個列向量中，代價函式的負梯度也是一個向量。負梯度指出了在這個函式輸入空間內，具體如何改變每一項引數，才能讓讓代價函式的值下降的最快。

對於這個我們設計的神經網路的代價函式，更新權重和偏置來降低代價函式的值，意味著輸入訓練集的每一份樣本的輸出，都會越來越接近真實結果。又因為我們選擇的是所有訓練樣本代價函式的平均值，所以最小化即對所有樣本得到的總體結果會更好。

當我們提到讓網路學習，實質上就是讓代價函式的值最小。代價函式有必要是平滑的，這樣我們才可以挪動以找到全域性最小值，這也就是為什麼人工神經元的啟用值是連續的。到這裡，我們終於引出了梯度下降法的定義：

負梯度內每一項值的正負號告訴我們輸入向量對應該調大還是調小，每一項的相對大小也告訴了我們哪個值影響更大，改變哪個引數值，價效比最高。

訓練後的神經網路就可以進行數字識別了，但是當輸入是一個噪音圖片時，神經網路卻仍很自信的把它識別成一個數字。換句話說，即使網路學會了如何識別數字，但是它卻不會自己寫數字。原因就在於網路的訓練被限制在很窄的框架內，對於第一層網路，它的視角整個宇宙都是由小網格內清晰定義的靜止數字組成的，它的代價函式則會促使它對最後的判斷有絕對的自信。研究越深，你就會發現，神經網路沒有那麼智慧。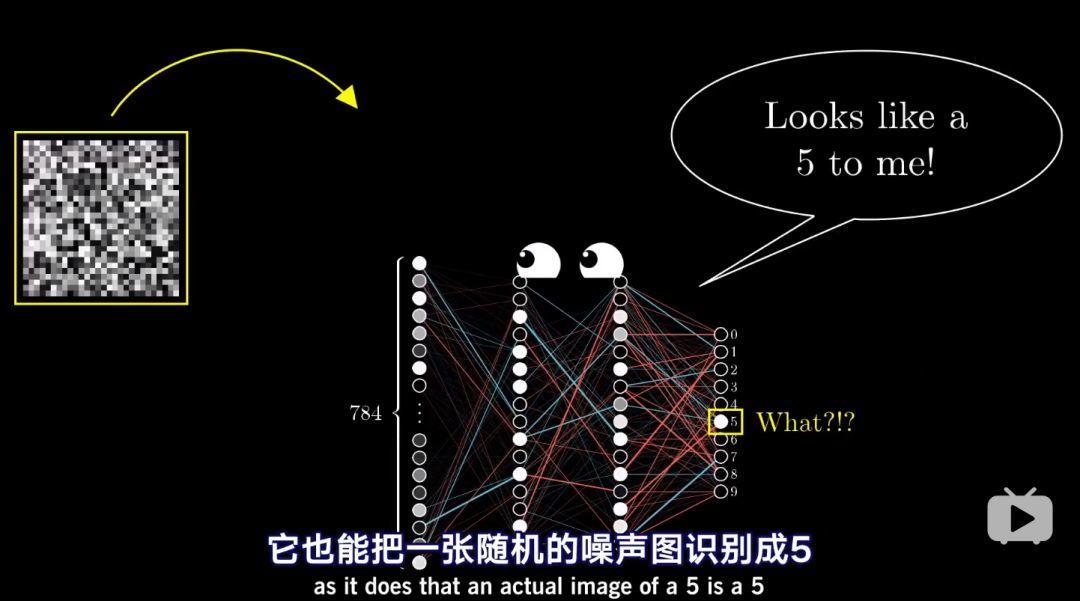

本節完！下節課我們學習3Blue1Brown關於神經網路的第3部分《偏導數和反向傳播法》