解開Batch Normalization的神祕面紗
停更部落格好長一段時間了,其實並不是沒寫了,而是轉而做筆記了,但是發現做筆記其實印象無法更深刻,因此決定繼續以寫部落格來記錄或者複習鞏固所學的知識,與此同時跟大家分享下自己對深度學習或者機器學習相關的知識點,當然淺薄之見如有說錯表達錯誤的,歡迎大家指出來。廢話不多說,進入今天的主題:Batch Normalization。
Batch Normalization(BN)是由Sergey Ioffe和Christian Szegedy在2015年的時候提出的,後者同時是Inception的提出者(深度學習領域的大牛),截止至動手寫這篇部落格的時候Batch Normalization的論文被引用了12304次,這也足以說明BN被使用地有多廣泛。在正式介紹BN之前,有必要了解下feature scaling(特徵歸一化),這是不論做傳統機器學習也好或者現在深度學習也好,預處理階段可以說是必不可少的一步也是確保模型能夠正常學習非常重要的一步。
1、為什麼需要使用feature scaling?
Feature scaling指的是對輸入的資料特徵進行歸一化操作(一般有min-max normalization或者min-max standardization兩種)以確保所有特徵的值處於同一維度。假設現在有x1和x2是兩個特徵,從公式a = Sigmoid(WTX + b)計算loss可以知道,如果x1和x2的特徵值差別很大的話但是假設他們對結果的影響力一致的話(如下圖所示),那麼意味著w1的數值維度會比較大, w2的數值維度則會比較小,而如果要使w1和w2有一個同等的變化(如果這樣子需要設定不同的learning rate進行更新,針對w2
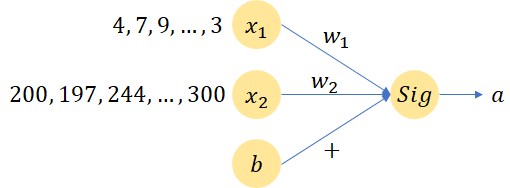
圖1 簡單的神經元計算流程
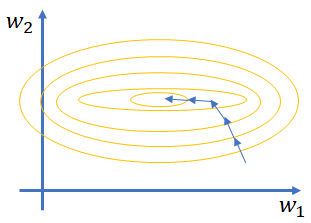
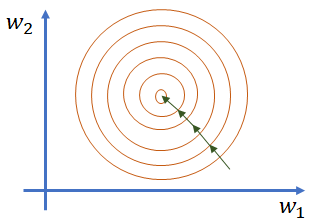
圖2 特徵值差異較大時的訓練過程(左)和特徵值大小處於同一維度的訓練過程(右)
一般的feature scaling是如何做呢?計算每個dimension的mean和每個dimension的std(feature scaling之後的每一維的值的均值為0,方差為1),做feature scaling之後梯度下降收斂會快點。當對輸入的特徵做完feature scaling之後,不免會引起一定困惑,那就是在神經網路中由於網路結構含有多層隱藏層,每一層隱藏層的輸入時下一層的輸入,那麼這些隱藏層的輸入(下面統一用這種說辭,避免混淆)是否需要也進行feature scaling呢?經過Sergey Ioffe和Christian Szegedy的驗證答案是肯定的。
2、神經網路中隱藏層為什麼要做feature scaling?
2.1 Internal Covariate Shift
在正式進入正題之前,同樣十分有必要解釋下Internal Covariate shift(ICS)是什麼以及對深度學習訓練模型的影響?在此之前,又得再先確認一個概念,那就是:深度學習和機器學習在進行模型訓練的時候都是基於資料IID(Independently identically distribution,獨立同分布)的情況。那什麼是獨立同分布呢?獨立(兩個事件沒有關聯)意味著資料之間(一般指訓練資料和測試資料,測試資料一般又指未見過的資料)是相互獨立的,同分布則指明資料具有相同分佈形狀並且具有相同分佈的引數(這裡可以想象下為為什麼針對取樣自統一分佈的資料進行模型訓練和學習,例如想象下引數的變化,資料集拆分符合分佈規律等等,也就能明白IID是如何影響深度學習模型和機器學習模型的),更直觀點說就是選取用於訓練的資料要具有全域性代表性,以便可以對未知的資料進行預測。
那什麼又是ICS呢?在神經網路的設計往往都是含有多個隱藏層,而像之前說的當前隱藏層的輸出是下一個隱藏層的輸入,把這個輸入當作一個分佈來看的話,而由於為了使訓練收斂引數不斷處於更新之中,當前隱藏層的引數更新之後會影響下一個隱藏層的輸入,也就是說由於引數的改變,輸入改變了(也就是分佈改變了),這個跟基於IID的假設是相違背的,出現這種現象則稱之為ICS(可通過設定小一點的學習率可以改善,但是小的學習率影響訓練速度因為步長變短了)。
2.2 Batch Normalization
為了降低ICS所帶來的影響,BN就被提出來了。這裡我們來看下通常神經網路結構是如何設計的: x with feature scaling -> layer1 -> a1(feature scaling?) -> layer2 -> a2(feature scaling?) 。那既然是叫Batch Normalization,那麼就意味著這個normalization是針對一個Batch一個batch的。這裡再複習下Batch訓練的一些基本原理,batch的意思是訓練網路的時候一次性拿幾個樣本並行的做計算,比如batch=4,那麼就是四個樣本作為輸入一起乘上同一個引數(如下圖3所示)。
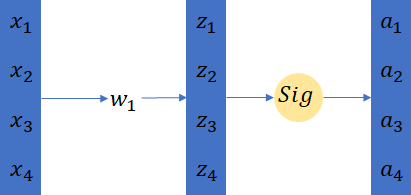
圖3 Batch Training
實際運算中,batch=4的四個樣本會被拼成一整個matrix,這裡從程式設計的角度想想會更好理解,例如要對1萬張圖片進行訓練,選取batch=4,假設每個圖片的高和寬為224和224,通道數為3,那麼他們的shape就是(4,224,224,3),這個用numpy或者PyTorch或者TensorFlow來在電腦上展示出來都是一個矩陣。Batch normalization是如何作用在batch上的呢?一般是先BN後activation,如果先做activation再做BN的話,input就有可能落在saturation值域上(tanh和sigmoid都容易存在這個問題),那麼就會產生gradient vanishing(梯度消失)的問題。接下來看看Batch Normalization的計算,一般是基於batch計算μ和σ的(均值和標準差),由於整個資料集量很大,如果是針對整個資料集計算μ和σ的話,那麼計算開銷很大,所以BN是作用在batch上的資料,這也由此引申出一個問題,那就是在使用BN的時候,batch應該儘量設定比較大(batch < n where n is the number of samples),BN的計算演示圖如下圖所示:

圖4 引入BN的神經網路結構圖
那麼使用BN的話怎麼進行訓練呢?使用BN的時候,在做BP的時候也同樣需要去更新計算出來的batch的μ和σ,因為μ和σ也會影像training loss。在經過BN之後,資料的值的分佈是服從mean為0,方差為1的。但是有時候並不是服從這樣子的分佈才是網路更robust,所以此時希望對做了BN之後的數值做一個scale和偏移。這也就是論文中的β和γ存在的因素。但是仔細的人應該可以看出來,最後一個公式是計算μ和σ的來normalize輸入的逆過程,如果當μ、σ(calculated from batch)和γ、β一樣的話,就等於BN沒有任何作用。但是此時需要注意的是,μ和σ是受到每一層的輸入的影響的,但是γ和β是獨立的,不受輸入的影響,並且γ和β是整個網路的引數。通過上面的講述,可以清楚看到BN在訓練神經網路模型的過程中引入了四個新的需要被訓練的引數:μ、σ、γ和β。下圖是來自論文的上述引數的每個計算公示:

圖5 原論文中的計算公式
使用BN在測試階段同樣會遇到一個問題,因為我們知道在training的時候是一個Batch一個Batch進行訓練的,但是測試的時候(做預測時)是沒有所謂的batch之說的。這個時候一個比較實用的操作就是計算在訓練過程μ和σ的moving average,並且讓在靠近訓練結束的位置佔比較大的權重,而剛開始訓練的時候佔比較小的權重。
最後,來看看使用BN所帶來的好處都有哪些:
- 減少訓練時間,這是因為ICS所帶來的的影響減小了,由此可以使用較大的學習率;
- 避免梯度爆炸或者梯度消失(尤其在使用sigmoid和tanh這類啟用函式的時候);
- 學習率受引數初始化的影響減小;
- 讓訓練的模型不那麼容易過擬合(overfitting);
- 減少對正則化的依賴(如減少使用dropout);
