opencv之霍夫曼變換
霍夫變換不僅可以找出圖片中的直線,也可以找出圓,橢圓,三角形等等,只要你能定義出直線方程,圓形的方程等等.
不得不說,現在網上的各種部落格質量真的不行,網上一堆文章,亂TM瞎寫,誤人子弟.本身自己就沒有理解的很清楚,又不去讀演算法實現的原始碼,寫的雲山霧罩的,越看越懵逼.
霍夫變換本身的思路是很簡明的.這篇文章我們就以霍夫直線變換說明演算法的思想.
霍夫變換
思考一下,二維平面裡我們怎麼表達直線.
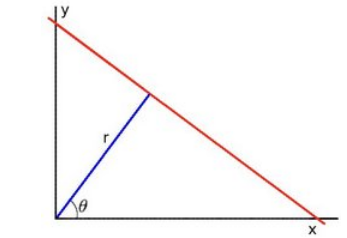
有兩種表達方式:
- 直角座標系(也叫笛卡爾座標系)
- 極座標系(也叫球座標系)
第一種就是最常見的直角座標系下的表達:y=ax+b的形式.
第二種就是極座標系下的表達:
我們把直角座標系下的直線方程用r,theta去表達直線方程的斜率和截距.
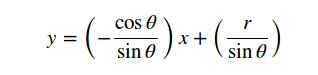
則得到極座標下的表達: r=xcosθ+ysinθ
假設影象中某畫素點座標為(x,y).在直角座標系下穿過這一點我們可以畫出無數條直線.
轉化到一個r-θ座標系下,我們就可以繪製出一條曲線.也就是r=xcosθ+ysinθ中的x,y是已知數,θ和r是未知數
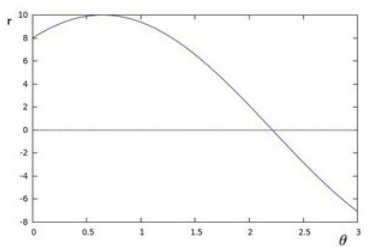
這條曲線上每一個θ對應一個r,代表了一條直線.這些直線的共同點是他們都穿過了座標為(x,y)的畫素點.

針對影象中的每一個畫素點,我都可以繪製出一條曲線來表達穿過該點的無數條直線. 那曲線的交點代表什麼呢? 很顯然,代表著交點處的(θ,r)所代表的直線即穿過了畫素點A,又穿過了畫素點B,畫素點C....
怎麼樣叫做"找到圖中的一條直線"
回到我們的問題,我們想找出影象中的一條線.意味著什麼?
很多部落格說了,意味著找出一條直線,儘可能多地穿過各個畫素點.

我TM隨便在影象上畫直線,不都能穿過很多畫素點嗎?
實際上,應該是找出一條直線儘可能多地穿過"有效畫素點".這也是為什麼霍夫變換前一定要先做邊緣檢測的原因.經過canny檢測以後(不知道的參考上一篇文章),得到的影象矩陣,只有在邊緣處其畫素灰度值才是比較大的,反映在影象上就是白色亮點,在非邊緣處,其灰度值是0,反映在影象上就是黑色.這些代表了邊緣的畫素點就是有效畫素點.
即:假如我能找到這麼一條直線,穿過了很多個有效畫素點(這個就是我們需要調參的閾值),那我就說我在影象中找到了一條直線. . 同理,找圓,找三角形還是找任意形狀都是一個道理.
比方說,下面這個圖

你就找不到一條直線,穿過很多個白點.所以圖中是不存在直線的.
霍夫變換的過程
- canny邊緣檢測提取出邊緣
- 對邊緣影象中的每個畫素點,
虛擬碼如下
for (every pixel)
{
if(pixel is effective edge pixel)
{
for(int theta = 0; theta < 360; theta++)
{
r=xcosθ+ysinθ;//x,y為pixel座標
accum(theta,r) += 1; //(theta,r)所代表的直線經過的畫素點數量加1
}
}
}
for(every element in accum)
{
if (count of (theta,r) > thershold)
{
find line (theta,r)
}
}
opencv示例
houghlines api
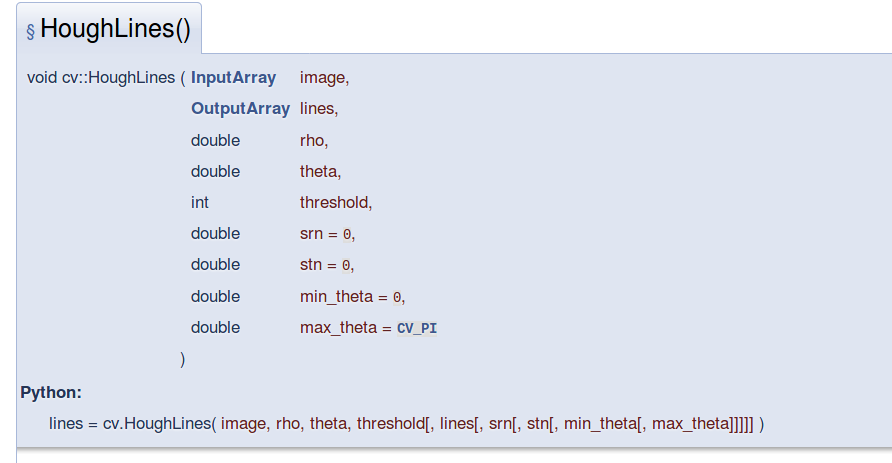

其中, double rho, double theta,決定了最終有多少種(theta,r)的組合.決定了過每個畫素點的線的可能情況.這個值越小,粒度就越細,需要的計算量也越大. 一般取rho=1,即1畫素.theta取1度.
下面是一個提取車點陣圖片中直線的示例
import sys
import math
import cv2 as cv
import numpy as np
def test():
src = cv.imread("/home/sc/disk/keepgoing/opencv_test/houghtest.jpg")
src = cv.GaussianBlur(src, (3, 3), 0)
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
dst = cv.Canny(src, 150, 300, None, 3)
lines = cv.HoughLines(dst, 1, np.pi / 180, 150, None, 0, 0)
# Copy edges to the images that will display the results in BGR
cdst = cv.cvtColor(dst, cv.COLOR_GRAY2BGR)
cdstP = np.copy(cdst)
lines = cv.HoughLines(dst, 1, np.pi / 180, 200, None, 0, 0)
if lines is not None:
for i in range(0, len(lines)):
rho = lines[i][0][0]
theta = lines[i][0][1]
a = math.cos(theta)
b = math.sin(theta)
x0 = a * rho
y0 = b * rho
pt1 = (int(x0 + 1000*(-b)), int(y0 + 1000*(a)))
pt2 = (int(x0 - 1000*(-b)), int(y0 - 1000*(a)))
cv.line(cdst, pt1, pt2, (0,0,255), 3, cv.LINE_AA)
cv.imshow("origin",src)
cv.imshow("dst1",dst)
cv.imshow("dst2",cdst)
if 27 == cv.waitKey():
cv.destroyAllWindows()
test()

opencv原始碼解讀
opencv 官方實現
static void
HoughLinesStandard( InputArray src, OutputArray lines, int type,
float rho, float theta,
int threshold, int linesMax,
double min_theta, double max_theta )
{
CV_CheckType(type, type == CV_32FC2 || type == CV_32FC3, "Internal error");
Mat img = src.getMat();
int i, j;
float irho = 1 / rho;
CV_Assert( img.type() == CV_8UC1 );
CV_Assert( linesMax > 0 );
const uchar* image = img.ptr();
int step = (int)img.step;
int width = img.cols;
int height = img.rows;
int max_rho = width + height;
int min_rho = -max_rho;
CV_CheckGE(max_theta, min_theta, "max_theta must be greater than min_theta");
int numangle = cvRound((max_theta - min_theta) / theta);
int numrho = cvRound(((max_rho - min_rho) + 1) / rho);
#if defined HAVE_IPP && IPP_VERSION_X100 >= 810 && !IPP_DISABLE_HOUGH
if (type == CV_32FC2 && CV_IPP_CHECK_COND)
{
IppiSize srcSize = { width, height };
IppPointPolar delta = { rho, theta };
IppPointPolar dstRoi[2] = {{(Ipp32f) min_rho, (Ipp32f) min_theta},{(Ipp32f) max_rho, (Ipp32f) max_theta}};
int bufferSize;
int nz = countNonZero(img);
int ipp_linesMax = std::min(linesMax, nz*numangle/threshold);
int linesCount = 0;
std::vector<Vec2f> _lines(ipp_linesMax);
IppStatus ok = ippiHoughLineGetSize_8u_C1R(srcSize, delta, ipp_linesMax, &bufferSize);
Ipp8u* buffer = ippsMalloc_8u_L(bufferSize);
if (ok >= 0) {ok = CV_INSTRUMENT_FUN_IPP(ippiHoughLine_Region_8u32f_C1R, image, step, srcSize, (IppPointPolar*) &_lines[0], dstRoi, ipp_linesMax, &linesCount, delta, threshold, buffer);};
ippsFree(buffer);
if (ok >= 0)
{
lines.create(linesCount, 1, CV_32FC2);
Mat(linesCount, 1, CV_32FC2, &_lines[0]).copyTo(lines);
CV_IMPL_ADD(CV_IMPL_IPP);
return;
}
setIppErrorStatus();
}
#endif
Mat _accum = Mat::zeros( (numangle+2), (numrho+2), CV_32SC1 );
std::vector<int> _sort_buf;
AutoBuffer<float> _tabSin(numangle);
AutoBuffer<float> _tabCos(numangle);
int *accum = _accum.ptr<int>();
float *tabSin = _tabSin.data(), *tabCos = _tabCos.data();
// create sin and cos table
createTrigTable( numangle, min_theta, theta,
irho, tabSin, tabCos);
// stage 1. fill accumulator
for( i = 0; i < height; i++ )
for( j = 0; j < width; j++ )
{
if( image[i * step + j] != 0 )
for(int n = 0; n < numangle; n++ )
{
int r = cvRound( j * tabCos[n] + i * tabSin[n] );
r += (numrho - 1) / 2;
accum[(n+1) * (numrho+2) + r+1]++;
}
}
// stage 2. find local maximums
findLocalMaximums( numrho, numangle, threshold, accum, _sort_buf );
// stage 3. sort the detected lines by accumulator value
std::sort(_sort_buf.begin(), _sort_buf.end(), hough_cmp_gt(accum));
// stage 4. store the first min(total,linesMax) lines to the output buffer
linesMax = std::min(linesMax, (int)_sort_buf.size());
double scale = 1./(numrho+2);
lines.create(linesMax, 1, type);
Mat _lines = lines.getMat();
for( i = 0; i < linesMax; i++ )
{
LinePolar line;
int idx = _sort_buf[i];
int n = cvFloor(idx*scale) - 1;
int r = idx - (n+1)*(numrho+2) - 1;
line.rho = (r - (numrho - 1)*0.5f) * rho;
line.angle = static_cast<float>(min_theta) + n * theta;
if (type == CV_32FC2)
{
_lines.at<Vec2f>(i) = Vec2f(line.rho, line.angle);
}
else
{
CV_DbgAssert(type == CV_32FC3);
_lines.at<Vec3f>(i) = Vec3f(line.rho, line.angle, (float)accum[idx]);
}
}
}stage1即核心邏輯,挨個遍歷有效畫素,統計出各種(theta,r)代表的直線穿過的畫素點點的數量
Mat _accum = Mat::zeros( (numangle+2), (numrho+2), CV_32SC1 );
可以看到統計直線穿過的點數量的矩陣的個數是 (2 + numangle) x (numrho+2),即與我們傳入的double rho, double theta有關.這個值越小,相應的我們搜尋的直線數量就越多.
opencv的實現裡有一些可能是出於工程上的考慮,這點不太確定,比如這裡為什麼要(2 + numangle) x (numrho+2) 而不是 numangle x numrho
int max_rho = width + height;
int min_rho = -max_rho;為什麼是w + h,而沒有用開平方根求對角線長度.
希望知道的朋友可以留言告訴我.
// stage 2. find local maximums
static void
findLocalMaximums( int numrho, int numangle, int threshold,
const int *accum, std::vector<int>& sort_buf )
{
for(int r = 0; r < numrho; r++ )
for(int n = 0; n < numangle; n++ )
{
int base = (n+1) * (numrho+2) + r+1;
if( accum[base] > threshold &&
accum[base] > accum[base - 1] && accum[base] >= accum[base + 1] &&
accum[base] > accum[base - numrho - 2] && accum[base] >= accum[base + numrho + 2] )
sort_buf.push_back(base);
}
}尋找計數的區域性最大值.類似於非極大值抑制.進一步細化檢測到的直線,把區域性的很相似的直線只取最精準的.
// stage 3. sort the detected lines by accumulator value
按accum數量大小排序
// stage 4. store the first min(total,linesMax) lines to the output buffer
儲存前n條lines到輸出Buff
