在影象分割邊緣檢測一文中介紹了一些有效的邊緣檢測方法，但在實際中由於噪聲和光照不均等因素，使得很多情況下獲得的邊緣點不連續，必須通過邊緣連線將它們轉換為有意義的邊緣。一般的做法是對經過邊緣檢測的影象進一步使用連線技術，從而將邊緣要素組合成完整的邊緣。霍夫變換就是實現著一功能的方法，它是一個非常重要的檢測間斷點邊界的方法。它通過將影象座標空間變換到引數空間，來實現直線和曲線的擬合。
1， 直線檢測
在座標空間中，經過一點p的直線可以有無數條，對應於不同的斜率（a）和截距(b)。如果將p點的座標視為常數，而將原本得到的引數a與b視為變數，便可變換到引數平面a-b。這個變換就是直角座標對於p的Hough變換。該直線是影象座標空間中的點p在引數空間的唯一方程。考慮影象座標空間中另一點q，它在引數空間中也有相應的一條直線，p與q在引數空間的直線交於一點o，這一點o就是影象座標空間中p和q所確定的直線的引數。也就是說，在引數空間相交於同一點的所有直線，在影象空間都有共線的點與之對應。根據這個特性，給定影象座標空間的一些邊緣點，就可以通過Hough變換確定連線這些點的直線方程。具體計算時，可以把引數空間視為離散。建立一個二維累加陣列A(a,b)，第一維的範圍是影象座標空間中直線斜率的可能範圍，第二維的範圍是影象座標空間中直線截距的可能範圍。這類陣列也被稱為Hough矩陣。與直角座標類似，極座標中的Hough變換也將影象座標空間中的點變換到引數空間中。在極座標下，影象座標空間中共線的點變換到引數空間之後，在引數空間都相交於同一點，此時得到的極座標即為所求直線的極座標引數。與直角座標不同的是，用極座標表示時，影象座標空間的共線兩點對映到引數空間是兩條正弦曲線。
2， 曲線檢測
Hough變換同樣適用於方程已經知道的曲線檢測。影象座標空間中的一點，在引數空間中也可以對映為相應的軌跡曲線或者曲面。若引數空間中對應各個間斷點的曲線或者曲面能夠相交，就能夠找到引數空間的極大值以及對應的引數，若引數空間中對應各個間斷點的曲線或者曲面不能相交，則說明這間斷點不符合某已知曲線，Hough變換做曲線檢測時，最重要的是寫出影象座標空間到引數空間的變換公式，曲線檢測也可以有極座標的形式。
3， 任意形狀的檢測
用Hough變換去檢測某一任意形狀邊界的圖形。首先需要選擇該圖形中的任意一點p為參考點，然後從該圖形的邊緣上每一點計算其切線方向和到參考點p位置偏移向量，以及該向量與x軸的夾角。具體的步驟為（1）在預知區域形狀的條件下，將物體邊緣形狀編成參考表。對於每個邊緣點計算梯度角，對每一個梯度角算出對應於參考點的距離和角度。（2）在引數空間建立一個二維累加陣列A，初值為0，對邊緣上的每一點，計算出該點處的梯度角，然後計算出每一個可能的參考點的位置值，對相應的陣列元素加一。(3)計算結束後，具有最大值的陣列元素A所對應的座標值即為影象座標中所求的參考點，求出參考點後，整個目標的邊界就可以確定了。
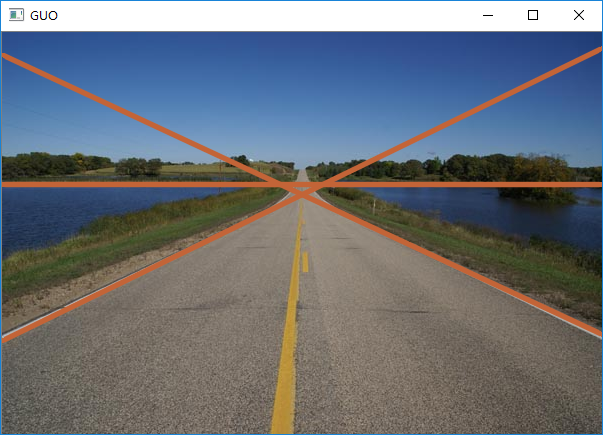
Hough變換直線檢測的openCV實現

void huoFu(){
    Mat srcImg = imread("hw.bmp");
//  imshow("SRC", srcImg);

    Mat midImg, dstImg;
    Canny(srcImg, midImg, 50,200,3);
    cvtColor(midImg, dstImg, CV_GRAY2BGR);
    //imshow("dst", dstImg);

    vector<Vec2f>lines;
    HoughLines(midImg, lines, 1, CV_PI / 180, 190, 0, 0);

    for (size_t i = 0
 
; i < lines.size(); ++i){
        //rho表示直線到原點的垂距離，theta代表x軸到直線垂直的角度
        float rho = lines[i][0], theta=lines[i][1];
        Point pt1, pt2;
        double a = cos(theta), b = sin(theta);//座標轉換對映到引數空間
        double x0 = a*rho, y0 = b*rho;
        //確定直線的起始點
        pt1.x = cvRound(x0 + 1000 * (-b));
        pt1.y = cvRound(y0 + 1000
 
 * (a));
        pt2.x = cvRound(x0 - 1000 * (-b));
        pt2.y = cvRound(y0 - 1000 * (a));
        //連線起始點
        line(srcImg, pt1, pt2, Scalar(55, 100, 195), 4, CV_AA);
    }
    imshow("GUO", srcImg);

    waitKey(0);
}