詞法分析

編譯原理筆記第三部分，內容參考：北航軟院教師邵兵課堂課件及內容、張莉著《編譯原理及編譯程式構造》、國防工業出版社的《編譯原理——學習指導與典型題解析》、AlvinZH的學習筆記以及個人理解

目前是包含了全部內容的版本，後續會推出精簡版和複習知識點版

如有建議或錯誤錯誤歡迎在評論中指出或聯絡我：QQ：847590417

總閱讀目錄

本章總內容

第一部分：

3.1 詞法分析程式的功能及實現方案

3.2 單詞的種類及詞法分析程式的輸出形式

3.3 正則文法及狀態圖

3.3.1 狀態圖

3.3.2 狀態圖的使用

3.4 正則表示式與有窮自動機FA

3.4.1 正則表示式

3.4.2 確定的有窮自動機DFA

3.4.3 不確定的有窮自動機NFA

3.4.4 NFA的確定化 子集法

3.4.5 DFA的化簡（最小化） 分割法

第二部分：

3.5 有窮自動機、正則文法、正則表示式的轉化

3.6 詞法分析程式的設計與實現

3.7 詞法分析程式的自動生成器LEX

本章總內容

重點：詞法分析介紹、詞法分析單詞種類劃分、正則文法、狀態圖、正則表示式、自動機、自動機的轉化、表示式文法和自動機的轉化、詞法分析程式的設計實現，詞法分析程式自動生成器LEX。

3.1 詞法分析程式的功能及實現方案

詞法分析程式的功能是：

1.掃描源程式字元，按語言的詞法規則識別出各類單詞符號（Token），並將有關字元組合為單詞輸出，同時進行詞法檢查；

2.對數字常數完成數字字串到（二進位制）數值的轉換；

3.刪去空格、換行、製表等字元和註釋。（例如ascii碼中的9,10,13）

通過詞法分析後便可將以字串表示的源程式加工成為以單詞表示的源程式。

實現方式基本上有兩種：

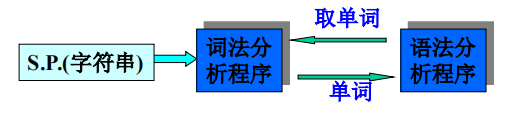
1.詞法分析單獨作為一遍，將字串轉化為單詞串，然後在下一遍中進行語法分析

2.詞法分析程式作為單獨的子程式，詞法分析程式和語法分析程式互相呼叫。

3.2 單詞的種類及詞法分析程式的輸出形式

單詞的種類

1.保留字

指語言預定義的字串，他們有固定的意義

2.識別符號

用於定義來表示各種名字的字串

3.常數

包括無符號數、布林常數、字串常數

4.分界符或操作符

可分為單字元分界符和雙字元分界符（分界符由幾個符號組成）

詞法分析程式的輸出形式，即單詞的內部形式，一般是一個二元式（單詞類別+單詞值）形式的分類是一個技術性的問題，取決於處理上的方便

1.按單詞種類分類

在劃分大分類後，統一分類下的單詞內容由確定的單詞值確定

2.保留字和分界符采用一符一類

這樣處理起來方便，因為一個類別只含一個單詞，對於這個單詞，類別編碼就代表其自身的值，不必再判斷單詞值。

3.識別符號和常數的單詞值可用指示字（指標）來表示，即識別符號在符號表中的地址和常數在常數表中的地址。

3.3 正則文法及狀態圖

很多程式設計語言的單詞都可用喬姆斯基3型文法，即正則文法描述，其描述的語言可用有窮（狀態）自動機來識別，狀態圖既是這種狀態機的非形式表示，而正則表示式則可以稱為是正則文法的化簡

3.3.1 狀態圖

狀態圖也稱狀態轉化圖，是一個有向圖。

結點表示狀態，用圓圈表示；結點之間用弧連線，弧上的標記表示弧的射出結點狀態下可能出現的輸出字元。

每個狀態圖包含有限個狀態，其中有一個初始狀態（初態）和至少一個終止狀態（終態，雙圈表示）

繪製左線性文法的狀態圖（狀態圖只能用於左線性文法，這是和後面的DFA的明顯區別）狀態圖的繪製沒有嚴格規定（右線性的暫時不做考慮）

1.文法的非終結符號是一個個的結點

2.設一開始狀態S（句子）

3.對規則Q::=t（t為終結符），需要一條從S到Q的一條弧，弧上標記為t

4.對Q::=Rt，畫一條從R到Q的弧，弧上標記為t

（倒，誰規約於誰，誰指向誰）

5.根據自動機方法，可加上開始狀態和終止狀態標誌，識別符號作終止狀態，用雙圓圈標識

3.3.2 狀態圖的使用

狀態圖構建後便可接受字串對其進行分析，分析步驟：

1.字串為初始狀態S，從其的最左字元開始重複步驟2，直到遍歷完成

2.掃描字串的下一字元，在當前狀態的向外弧中找出標記為該字元的弧，按方向切換狀態。如果沒有則說明x不是該文法的句子，當到達最後一個字元且下一個狀態為Z，則達到了終止狀態，x是該文法的合法句子。

狀態圖分析是自底向上的分析，每一步的控制代碼都是當前狀態要進入的字元，而控制代碼所要規約的符號就是下一狀態的內容。

3.4 正則表示式與有窮自動機FA

3.4.1 正則表示式

正則表示式是和正則文法等價的，均可表示正則語言，不過正則表示式更為簡潔。空集合和空字串屬於正則表示式的內容。

正則表示式的三種操作符：連線、選擇和重複，假設有兩個正則表示式e1和e2，他們表述的語言是L1和L2.則有：

連線：e1e2，他們標識的語言為L1和L2內句子的拼接，前一個是e1的句子，後一個是e2的句子

選擇：e1|e2，表示的語言為L1和L2內所有的句子

重複：e1*即表示表示式的0次到若干次的自重複連線，注意不是閉包，而是任一個e1組成的串

此時在描述一些文法時便非常方便了：

<識別符號>=字母(字母|數字)*

<數>=(ε|+|-)(數字*.數字 數字*)（.是小數點，分開兩個數字是保證小數點後有數字）

定義：正則集合

有字母表Σ，定義在Σ上的正則表示式和正則集合的遞迴表示如下：

（1）空符號串和空集都是Σ上的正則表示式，他們的正則集合分別為{ε}和空集φ

（2）任何a屬於Σ，a是Σ上的正則表示式，則其正則集合為{a}

（3）假定e1和e2都是Σ上的正則表示式，則他們所表示的正則集合分別即為對應的語言L1和L2：e1|e2也是正則表示式，對應的正則集合：L1∪L2；e1e2也是，對應的正則集合：L1L2；e1*是，正則集合為L1*，即L1的閉包。

（4）所有Σ上的正則表示式和正則集合都有1,2,3產生

正則表示式中操作符的優先順序：()優先，*最高，連線其次，|最低。注意括號的是否可省略。

正則表示式的相等也是通過判斷他們描述的語言是否相等而得出的

正則表示式也滿足一些代數規則：

單位正則表示式：εe=eε=e

交換律：e1|e2=e2|e1

結合律：e1|(e2|e3)=(e1|e2)|e3

　　　　e1(e2e3)=(e1e2)e3

分配率：e1(e2|e3)=e1e2|e2e3

　　　　(e1|e2)e3=e1e2|e2e3

此外：r*=(r|ε)*，r**=r*，(r|s)*=(r*s*)*

關於正則表示式和其他的轉換會在後續（第三章第二部分）進行講解。

如何證明兩個表示式等價：證明他們的語言相同即可。

證明例題如下：

3.4.2 確定的有窮自動機DFA

deterministic finite automaton

即狀態圖的形式化表述

DFA五元式定義：M=(S,Σ,δ,S0,Z)

S為有窮狀態集

Σ為輸入字母表

δ（dai er ta）為狀態轉換函式：

　　（S×∑ → S的對映）

　　δ(s,a) = s’ s,s’∈S，a∈Σs’是s的後繼狀態

s0為初始狀態，s0∈S（一個元素）

Z為終止狀態集。Z是S子集

按順序就是五個值

狀態轉移函式可用矩陣表示：

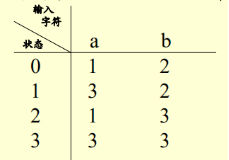，0遇到a變為1，0遇到b變為2，等

確定的有窮自動機即狀態轉換函式是單值函式，不接受ε。

一個DFA也可用一個狀態轉換圖表示：（幾個單值函式狀態圖中的弧的數量就是幾個加一，有一個start）

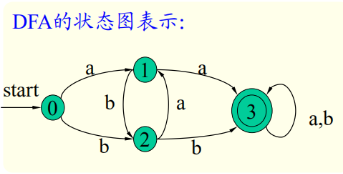
DFA接受的符號串：

對α=a1a2a3...an，α屬於Σ*

如果δ(sn-1,an) = sn，sn∈Z，則有δ(s0,α) = sn，即α可被M接受

測試分析時右側的α可以是一個完整的符號串，然後從左遞減到ε，得出的狀態如果是S則接受，否則不接受。

即如果存在一條從初始狀態到一個終止咋混個臺的路徑，該路徑上所有弧的標記符連線成符號串α，則稱α可誒DFA M接受。

對文法M接受的語言為：{α|δ(s0,α)=sn,sn∈Z}

描述語言時正式一點需要用∪符號，而不是或，集合∪即可。

3.4.3 不確定的有窮自動機NFA

NFA的五元式：M’=(S,Σ∪ε,δ,S0,Z)

區別：

輸入可為ε

狀態轉換函式修改為：（S×∑∪{ε} → 2^S的對映，2^S：S的冪集，即S的子集構成的集合）狀態轉換函式是一個多值函式，且輸入允許為ε，即對於某個輸入字元存在多個後繼狀態。

初始狀態變為一個集合，不只有一個初始狀態。（不是無意大寫的）

對文法M’所接受的語言為：L(M′)={α|δ(s0,α)=S’ S’∩Z≠Φ}

α推出的狀態集一定需要包含終止狀態，除了終止狀態也可以有其他狀態。

例：

為空即是狀態1不會遇到符號b

狀態圖：（弧數同樣為單值函式的數量加一，{2,3}相當於兩個單值函式）

有ε弧，一個狀態有多個射出弧

其接受的語言為：R=aa*b|ac*c|ε

總結：

1.正則表示式和有窮自動機

　　3型文法所定義的語言都可以用正則表示式描述

　　用正則表示式描述單詞是為了協助生成詞法分析程式

　　有一個正則表示式則對應一個正則集合

　　若V是正則集合，當且僅當V等於一個M的語言，即一個正則表示式對應一個DFA M。

2.NFA：相比DFA狀態轉換函式非單值、有ε弧。

3.4.4 NFA的確定化 子集法

利用子集法，根據定義可知，DFA和NFA從功能上是等價的的，即對NFA的M’可以構造出DFA的M，且他們構成的語言相同。

定義：集合I的ε-閉包（ε-closure(I)）

令I是一個狀態集的子集

1.如果s∈I，則s屬於I的ε閉包

2.如果s∈I，則從s出發經過任意條ε弧能夠到達的任何狀態都屬於I的ε閉包。

例：

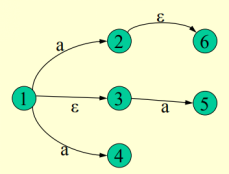
此時I為{1}，則I的ε閉包：{1,3}，1一定是，3是經過一個ε弧到達的狀態。

定義：令I是NFA M’中狀態集的一個自己，a∈Σ

J是從I中每一個狀態出發，經過標記為a的弧（任意長度）能達到的J的集合，Ia是狀態子集，即J的ε閉包。

例：

此時便可基於這兩個定義進行NFA的確定化：

確定最初的狀態子集I（開始狀態的ε閉包）

基於I分別對ε外的符號進行求Ia（Ia即Ia,Ib,Ic等等所有魚符號），求出後如果不為空且不重複，則在下一步對不為空的Ia作為I再次對ε之外的符號求Ia。直到沒有新出現的狀態子集。

例如：

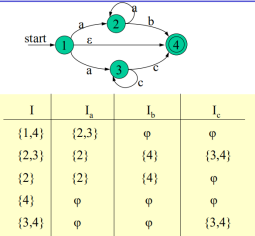
此時可將所有的狀態子集進行變化：

該矩陣既是一個新的狀態轉換矩陣，對其重新編號既得轉化為的DFA M狀態轉換矩陣：

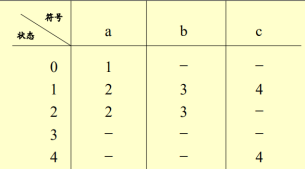
再畫出新的狀態圖即可：

DFA M的初態：原初始狀態1的ε閉包（找出新狀態中哪個是1的ε閉包，它既是DFA M初態）

終態：包含終止狀態4的狀態子集（可有多個，即推導過程中包含狀態4的狀態子集）

3.4.5 DFA的化簡（最小化） 分割法

定理：對任一DFA，都存在一個唯一的狀態最少的等價的DFA

這個DFA稱為化簡的，充要條件為：沒有多餘狀態且它的狀態中沒有兩個是互相等價的。

最小化：即通過消除多餘狀態和合並等價狀態實現

（1）多餘狀態：從開始狀態開始，任何輸入串也到達不了的狀態（可用狀態圖輔助尋找）

（2）等價狀態，對s和t，他們的等價條件：

1.一致性條件：s和t必須同時為可接受狀態或不接受狀態（必須同時為終止狀態或者不是終止狀態）

2.蔓延性條件：對所有輸入符號，s和t都轉換到等價的狀態裡（最後會合並）

簡易判斷：對所有輸入符號c，如果Ic(s)=Ic(t)，即狀態s和t對c具有相同的後繼，則他們是等價的。（Ic(s)的符號意義：）

（注：任何有後繼的狀態和任何無後繼的狀態一定不等價，不等價即是可區別的）

轉換方法：分割法，把DFA的狀態不斷分割為不相關的子集，任何兩個不同子集的狀態都是可區別的，而同一個子集中的任何狀態都等價。

例：

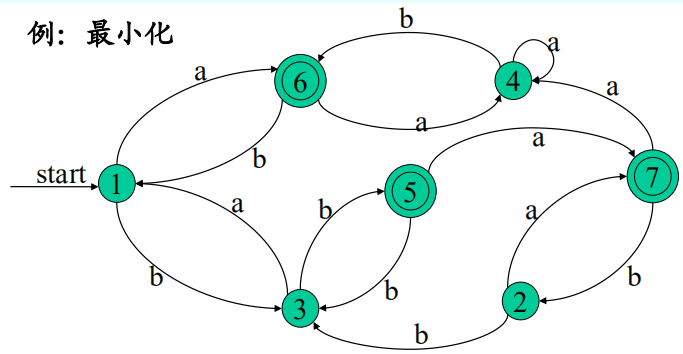
構建：所有狀態放左側，輸入字元在上方，轉化矩陣依據初態和輸入構建，開始狀態知道即可，終止狀態也記住。

利用一致性條件：將終態和非終態區分開並標號

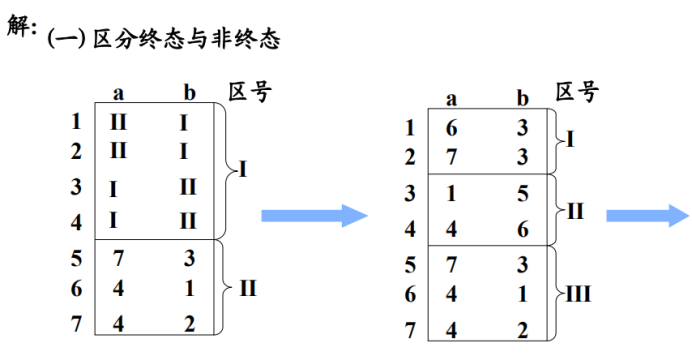
然後不斷根據蔓延性條件：判斷一個區內的幾個狀態，當他們遇到符號後進入的區的區號是否相等，將相等的重新劃為一個區。

重新劃分後再依次判斷每個區是否能再次區分開，直到全部無法再劃分即可結束，結束即將區號轉為狀態重新形成DFA即可。

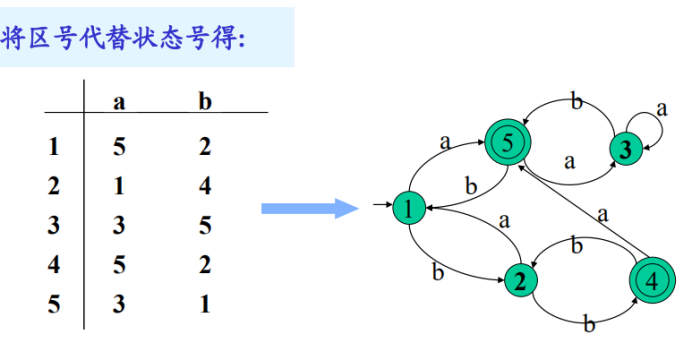
剩下的內容

有窮自動機、正則文法、正則表示式的轉化，詞法分析程式的設計與實現和詞法分析程式的自動生成器LEX會在第三章的第二部分進行介