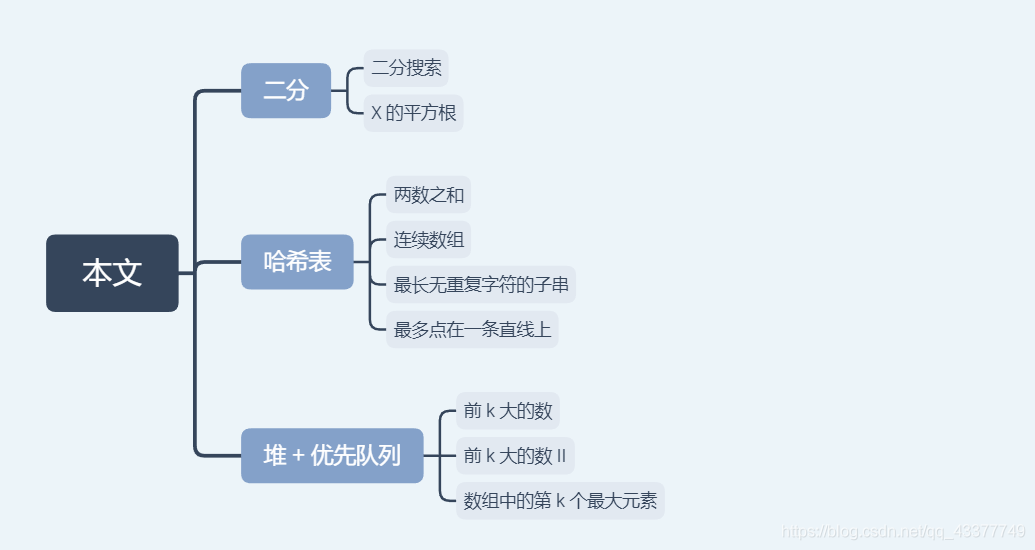
面試高頻演算法題彙總「圖文解析 + 教學視訊 + 範例程式碼」之 二分 + 雜湊表 + 堆 + 優先佇列 合集
本文將覆蓋 二分 + 雜湊表 + 堆 + 優先佇列 方面的面試演算法題,文中我將給出:
- 面試中的題目
- 解題的思路
- 特定問題的技巧和注意事項
- 考察的知識點及其概念
- 詳細的程式碼和解析
在開始之前,我們先看下會有哪些重點內容:
現在就讓我們開始吧!
二分
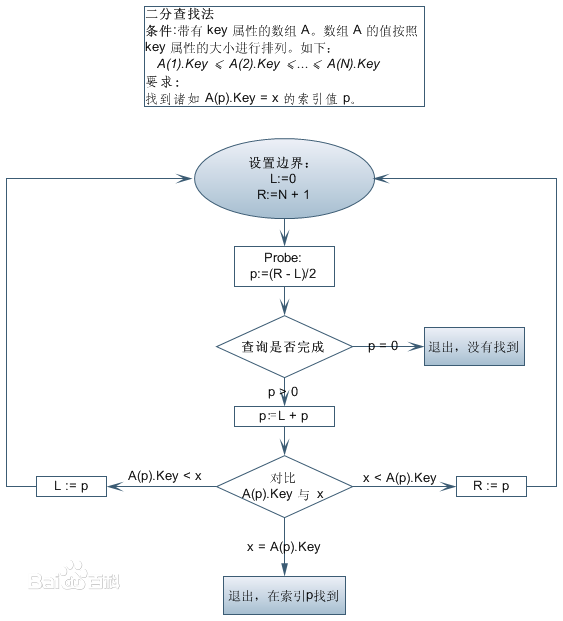
概念:
二分查詢也稱折半查詢(Binary Search),它是一種效率較高的查詢方法。但是,折半查詢要求線性表必須採用順序儲存結構,而且表中元素按關鍵字有序排列。- 基本思路:
- 首先,假設表中元素是按升序排列,將表中間位置記錄的關鍵字與查詢關鍵字比較
- 如果兩者相等,則查詢成功
- 否則利用中間位置記錄將表分成前、後兩個子表
- 如果中間位置記錄的關鍵字大於查詢關鍵字,則進一步查詢前一子表
- 否則進一步查詢後一子表
- 重複以上過程,直到找到滿足條件的記錄,使查詢成功,或直到子表不存在為止,此時查詢不成功。
二分搜尋
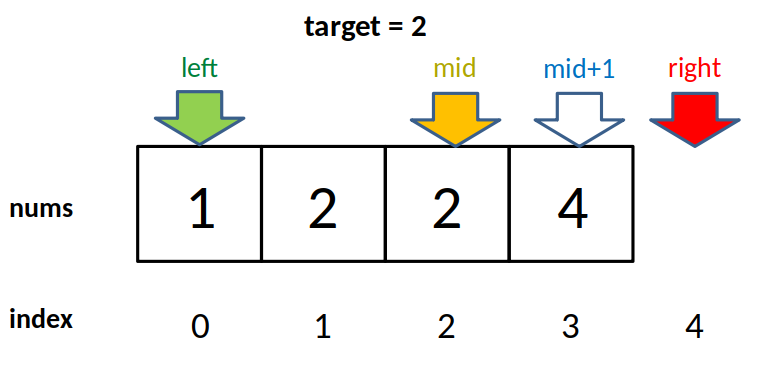
給定一個 n 個元素有序的(升序)整型陣列 nums 和一個目標值 target ,寫一個函式搜尋 nums 中的 target,如果目標值存在返回下標,否則返回 -1。
示例 1:
輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中並且下標為 4
技巧:
分析二分查詢的一個技巧是:
- 不要出現 else,而是把所有情況用
if/else if寫清楚 - 這樣可以清楚地展現所有細節。
這裡我們以遞迴和非遞迴方式,解決面試中的二分搜尋題
遞迴
思路很簡單:
- 判斷起始點是否大於終止點
- 比較
nums[mid]與目標值大小 - 如果
nums[mid]大,說明目標值 target 在前面 - 反之如果
nums[mid]小,說明目標值 target 在前面後面 - 如果既不大也不小,說明相等,則返回
當前位置
class Solution { public int search(int[] nums, int target) { return binarySearch(nums, 0, nums.length - 1, target); } private int binarySearch(int[] nums, int start, int end, int target) { if(start > end) { return -1; } int mid = (end + start) / 2; if(nums[mid] < target) { return binarySearch(nums, mid + 1, end, target); } if(nums[mid] > target) { return binarySearch(nums, start, mid - 1, target); } return mid; } }
非遞迴
這個場景是最簡單的:
- 搜尋一個數
- 如果存在, 返回其索引
- 否則返回 -1
int binarySearch(int[] nums, int target) {
int left = 0;
// 注意減 1
int right = nums.length - 1;
while(left <= right) {
int mid = (right + left) / 2;
if(nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1; // 注意
else if (nums[mid] > target)
right = mid - 1; // 注意
}
return -1;
}相關視訊
分鐘教你二分查詢(python版)
X的平方根
計算並返回 x 的平方根,其中 x 是非負整數。
由於返回型別是整數,結果只保留整數的部分,小數部分將被捨去。
示例 2:
輸入: 8
輸出: 2
說明: 8 的平方根是 2.82842...,
由於返回型別是整數,小數部分將被捨去。
解題思路
使用二分法搜尋平方根的思想很簡單:
- 就類似於小時候我們看的電視節目中的“猜價格”遊戲
- 高了就往低了猜
- 低了就往高了猜
- 範圍越來越小。
注:一個數的平方根最多不會超過它的一半,例如 8 的平方根,8 的一半是 4,如果這個數越大越是如此
注意:
對於判斷條件:
- 比如說:我們很容易想當然覺得
mid == x / mid和mid * mid == x是等價的,實際卻不然- 比如 mid = 2,x = 5
- 對於
mid == x / mid就是:2 == 2 返回 true - 而對於
mid * mid == x就是:4 == 5 返回 false
對於邊界條件有個坑:
- 要注意此處耍了一下小技巧,在二分左值和右值相差為1的時候就停止查詢;因為在這裡,有個對中值取整數的操作,在取整後始終有
start==mid==end則會死迴圈。
取整操作的誤差為1,故而在這裡限制條件改成包含1在內的範圍start + 1 < end ; 這裡減一很精髓
public int sqrt(int x) {
if (x < 0) {
throw new IllegalArgumentException();
} else if (x <= 1) {
return x;
}
int start = 1, end = x;
// 直接對答案可能存在的區間進行二分 => 二分答案
while (start + 1 < end) {
int mid = start + (end - start) / 2;
if (mid == x / mid) {
return mid;
} else if (mid < x / mid) {
start = mid;
} else {
end = mid;
}
}
if (end > x / end) {
return start;
}
return end;
}
雜湊表
概念
散列表(Hash table,也叫雜湊表),是根據關鍵碼值(Key value)而直接進行訪問的資料結構。也就是說,它通過把關鍵碼值對映到表中一個位置來訪問記錄,以加快查詢的速度。這個對映函式叫做雜湊函式,存放記錄的陣列叫做散列表。資料結構
給定表M,存在函式f(key),對任意給定的關鍵字值key,代入函式後若能得到包含該關鍵字的記錄在表中的地址,則稱表M為雜湊(Hash)表,函式f(key)為雜湊(Hash) 函式。
兩數之和
給一個整數陣列,找到兩個數使得他們的和等於一個給定的數 target。需要實現的函式 twoSum 需要返回這兩個數的下標。
示例:
給定
nums = [2, 7, 11, 15], target = 9因為
nums[0] + nums[1] = 2 + 7 = 9
所以返回[0, 1]
解題思路
- 用一個
hashmap來記錄 key記錄target - numbers[i]的值,value記錄numbers[i]的i的值- 如果碰到一個
numbers[j]在hashmap中存在 - 那麼說明前面的某個
numbers[i]和numbers[j]的和為target - 那麼當前的
i和j即為答案
public int[] twoSum(int[] numbers, int target) {
HashMap<Integer,Integer> map = new HashMap<>();
for (int i = 0; i < numbers.length; i++) {
// 判斷 map 中是否有需要該值的項
if (map.containsKey(numbers[i])) {
return new int[]{map.get(numbers[i]), i};
}
// 意思可理解為第 i 項,需要 target - numbers[i]
map.put(target - numbers[i], i);
}
return new int[]{};
}
連續陣列
給一個二進位制陣列,找到 0 和 1 數量相等的子陣列的最大長度
示例 2:
輸入: [0,1,0]
輸出: 2
說明: [0, 1] (或 [1, 0]) 是具有相同數量0和1的最長連續子陣列。
步驟
使用一個數字
sum維護到i為止1的數量與0的數量的差值在
loop i的同時維護sum並將其插入hashmap中對於某一個sum值,若hashmap中已有這個值
則當前的
i與sum上一次出現的位置之間的序列0的數量與1的數量相同
public int findMaxLength(int[] nums) {
Map<Integer, Integer> prefix = new HashMap<>();
int sum = 0;
int max = 0;
// 因為在開始時 0 、 1 的數量都為 0 ,所以必須先存 0
// 否則第一次為 0 的時候,<- i - prefix.get(sum) -> 找不到 prefix.get(0)
prefix.put(0, -1);
// 當第一個 0 1 數量相等的情況出現時,陣列下標減去-1得到正確的長度
for (int i = 0; i < nums.length; i++) {
int num = nums[i];
if (num == 0) {
sum--;
} else {
sum++;
}
// 判斷是否已存在 sum 值
// 存在則說明之前存過
if (prefix.containsKey(sum)) {
// 只做判斷,不做儲存
max = Math.max(max, i - prefix.get(sum));
} else {
prefix.put(sum, i);
}
}
return max;
}
最長無重複字元的子串
給定一個字串,請你找出其中不含有重複字元的 最長子串 的長度。
輸入: "abcabcbb"
輸出: 3
解釋: 因為無重複字元的最長子串是 "abc",所以其長度為 3。
解題思路
用HashMap記錄每一個字母出現的位置:
- 設定一個
左邊界,到當前列舉到的位置之間的字串為不含重複字元的子串。 - 若新碰到的字元的上一次的位置在左邊界右邊, 則需要向右移動左邊界。
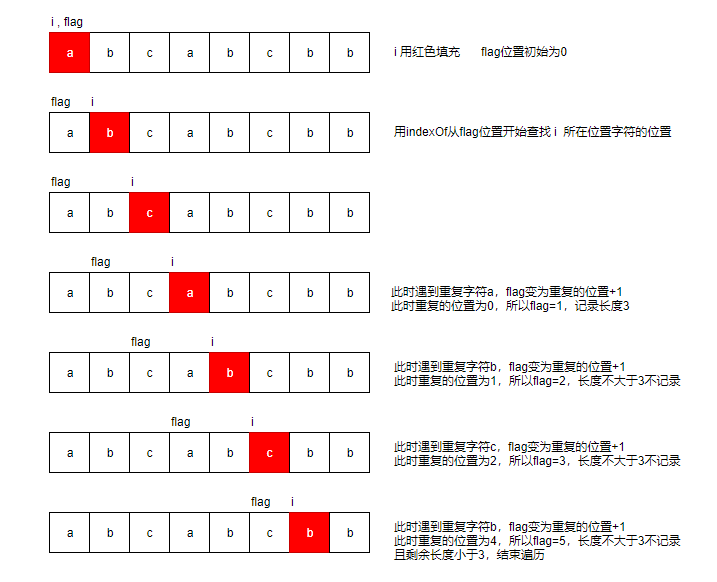
視訊
大聖演算法- 最長無重複字元的子串
public int lengthOfLongestSubstring(String s) {
if (s == null || s.length() == 0) {
return 0;
}
HashMap<Character, Integer> map = new HashMap<>();
int max = Integer.MIN_VALUE;
// 計算無重複字元子串開始的位置
int start = -1;
int current = 0;
for (int i = 0; i < s.length(); i++) {
if (map.containsKey(s.charAt(i))) {
int tmp = map.get(s.charAt(i));
// 上一次的位置在左邊界右邊, 則需要向右移動左邊界
if (tmp >= start) {
start = tmp;
}
}
map.put(s.charAt(i), i);
max = Math.max(max, i - start);
}
return max;
}
最多點在一條直線上
給出二維平面上的n個點,求最多有多少點在同一條直線上
首先點的定義如下
class Point { int x; int y; Point() { x = 0; y = 0; } Point(int a, int b) { x = a; y = b; } }示例 :
輸入: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
輸出: 4
解釋:
^
|
| o
| o o
| o
| o o
+------------------->
0 1 2 3 4 5 6
解題思路
提示:我們會發現,其實只需要考慮當前點之後出現的點i + 1 .. N - 1即可,因為通過點 i-2 的直線已經在搜尋點 i-2 的過程中考慮過了。
畫一條通過點 i 和
之後出現的點的直線,在雜湊表中儲存這條邊並計數為2= 當前這條直線上有兩個點。儲存時,以斜率來區分線與線之間的關係
假設現在
i<i + k<i + l這三個點在同一條直線上,當畫出一條通過 i 和 i+l 的直線會發現已經記錄過了,因此對更新這條邊對應的計數:count++。
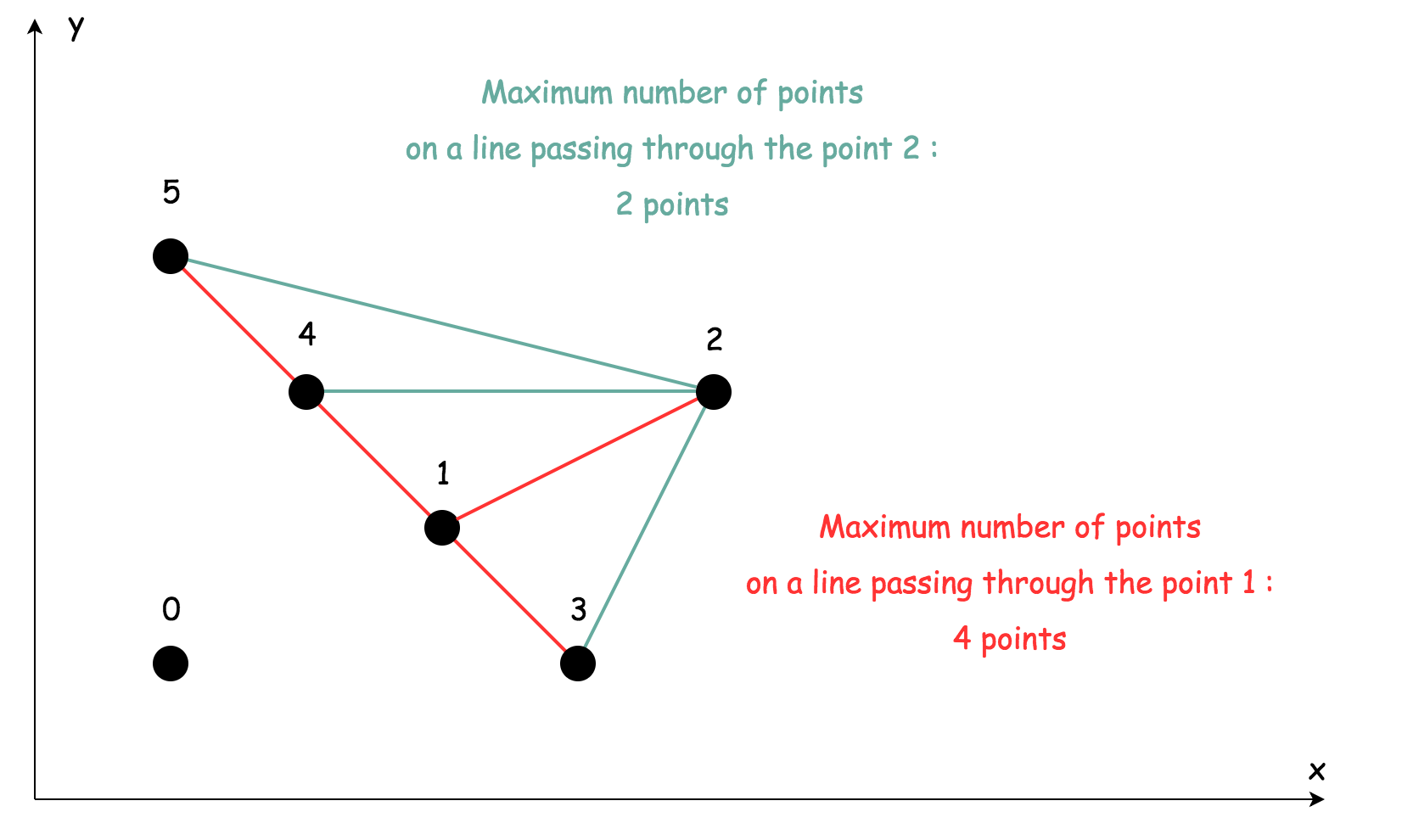
通過 HashMap 記錄下兩個點之間的斜率相同出現的次數,注意考慮點重合的情況
public int maxPoints(int[][] points) {
if (points == null) {
return 0;
}
int max = 0;
for (int i = 0; i < points.length; i++) {
Map<String, Integer> map = new HashMap<>();
int maxPoints = 0;
int overlap = 0;
for (int j = i + 1; j < points.length; j++) {
int dy = points[i][1] - points[j][1];
int dx = points[i][0] - points[j][0];
// 兩個點重合的情況記錄下來
if (dy == 0 && dx == 0) {
overlap++;
continue;
}
// 防止 x 相同 y 不同,但 rate 都為 0
// 防止 y 相同 x 不同,但 rate 都為 0
// 以及超大數約等於 0 的情況:[[0,0],[94911151,94911150],[94911152,94911151]]
String rate = "";
if(dy == 0)
rate = "yy";
else if (dx == 0)
rate = "xx";
else
rate = ((dy * 1.0) / dx) + "";
map.put(rate, map.getOrDefault(rate, 0) + 1);
maxPoints = Math.max(maxPoints, map.get(rate));
}
max = Math.max(max, overlap + maxPoints + 1);
}
return max;
}堆 / 優先佇列
- 堆(英語:heap)是電腦科學中一類特殊的資料結構的統稱。將根節點最大的堆叫做最大堆或大根堆,根節點最小的堆叫做最小堆或小根堆。
堆通常是一個可以被看做一棵樹的陣列物件。堆總是滿足下列性質:
- 堆中某個節點的值總是不大於或不小於其父節點的值;
- 堆總是一棵完全二叉樹。
如下圖這是一個最大堆,,因為每一個父節點的值都比其子節點要大。10 比 7 和 2 都大。7 比 5 和 1都大。
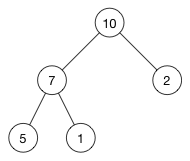
- 優先佇列(priority queue)
優先佇列是一種抽象資料型別,它是一種排序的機制,它有兩個核心操作:找出鍵值最大(優先順序最高)的元素、插入新的元素,效果就是他在維護一個動態的佇列。可以收集一些元素,並快速取出鍵值最大的元素,對其操作後移出佇列,然後再收集更多的元素,再處理當前鍵值最大的元素,如此這般。 - 例如,我們有一臺能夠執行多個程式的計算機。計算機通過給每個應用一個優先順序屬性,將應用根據優先順序進行排列,計算機總是處理下一個優先順序最高的元素。
前K大的數
PriorityQueue 優先佇列:Java 的優先佇列,保證了每次取最小元素
// 維護一個 PriorityQueue,以返回前K大的數
public int[] topk(int[] nums, int k) {
int[] result = new int[k];
if (nums == null || nums.length < k) {
return result;
}
Queue<Integer> pq = new PriorityQueue<>();
for (int num : nums) {
pq.add(num);
if (pq.size() > k) {
// poll() 方法用於檢索或獲取和刪除佇列的第一個元素或佇列頭部的元素
pq.poll();
}
}
for (int i = k - 1; i >= 0; i--) {
result[i] = pq.poll();
}
return result;
}前K大的數II
實現一個數據結構,提供下面兩個介面:
- add(number) 新增一個元素
- topk() 返回前K大的數
public class Solution {
private int maxSize;
private Queue<Integer> minheap;
public Solution(int k) {
minheap = new PriorityQueue<>();
maxSize = k;
}
public void add(int num) {
if (minheap.size() < maxSize) {
// add(E e)和offer(E e)的語義相同,都是向優先佇列中插入元素
// 只是Queue介面規定二者對插入失敗時的處理不同
// 前者在插入失敗時丟擲異常,後則則會返回false
minheap.offer(num);
return;
}
if (num > minheap.peek()) {
minheap.poll();
minheap.offer(num);
}
}
public List<Integer> topk() {
// 將佇列中的數存到陣列中
Iterator it = minheap.iterator();
List<Integer> result = new ArrayList<Integer>();
while (it.hasNext()) {
result.add((Integer) it.next());
}
// 呼叫陣列排序法後返回
Collections.sort(result, Collections.reverseOrder());
return result;
}
}陣列中的第K個最大元素
在未排序的陣列中找到第 k 個最大的元素。請注意,你需要找的是陣列排序後的第 k 個最大的元素,而不是第 k 個不同的元素。
示例 2:
輸入: [3,2,3,1,2,4,5,5,6] 和 k = 4
輸出: 4
我的第一個想法:暴力法
public int findKthLargest(int[] nums, int k) {
Queue<Integer> que = new PriorityQueue<>();
for(int num : nums) {
if(que.size() < k) {
que.offer(num);
} else {
if(que.peek() < num) {
que.poll();
que.offer(num);
}
}
}
return que.peek();
}這裡舉個無關的演算法:
使用快速排序,思路極其簡單:
- 首先對陣列進行快速排序
- 最後返回
第 k 個數即可

具體實現:
public int kthLargestElement(int k, int[] nums) {
if (nums == null || nums.length == 0 || k < 1 || k > nums.length){
return -1;
}
return partition(nums, 0, nums.length - 1, nums.length - k);
}
private int partition(int[] nums, int start, int end, int k) {
if (start >= end) {
return nums[k];
}
int left = start, right = end;
int pivot = nums[(start + end) / 2];
while (left <= right) {
while (left <= right && nums[left] < pivot) {
left++;
}
while (left <= right && nums[right] > pivot) {
right--;
}
if (left <= right) {
swap(nums, left, right);
left++;
right--;
}
}
if (k <= right) {
return partition(nums, start, right, k);
}
if (k >= left) {
return partition(nums, left, end, k);
}
return nums[k];
}
private void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
Attention
為了提高文章質量,防止冗長乏味
下一部分演算法題
本片文章篇幅總結越長。我一直覺得,一片過長的文章,就像一場超長的 會議/課堂,體驗很不好,所以打算再開一篇文章來總結其餘的考點
在後續文章中,我將繼續針對
連結串列棧佇列堆動態規劃矩陣位運算等近百種,面試高頻演算法題,及其圖文解析 + 教學視訊 + 範例程式碼,進行深入剖析有興趣可以繼續關注 _yuanhao 的程式設計世界
