回聲消除中的自適應演算法發展歷程

阿新 • • 發佈：2019-11-02

　　傳統的IIR和FIR濾波器在處理輸入訊號的過程中濾波器的引數固定，當環境發生變化時，濾波器無法實現原先設定的目標。自適應濾波器能夠根據自身的狀態和環境變化調整濾波器的權重。

自適應濾波器理論

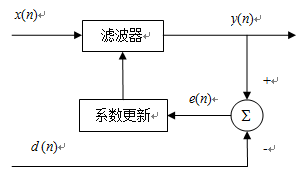
　　$x(n)$是輸入訊號，$y(n)$是輸出訊號，$d(n)$是期望訊號或參考訊號，$e(n)=d(n)-y(n)$為誤差訊號。根據自適應演算法和誤差訊號$e(n)$調整濾波器係數。

　　自適應濾波器型別。可以分為兩大類：非線性自適應濾波器、線性自適應濾波器。非線性自適應濾波器包括基於神經網路的自適應濾波器及Volterra濾波器。非線性自適應濾波器訊號處理能力更強，但計算複雜度較高。所以實踐中，線性自適應濾波器使用較多。

自適應濾波器結構

主要分為兩類FIR濾波器、IIR濾波器。

FIR濾波器時非遞迴系統，即當前輸出樣本僅是過去和現在輸入樣本的函式，其系統衝激響應h(n)是一個有限長序列。具有很好的線性相位，無相位失真，穩定性較好。
IIR濾波器時遞迴系統，即當前輸出樣本是過去輸出和過去輸入樣本的函式，其系統衝激h(n)是一個無限長序列。IIR系統的相頻特性是非線性的，穩定性不能保證。好處是實現階數較低，計算量較少。

　　自適應濾波器演算法按照不同的優化準則，常見自適應濾波演算法有：遞推最小二乘演算法(RLS)，最小均方誤差演算法(LMS)，歸一化均方誤差演算法(NLMS)，快速精確最小均方誤差演算法，子帶濾波，頻域的自適應濾波等等。

效能指標

收斂速度
穩定性
計算複雜度

全帶自適應稀疏演算法

最小均方演算法 LMS

自適應AEC問題中應用最廣泛的就是自適應濾波演算法，其中最早是由Widrow和Hoff在1959年所提出的最小均方（Least Mean Square，LMS）演算法

LMS演算法基於維納濾波理論，採用最速下降演算法，通過最小化誤差訊號的能量來更新自適應濾波器權值係數。

優點：抑制旁瓣效應
缺點：LMS演算法計算複雜度不高，但是其收斂速率較慢，並且隨著濾波器階數(步長引數)升高，系統的穩定性下降，要保證採用最小的步長引數，保證最小的失調，可能無法滿足收斂標準

歸一化最小均方演算法 NLMS

　　歸一化最小均方(Normalized Least Mean Squares，==NLMS)==演算法是改進的LMS演算法，根據原LMS演算法中誤差訊號與遠端輸入訊號的乘積，對遠端輸入訊號的平方歐式範數進行歸一化處理，將固定步長因子的LMS演算法變為根據輸入訊號時變的變步長NLMS演算法，

優點：改善了LMS演算法收斂速度慢的缺點。計算簡單、收斂速度較快的特點
缺點：收斂速度慢

變步長LMS

優點：收斂速度快，

缺點：演算法的穩定性和跟蹤能力上較易受輸入噪聲的影響

仿射投影演算法

稀疏類自適應演算法

通過對回聲路徑模型的分析，發現回聲能量中較活躍係數均在時域聚集，且比重很小，其數值只有很少不為零的有效值，大多數都是零值或者接近零值，這就是回聲路徑具有的稀疏特性

PNLMS

根據回聲路徑的稀疏性，Duttweiler引入了比例自適應的思想，提出了比例歸一化最小均方演算法 PNLMS，按比例分配濾波器的權值向量大小，該演算法對回聲消除的發展具有非常重要的意義。

　　該演算法採用與濾波器抽頭稀疏成正比的可變步長引數來調整演算法收斂速度，利用其抽頭稀疏的比例值來判斷當前權重稀疏所屬的活躍狀態，根據狀態的不同，所分配的步長大小也有所差異，活躍抽頭係數分配較大的步長引數，這樣可以加速其收斂，而不活躍的抽頭係數則相反，通過分配其較小的步長引數來提高演算法的穩態誤差。每個濾波器抽頭被分別賦予了不同估計值，演算法的穩態收斂性得到了明顯改善。然而，PNLMS 有一個明顯的缺點，即比例步長引數的選擇引入了定值，這會導致估計誤差累積，最後使演算法在後期的收斂速度減慢下來。

優點：使演算法對於稀疏的回聲路徑，在初始階段擁有快速的收斂速率，與此同時降低了穩態誤差，
缺點：

由於 PNLMS 演算法過分強調大系數的收斂，而當係數變小後，P 步長也隨之變小，但隨著演算法的執行，則可能出現演算法後期收斂速度慢、不能及時收斂的情況
相比於NLMS演算法增加了演算法的複雜度
另外在回聲路徑非稀疏情況下，收斂速度會變得比NLMS演算法更慢

PNLMS++

PNLMS ++演算法，在每個取樣週期內，通過將NLMS演算法和PNLMS演算法之間進行交替來實現收斂速度方面的提升。但是PNLMS ++演算法只在回聲路徑稀疏或高度非稀疏的情況下表現良好。

CPNLMS

CPNLMS 演算法（Composite PNLMS）通過比較誤差訊號功率和已設閾值大小，來判斷演算法採用 PNLMS 還是 NLMS 演算法

缺點：閾值的選取往往和實際環境有關，因此該演算法在實際應用中不能通用

$\mu$準則MPNLMS

$\mu$準則MPNLMS演算法：為了解決PNLMS演算法後程收斂速度慢的問題，將最速下降法應用到PNLMS演算法中，使用$\mu$準則來計算比例因子（使用對數函式代替PNLMS演算法中的絕對值函式）

優點：使得濾波器權值向量的更新更加平衡，提升了PNLMS演算法接近穩態時期的收斂速率
缺點：複雜性加大

改進比例歸一化最小均方 IPNLMS

　　IPNLMS演算法，基於L1範數將估計的回聲路徑權值向量均值與比例步長引數之和作為比例矩陣的對角元素（通過調整濾波器的比例引數步長），使得IPNLMS有著和PNLMS相近的初始收斂速率，並且在非稀疏的回聲路徑條件下，IPNLMS的收斂速率相比PNLMS有所改善，但效能改善的同時也增加了計算複雜度。

改進的IPNLMS

　　在PNLMS類演算法進行自適應迭代更新過程中，大抽頭權值向量擁有大步長因子，這樣提升了收斂速率，但濾波器自適應收斂至接近穩態時，大抽頭權值向量將會產生較大的穩態誤差。為了解決這一問題，P.A.Naylor提出了改進的IPNLMS（Improved IPNLMS，IIPNLMS）演算法。IIPNLMS演算法在IPNLMS演算法的基礎之上，對於數值較大的權值向量，使用較小的引數使得其步長成比例減小，從而降低係數噪聲。

MPNLMS

MPNLMS演算法引入最優步長控制矩陣，均衡了濾波器大小系數之間的更新，修正了 PNLMS 演算法收斂後期速度慢的缺點，但

缺點：MPNLMS演算法的運算過程中包含對數的計算，因此演算法的運算複雜度相對較高。

SPNLMS

SPNLMS演算法，將MPNLMS濾波器更新過程中的對數運算化簡為兩段簡單函式的形式。

優點：相對於MPNLMS為減小運法複雜度

改進的 MPNLMS演算法，採用多個分段函式來近似 MPNLMS 的對數函式，從而降低演算法的複雜度。

改進的 SPNLMS演算法，通過控制步長控制矩陣迭代的頻率降低演算法複雜度。收斂速度也所下降

以上對 MPNLMS 的改進演算法在減小演算法運算複雜度的情況下損害了收斂效能和穩定效能。

稀疏控制(Sparse Control, SC)

有時候回聲路徑的稀疏程度會根據溫度、壓力以及房間牆面的吸聲係數等等因素而產生變化，這就需要一種能夠適應不同稀疏度變化的AEC演算法。

稀疏控制比例回聲消除演算法（SC-PNLMS、SC-MPLNMS、SC-IPNLMS），使用新的稀疏控制方法動態地適應回聲路徑的稀疏程度，使得演算法在稀疏和非稀疏的回聲路徑條件下都有良好的效能表現，體現了稀疏控制類的自適應濾波演算法能夠提高演算法對回聲路徑稀疏程度的魯棒性。

小總結：通過上述對 PNLMS 演算法的分析，可知導致 PNLMS 演算法整體收斂速度慢的原因主要是大系數和小系數之間收斂的不均衡。儘管很多學者針對此缺陷提出了修正演算法，如 PNLMS++、CPNLMS 等，但是 PNLMS 忽略小系數收斂的缺陷並未從根本上得到改善，因此這些改進演算法的效果不是十分理想。Deng通過對濾波器係數收斂過程的定量分析，在權係數更新過程中推匯出最優步長的計算方式，提出一種改進的演算法——MPNLMS 演算法。MPNLMS 中 P 步長的計算方式克服了 PNLMS 過分注重大系數收斂忽略小系數收斂的缺點，修正了 PNLMS 收斂後期速度慢的缺陷。

　　一種新的改進型 PNLMS 演算法，因 PNLMS 演算法只注重大系數更新，忽視小系數收斂，致使演算法在收斂後期速度下降，因此在 P 步長引入的同時必須注意小系數的更新。MPNLMS 演算法通過建立 P 步長與當前濾波器權係數的函式關係，在一定程度上解決了 PNLMS 演算法後期收斂速度慢的問題，但濾波過程包含了對數運算，不利於系統的實時實現。

　　本文通過定量分析濾波過程，並考慮到大、小系數的收斂，建立了一種新的 P步長與當前濾波器係數之間的對映關係，降低了演算法的運算複雜度。該改進演算法以 PNLMS 演算法為基礎，通過改變收斂過程來克服 PNLMS 演算法的缺陷

子帶自適應濾波器

　　在聲學回聲消除應用中，遠端輸入語音訊號的相關性較高，然而，傳統的方法是基於“訊號的無關性”假設的，傳統的全帶LMS 和NLMS 等計算複雜度低的隨機梯度演算法收斂速度明顯下降。

遠端語音訊號相關性有兩層含義：

時域上：它表徵語音訊號相關矩陣特徵值的擴散度
頻域上：它表徵遠端語音訊號的頻譜動態範圍

　　一般來說，語音訊號相比白色訊號，前者明顯有更大的頻譜動態範圍，即更大的訊號相關性。因此，可以通過降低輸入訊號的相關性來加快演算法收斂速度，但是行之有效的一種方法是將自適應濾波器和濾波器組理論相結合，提出了子帶自適應濾波（subband adaptive filter，SAF）演算法，

子帶自適應濾波器：SAF演算法將相關訊號通過濾波器組分割成近似無關的各個子帶獨立訊號(子帶分割)。然後對子帶訊號進行多速率抽取來獲得取樣訊號，再進行訊號的自適應處理。為研究子帶自適應濾波器，首先需要了解多速率訊號抽取系統和濾波器組。

多速率系統^[1]

　　用於子帶自適應濾波器的多速率抽取系統有下采樣和上取樣兩種，主要通過抽取和插值方法來使系統獲得不同取樣率。輸入訊號經過 N 個濾波器分頻後的總取樣點數是原訊號的 N 倍，大幅度提高的取樣數增加了計算量。

濾波器組^[1]

　　訊號子帶分割通過濾波器組實現。濾波器組由分析濾波器和綜合濾波器共同組成。而濾波器組的實質是一系列帶通濾波器。

　　分析濾波器組將數字訊號分割後抽取成多個子帶訊號，經過訊號處理後，綜合濾波器組再對子帶訊號進行插值和濾波相加而恢復成原來的訊號。

子帶自適應演算法結構^[1]

　　在傳統的 SAF中，子帶自適應演算法都是以最小化子帶誤差訊號為目標的，這樣基於區域性目標函式誤差的最小化不一定是全域性誤差能量最小化。而分析濾波器組在子帶切割和綜合濾波器組重建全帶訊號時皆會引入時延，在AEC 應用中，這樣的時延會使包含近端語音的全帶誤差訊號傳到遠端，為了消除時延的影響，無延時子帶閉環結構系統以全域性誤差能量最小化為約束條件來調整濾波器係數。最後，確保自適應濾波演算法能夠收斂到最佳的濾波器係數。

優點：改善了全帶自適應濾波演算法在相關訊號條件下的收斂速率
缺點：
- 但其穩態誤差由於輸出時存在的混疊分量而顯著升高
- 當採用正交映象濾波器組時，雖然可以通過子帶系統將混疊部分相互抵消掉，但在現實中卻無法實現

子帶自適應演算法的後續發展

問題：針對SAF演算法穩態誤差較高的問題

解決：提出了基於最小擾動原理提出了歸一化的SAF（normalized SAF，NSAF）演算法。

優點：由於SAF類演算法固有的解相關特性，NSAF在處理相關輸入訊號時比全帶的NLMS收斂速度快，而且計算成本與NLMS不相上下

近幾年研究人員為了能夠提升AEC演算法的收斂效能和穩態效能，在NSAF的基礎上結合全帶自適應濾波演算法的成比例理論，提出了幾種改進的NSAF演算法，例如不同形式的變步長因子NSAF以及變正則化引數NSAF。為了在識別稀疏回聲路徑時快速收斂，文獻[22,23]將NLMS演算法中的成比例思想以類比的方式融合到NSAF演算法中，提出了比例NASF（proportionate NASF，PNSAF）演算法和μ準則PNSAF（μ-law PNASF，MPNSAF）演算法。

因為子帶結構中存在混疊分量問題

Keermann於1988年利用取樣濾波器組技術消除了混疊現象，但是此舉增加了演算法複雜度。
相鄰子帶間留安全頻帶，缺點：引入了空白頻帶，降低了訊號質量。
重疊子濾波器補償法，缺點：因為交叉項而增加了運算量，還降低了收斂速度。

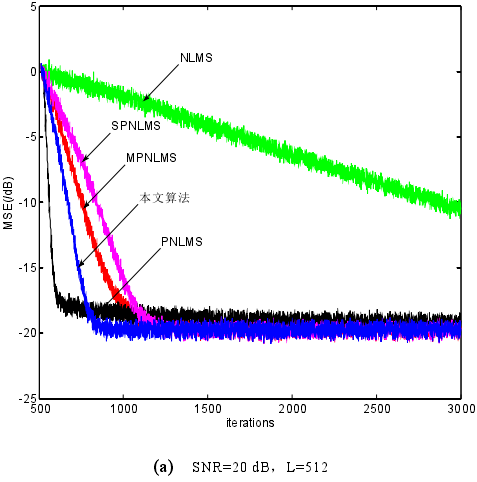
2004年K. A. Lee 和 W. S. Gan提出了基於最小擾動原理的多帶結構式自適應濾波器(Multiband Structured SAF，MSAF)演算法，並給出了自適應濾波器抽頭係數的更新方程。該結構完全不存在濾波器輸出端的混疊分量問題。

多帶自適應濾波器

　　子帶自適應濾波器中每個子帶單獨使用一個子濾波器。該結構會導致輸出端產生混疊分量，解決此問題的傳統方法多以降低訊號的質量或增大穩態誤差為代價，Lee 和 Gan在 2004 年提出了一種全新多帶結構。不同於子帶濾波器在每個子帶都使用不同的濾波器，多帶結構的每個子帶使用相同的全帶濾波器，這很好地克服了輸出端存在混疊分量的問題。

頻域自適應濾波

問題：針對回聲路徑很長且複雜，並且回升延遲較高時，時域自適應濾波演算法計算複雜度高的問題，

解決：[12~14]提出了==多延遲頻域分塊濾波==（MDF）演算法，MDF演算法將長度為L的自適應濾波器分成FFT長度
的整數倍個子塊，對輸入訊號的每個子塊進行頻域內的LMS演算法。

優點：當回聲路徑很長且複雜時計算量小，並且在**收斂速度**方面有略微提升。

綜上所述

《聲學回聲消除中子帶和塊稀疏自適應演算法研究_魏丹丹》

遠端輸入語音訊號的相關性較高，且聲學回聲通道的衝擊響應一般只有少量的非零係數，因此是一個稀疏通道。

針對用於聲學回聲消除的子帶和塊稀疏演算法進行了研究和改進，以達到提高演算法跟蹤效能和抗衝激魯棒性的目的。本文的主要貢獻如下：

首先，區別於傳統文獻中子帶歸一化自適應演算法消除回聲的方法，

我提出一種用於聲學回聲消除的新型子帶歸一化自適應濾波切換演算法(LMS-NSAF)。

該演算法核心思想是根據語音訊號的狀態不同，採用 VAD 快慢包絡技術切換演算法，當輸入遠端訊號的瞬時能量值較大時，使用收斂速度快的子帶 NLMS 演算法，當輸入訊號的瞬時能量值較小時，則使用計算複雜度低的權重向量更新公式，從而使得改進的子帶 NLMS 演算法在提高收斂性的同時又能降低演算法的計算複雜度

基於多帶結構的改進型自適應濾波切換演算法NLMS-NSAF

首先遠端語音訊號利用包絡法判別有無語音段，

然後將訊號狀態輸出到自適應多帶結構演算法模組當中。

若語音區輸入訊號的短時能量較大，則使用收斂速度快的自適應濾波演算法(NLMS)；

若語音區輸入訊號的短時能量較小，需考慮計算量低的演算法(NSAF)，

當然，語音在無語音區時演算法迭代停止。

對輸入語音訊號能量高低的判定是通過和閾值比較得到的。在充分考慮語音特性的情況下，切換演算法實現了演算法在收斂速度的優勢，同時完成了同演算法複雜度的優化選擇。最後達到了提高濾波演算法效能、降低運算量的目的。

有人說：基於維納濾波發展起來的 LMS 演算法因其結構簡單，運算量小，穩定性好等特性，依然是目前得到廣泛應用的一種自適應濾波演算法。

回聲路徑是經典的稀疏路徑，且語音訊號作為遠端輸入時相關性較強，

其中最典型最有代表性的兩類自適應演算法就是：最小均值誤差(LMS)演算法、遞推最小二乘(RLS)演算法。[參考]( https://blog.csdn.net/tianwenzhe00/article/details/88192783 )

參考

聲學回聲消除中子帶和塊稀疏自適應演算法研究_魏丹丹

《車載擴音系統降噪演算法的研究以及硬體實現》__張雪