CSAPP：程式碼優化【矩陣讀寫】

阿新 • • 發佈：2019-11-04

轉載請註明出處：https://www.cnblogs.com/ustca/p/11790314.html
寫程式最主要的目標就是使它在所有可能的情況下都正確工作，另一方面，在很多情況下，讓程式執行得很快也是一個重要的考慮因素。

編寫高效程式需要做到以下兩點：

選擇一組合適的演算法和資料結構
編寫編譯器能夠有效優化以轉換成高效可執行程式碼的原始碼

第一點合適的演算法和資料結構往往是大家寫程式時會首先考慮到的，而第二點常被忽略。這裡我們就程式碼優化而言，主要討論如何編寫能夠被編譯器有效優化的原始碼，其中理解優化編譯器的能力和侷限性是很重要的。

以下我們將舉例對常見的矩陣操作進行程式碼優化。

目標函式：影象逆時針旋轉90°

旋轉操作用下面兩步操作完成：

Transpose: 對第（i,j）個畫素，執行Mij和Mji交換
Exchange rows：行i和行N-1-i交換

原理圖：

即對原有影象矩陣先進行一次對摺，然後再進行一次翻轉，就可以得到我們需要的逆時針旋轉90°之後的矩陣。

其中我們用以下結構體表示一張影象的畫素點：

typedef struct { 
    unsigned short red;   /* R value */ 
    unsigned short green; /* G value */ 
    unsigned short blue;  /* B value */ 
} pixel;

red、green、blue分別表示一張彩色影象的紅綠藍三個通道。

原旋轉函式如下：

#define RIDX(i,j,n) ((i)*(n)+(j))

void naive_rotate(int dim, pixel *src, pixel *dst) { 
    int i, j; 
    for(i=0; i < dim; i++) 
        for(j=0; j < dim; j++) 
            dst[RIDX(dim-1-j,i,dim)] = src[RIDX(i,j,dim)]; 
    return;
}

影象是標準的正方形，用一維陣列表示，第（i,j）個畫素表示為I[RIDX(i,j,n)]，n為影象邊長。

引數：

dim：影象的邊長
src：指向原始影象陣列首地址
dst：指向目標影象陣列首地址

RIDX(i,j,dim)讀取目標畫素點，RIDX(dim-1-j,i,dim)將i、j引數位置互換，實現了斜角對摺，dim-1-j實現了上下翻轉。

優化目標：使旋轉操作執行的更快

當前我們擁有一個driver.c檔案，可以對原函式和我們優化的函式進行測試，得到表示程式執行效能的CPE（每元素週期數）引數。

我們的任務就是實現優化程式碼，與原有程式碼同時執行進行引數的對比，檢視程式碼優化情況。

優化的主要方法

迴圈展開
平行計算
提前計算
分塊運算
避免複雜運算
減少函式呼叫
提高Cache命中率

迴圈主體只存在一條語句，該語句為記憶體的讀寫（讀取一個源畫素，再寫入目標畫素），不涉及函式呼叫與計算。所以我們的優化手段有提高Cache命中率、避免複雜運算、分塊運算、迴圈展開與平行計算。

優化一：提高Cache命中率

在矩陣運算中，提高Cache命中率是最容易想到的方法，常見的是外迴圈按行遍歷與外迴圈按列遍歷的對比，因為儲存順序是行序，所以前者的執行速度會明顯優於後者。

在已給出的naive_rotate函式中，核心迴圈語句涉及到讀取一個畫素點與寫入一個畫素點，顯然寫入畫素點比讀取畫素點更耗費時間，這是由儲存器的性質決定的，所以我們應該優先對寫入畫素點的索引進行優化。

上圖描述了8種陣列索引順序，位於上方的藍色方塊代表原始影象，黃色箭頭表示原始畫素的讀取順序，位於下方的藍色方塊代表旋轉後圖像，紅色箭頭表示目標畫素的寫入順序。

由於迴圈體執行速度主要與資料寫入相關，所以我們優先考慮紅色箭頭也就是寫入畫素的cache命中率。

第一組到第四組的寫入畫素都是按照列序，理論上寫入效果應該最差，第五第六組正向行序寫入執行效果應該是最好的，第七第八組逆向行序應該稍差。下面我們給出分別按照8種不同順序索引的程式碼，使用driver測試出他們的執行效率：

void rotate_leftup(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (i = 0; i < dim; i++)
    for (j = 0; j < dim; j++)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_leftdown(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (i = dim-1; i > -1; i--)
    for (j = 0; j < dim; j++)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_rightup(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (i = 0; i < dim; i++)
    for (j = dim-1; j > -1; j--)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_rightdown(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (i = dim-1; i > -1; i--)
    for (j = dim-1; j > -1; j--)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_upleft(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (j = 0; j < dim; j++)
    for (i = 0; i < dim; i++)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_upright(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (j = dim-1; j > -1; j--)
    for (i = 0; i < dim; i++)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_downleft(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (j = 0; j < dim; j++)
    for (i = dim-1; i > -1; i--)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}
void rotate_downright(int dim, pixel *src, pixel *dst) 
{
    int i, j;
    for (j = dim-1; j > -1; j--)
    for (i = dim-1; i > -1; i--)
        dst[RIDX(dim-1-j, i, dim)] = src[RIDX(i, j, dim)];
}

CPE與機器執行速度有關，測試機比較老，又是虛擬機器環境，所以測得的CPE很低

Dim：影象大小
Your CPEs：對應函式CPE
Baseline CPEs：參考基線CPE
Speedup：加速比 = Baseline CPEs / Your CPEs

與理論估計的一樣，前4組表現明顯最差，其中的第一組正是原始待優化的函式，與理論估計相符。

第5-8組差異不大，第五第六組比第七第八組效果略好，但總體優化效果很不明顯，重新檢查迴圈體的執行語句，發現在索引時巨集定義中包含了乘法運算，嚴重阻礙了程式的執行效率。

優化二：避免複雜運算

之前在索引畫素點時，是通過乘法運算進行索引，加大了不必要的開銷。如果使用矩陣的分塊運算，雖然能夠利用區域性性原理在一定程度上優化程式，但依舊會受到乘法運算的嚴重影響，於是我們打算避免複雜運算通過迴圈展開的方式來對程式進一步優化。

具體的操作邏輯是，使用指標對元素進行索引，可以把之前的8種影象索引中的箭頭，分拆成32個平行的箭頭，通過指標運算一次處理32個畫素，下面給出程式碼來更好的理解：

//1
void rotate_pleftup(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(i=0;i<dim;i+=32)
        for(j=0;j<dim;j++){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = -1;
            while(++step < 32){
                *(dptr++) = *sptr;
                sptr += dim;
            }
        }
}
//2
void rotate_pleftdown(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(i=dim-1;i>30;i-=32)
        for(j=0;j<dim;j++){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = 1;
            while(--step > -32){
                *(dptr--) = *sptr;
                sptr -= dim;
            }
        }
}
//3
void rotate_prightup(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(i=0;i<dim;i+=32)
        for(j=dim-1;j>-1;j--){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = -1;
            while(++step < 32){
                *(dptr++) = *sptr;
                sptr += dim;
            }
        }
}
//4
void rotate_prightdown(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(i=dim-1;i>30;i-=32)
        for(j=dim-1;j>-1;j--){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = 1;
            while(--step > -32){
                *(dptr--) = *sptr;
                sptr -= dim;
            }
        }
}
//5
void rotate_pupleft(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(j=0;j<dim;j+=32)
        for(i=0;i<dim;i++){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = -1;
            while(++step < 32){
                *dptr = *(sptr++);
                dptr -= dim;
            }
        }
}//6
void rotate_pupright(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(j=dim-1;j>30;j-=32)
        for(i=0;i<dim;i++){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = -1;
            while(++step < 32){
                *dptr = *(sptr--);
                dptr += dim;
            }
        }
}
//7
void rotate_pdownleft(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(j = 0; j < dim; j+=32)
        for(i = dim-1; i > -1; i--){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = -1;
            while(++step < 32){
                *dptr = *(sptr++);
                dptr -= dim;
            }
        }
}
//8
void rotate_pdownright(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(j = dim-1; j > 30; j -= 32)
        for(i = dim-1; i > -1; i--){       
            pixel *dptr=dst+RIDX(dim-1-j,i,dim);
            pixel *sptr=src+RIDX(i,j,dim);
            int step = -1;
            while(++step < 32){
                *dptr = *(sptr--);
                dptr += dim;
            }
        }
}

指標每迴圈找到一個畫素，會對其所在的某一行或某一列的32個畫素進行變換，這樣既通過區域性性提高了cache命中率，也能夠有效的避開乘法運算造成的效能損失。以下是對優化一中的8個函式進行迴圈展開的優化情況：

可以看到，1、3的執行效果最好，2、4的執行效果相對略低，5-8執行效果最差，但即便是按照最差的順序迴圈展開，也遠遠超過了優化一中最好的索引順序，這也證明了乘法運算是阻礙之前優化的主要因素。

優化二中為什麼變成了1、3執行效率最好？

通過之前的8種迴圈次序的分析圖，我們可以看到1、3兩組在寫入的時候，如果使用32路迴圈展開，每次都可以通過指標索引到後面31個畫素（黑色箭頭代表其餘31路的寫入），cache命中率最高：

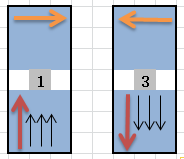
優化三：平行計算

優化二中的迴圈展開，其實也可以看作是一種特殊的分塊運算，分塊大小為1*32的小矩陣，各種優化方法之間總體來說具有相關性，大多都是基於cache快取考慮。

優化三中我們提高迴圈主語句執行的並行性，這裡我們需要在32路迴圈時加入一個新的指標，在巨集觀上來看迴圈主體每條語句是無法並行的，但每一行程式碼並不是一個原子操作，微觀到執行緒級別來看是可以出現並行的，這裡我們只對優化二中最好的第一組進行修改：

void rotate_pleftup_4(int dim, pixel *src, pixel *dst) 
{
    int i,j;
    for(i=0;i<dim;i+=32)
        for(j=0;j<dim;j++)
        {       
            pixel* dptr=dst+RIDX(dim-1-j,i,dim);
            pixel* sptr=src+RIDX(i,j,dim);

            pixel* dptr_ = dptr+1;
            pixel* sptr_ = sptr+dim;
            
            int step = -1;
            while(++step < 16){
                *dptr = *sptr;
                sptr += dim+dim;
                dptr += 2;
            
                *dptr_ = *sptr_;
                sptr_ += dim+dim;
                dptr_ += 2;
            }
        }
}

測試結果如下：

多次執行的話，得到的測試結果基本沒有效能差距，但是如果將迴圈指標繼續增加，使用4指標或者8指標迴圈，反而會出現效能下降的情況。

重新對原函式進行分析，函式主要執行的只是畫素點的讀寫而已，並且我們已經去掉了耗時的乘法運算。這樣一來，沒什麼能並行運算的地方，程式碼的並行性實際上並沒有什麼提升的空間，反而會隨著多個指標的加入使得迴圈過程變得複雜增大開銷，甚至可能會降低程式編譯時的效率。

另外，在沒什麼效能提升的情況下，採用多個指標變數使得程式碼可讀性變差，所以這裡我們選擇優化二的版本。

這並不意味著提高並行性的方法不好，只是在當前環境下不適用而已，如果使用得當會在原有基礎上給程式帶來更好的效能提升。

下面對比一下優化前和優化後的程式碼：

多出了5行迴圈語句，但加速比卻從1.2到了7.8，提升了6.5倍，不採用並行優化的情況下程式碼可讀性也未下降，這顯然是值得的。

我們經常會涉及到關於矩陣的處理，特別是影象處理方面，而影象處理對效能有很高的需求。這只是一個矩陣操作/二維陣列的簡單例子，程式碼優化不侷限於此，我們平時編碼中很多時候並沒有考慮那麼多，都是按照常規寫法逐步實現，這並沒有什麼不妥。但是當開始對自己的程式有提升效能的需求時，嘗試對自己的程式碼做出優化不妨是一種更好的選擇，這是寫出高質量程式碼的必要途徑

CSAPP：程式碼優化【矩陣讀寫】

目標函式：影象逆時針旋轉90°

優化目標：使旋轉操作執行的更快

優化的主要方法

優化一：提高Cache命中率

優化二：避免複雜運算

優化三：平行計算

CSAPP：程式碼優化【矩陣讀寫】

CSAPP：程式碼優化【矩陣運算】

CSAPP：逆向工程【緩衝區溢位攻擊】

微贊微擎V0.8以上版本：【資料庫讀寫分離】實戰教程 [複製連結]

鎖的優化 ReentrantReadWriteLock（讀寫鎖）資料共享通道：BlockingQueue

【黑金原創教程】【FPGA那些事兒-驅動篇I 】實驗十九：SDRAM模組② — 多字讀寫

【python coding 2：檔案讀寫】讀取本地檔案裡的ip地址，迴圈寫入到新的檔案中

2017 ACM/ICPC Asia Regional Shenyang Online：number number number hdu 6198【矩陣快速冪】

hadoop學習筆記（三）：hdfs體系結構和讀寫流程（轉）

java基礎學習總結（十六）：程式碼優化

Python：檔案批量建立、讀寫、複製、內容修改和重新命名

《深入應用C++11：程式碼優化與工程級應用》勘誤表

Go基礎系列：互斥鎖Mutex和讀寫鎖RWMutex用法詳述

【NTFS磁碟讀寫】Paragon NTFS for Mac 破解版中文破解版

教程：使用Data Lake Analytics讀/寫MongoDB資料

JS：對txt檔案進行讀寫，替換和新增

Tensorflow學習筆記：讀取二進位制檔案、讀寫TFRecord檔案

MySQL 對於千萬級的大表要怎麼優化？（讀寫分離、水平拆分、垂直拆分）

使用STM32CUBEMX生成USB Mass Storage程式碼，通過SDIO讀寫TF卡

Python練習【6】【數據庫操作 | 文件讀寫】

CSAPP：程式碼優化【矩陣讀寫】

目標函式：影象逆時針旋轉90°

優化目標：使旋轉操作執行的更快

優化的主要方法

優化一：提高Cache命中率

優化二：避免複雜運算

優化三：平行計算

相關推薦