概率

隨機變數：實驗的結果稱為隨機變數。
隨機變數分為：

• 離散隨機變數：如骰子。
• 連續隨機變數：如時間範圍。實數範圍（包含有理數和無理數）

因為隨機變數可以取不同的值，所以產出了概率分佈的概念，統計學家用概率分佈描述不同隨機變數發生的概率。因此有：

• 離散型概率分佈
• 連續型概率分佈

期望和均值

如果我們擲了無數次的骰子，然後將其中的點數進行相加，然後除以他們擲骰子的次數得到均值，這個有無數次樣本得出的均值就趨向於期望。

均值是針對樣本發生的頻率而言的，期望是針對樣本發生的概率分佈而言的，所以總結後便是：
概率是頻率隨樣本趨於無窮的極限。
期望是均值隨樣本趨於無窮的極限。
上述表達的意思其實也就是弱大數定理

對於期望的理解：
理解1:
期望是反應樣本平均值的指標，但是個體資訊被壓縮，所以看一個期望值的指標，需要採用“期望+數量”組合的方式去調研。

理解2:
平均數是根據實際結果統計得到的隨機變數樣本計算出來的算術平均值，和實驗本身有關，而數學期望是完全由隨機變數的概率分佈所確定的，和實驗本身無關。

實驗的多少是可以改變平均數的，而在你的分佈不變的情況下，期望是不變的。

期望（均值）、方差、標準差

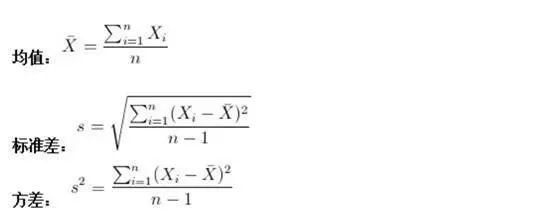
方差：在概率論和數理統計中,方差（英文Variance）用來度量隨機變數和其數學期望（即均值）之間的偏離程度.方差越大，隨機變數的結果越不穩定。常用來評估風險。
標準差：概念和方差一樣，都是表示樣本的離散程度。

標準差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準差，代表一組資料裡大部分的數值和其平均值之間差異較大；一個較小的標準差，代表這些數值較接近平均值。（eg：兩組數的集合 {1, 4, 9, 14} 和 {5, 6, 8, 9} 其平均值都是7，但第二個集合裡的數字明顯與7距離“更近”，通過公式算出第一個集合的標準差約為4.9，第二個約為1.5。）

為什麼引入標準差？
因為在實踐中，我們發現相當多的資料都呈現近似於“正態分佈”。在正態分佈圖中，均值可以告訴我們中間的峰值是多少，而標準差則決定了寬度。

反過來正態分佈也可以用來解釋標準差：在一個標準正態分佈中，數字出現的概率是固定的。

在方差和標準差之間如何選擇？
方差只是計算標準差過程中產生的一箇中間值，但是大多數情況下並不需要此中間值，而是採用了標準差，原因如下：
（1）表示離散程度的數字與樣本資料點的數量級一致，更適合對資料樣本形成感性認知。依然以上述10個點的CPU使用率資料為例，其方差約為41，而標準差則為6.4；兩者相比較，標準差更適合人理解。
（2）表示離散程度的數字單位與樣本資料的單位一致，更方便做後續的分析運算。
（3）在樣本資料大致符合正態分佈的情況下，標準差具有方便估算的特性：66.7%的資料點落在平均值前後1個標準差的範圍內、95%的資料點落在平均值前後2個標準差的範圍內，而99%的資料點將會落在平均值前後3個標準差的範圍