資料庫關係理論模式分解理解和總結
阿新 • • 發佈:2019-11-30
Armstrong公理系統
邏輯蘊涵
定義/解釋
比如A->B B->C 在關係模型R<U,F>中成立,可以得到A->C字R中也成立,所以稱F邏輯蘊含A->C。
閉包
定義/解釋
在關係模型R中,F所邏輯蘊涵的所有函式依賴叫做F的閉包,記為\(F^{+}\)。
某個屬性集關於依賴集的閉包
定義/解釋
即已有X這個屬性集作為左部,通過依賴集F的所有函式依賴,可以推匯出的所有函式依賴,稱為X關於F的閉包,記為\(X_F^{+}\)
例題
已知關係模型R<U,F>,其中U={A,B,C,D,E} F={AB->C,B->D,C->E,EC->B,AC->B},求\((AB)_F^{+}\)。
演算法:把AB作為左部,然後從F中找到左部是完全屬於AB的,把對應的右部併到AB裡,作為新的左部,重複直到不能再增加左部或者已經等於全集。
結果:\((AB)_F^{+}\)=ABCDE
最小依賴集
例題
F={abd->e,ab->g,b->f,c->j,cj->i,g->h}
演算法:
- 將右部有多個的拆開,比如ab->cd 變成 ab->c,ab->d
- 嘗試刪除左側的冗餘函式依賴,具體操作是對於每個函式依賴X->A,假設將該依賴刪除,然後求X在剩下的依賴集中的閉包\(X_G^{+}\),如果A屬於這個閉包,那麼就可以刪除。
- 嘗試刪除左側的冗餘屬性,具體操作是對於剩下的每個有多個屬性的函式依賴X->A,對於每個屬性,假設將該屬性刪除,然後求剩下的屬性集在F中的閉包\((X-B_i)^{+}_F\),如果A屬於這個閉包,則可以刪除。
結果:F={abd->e,ab->g,b->f,c->j,c->i,g->h}
求候選碼
例題
已知關係模型R<U,F>,其中U=(A,B,C,D,E,G),F={AB-->C,CD-->E,E-->A.A-->G},求R的候選碼。
演算法:
- 找出只在函式依賴左部出現的屬性集X,X肯定是任意一個候選碼的成員,因為只在左邊出現,所以少了它肯定推不出全集U。
- 只在右部出現,肯定不屬於任何一個候選碼。
- 其他的情況嘗試組合求閉包,如果閉包是全集U,那麼就是候選碼。
結果:
只在左邊出現的是B和D,所以確定了BD,只在右邊出現的是G,所以排除G,剩下A,C,E。
先考慮一個的組合,ABD,BCD和BDE,三個的閉包都是全集U,所以三個都是候選碼,演算法結束。
模式分解
判斷是否無損連線
演算法
- 對於一個分解,有k個子集,n個屬性,建立一張k行n列的初始表,對於每一行也就是分解的每個子集,把該分解子集出現的屬性對應的列寫上\(a_j\),否則寫上\(b_{ij}\)
- 對於每一個依賴,找到左部屬性對應的列,根據行的值分組,對於行的值相同的這些行,檢視對應右部屬性的列,如果這些格子裡有a值,那把所有這些格子改成a值,如果沒有,改成行最小的b值。如果某個b值改成a值,那麼其他行(不屬於當前操作的行)的相同b值也要改成a值。
- 如果不變則停止,如果出現有一行為a1 a2 ... an,那麼說明該連線為無損連線。
例題
參考
已知R<U,F>,U={A,B,C,D,E},F={A→C,B→C,C→D,DE→C,CE→A},R的一個分解為R1(AD),R2(AB),R3(BE),R4(CDE),R5(AE),判斷這個分解是否具有無損連線性。
- 根據每個分解的屬性,構造出初始表
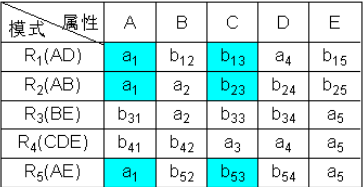
- 然後看第一個依賴A->C,找到A對應的第一列,其中1 2 5行的值相等,找到C對應的第三列,對應格子沒有a值,所以全部改成\(b_{13}\)。
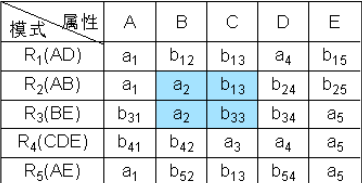
- 同理看第二個依賴,B->C,把\(b_{33}\)改成\(b_{13}\)。
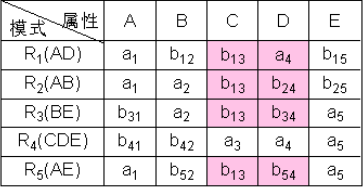
- 以此類推

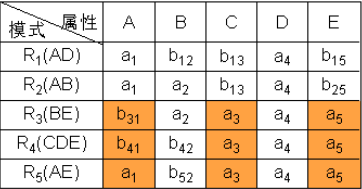
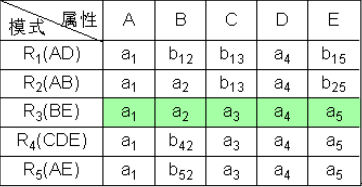
- 最後第三行有a1 a2 a3 a4 a5,所以該分解具有無損連線性。
3NF和保持函式依賴的分解
演算法
- F=F的最小依賴集
- \(U_0\)={不在F出現的屬性}
- U=U-\(U_0\)
- 若F中有函式依賴X->A,使得XA=U,那麼分解就是R本身
- 如果沒有,將剩下的F按左部分組,得到\(U_i\),分解就是{\(R_1\)<\(U_1\),\(F_1\)>,...} ∪ \(R_0\)<\(U_0\),\(F_0\)>
3NF和保持函式依賴和具有無損連線性的分解
演算法
- 求出3NF和保持函式依賴的分解。
- X是R的碼,讓已有的分解∪上一個{\(R^{*}\)<X,\(F_X\)>}。
- 如果分解中有某個\(U_i\)屬於X,那麼刪掉該\(U_i\),如果X屬於某個\(U_i\),那麼刪掉。
BCNF和具有無損連線性的分解
演算法
- 類似遞迴的方法,首先判斷自身是不是BC正規化,如果是,無需分解。
- 否則,找到當前關係R的主碼,找到一個左邊不含主碼的依賴X->A,設U1=A,分解出去,剩下的U2=U-{A}作為一個關係模式,繼續重複上面的步驟。
- 根據X->A的選擇的不同,得到的分解也是不同。
4NF和具有無損連線性的分解
演算法
- 求出BCNF和具有無損連線性的分解。
- 對於一個關係R<U,F>,如果多值依賴X-->Y成立,則分解{R1<X,Y>,R2<X,Z>)}具有無損連線性,其中Z=U-X-Y。
