紅黑樹的插入和刪除
要想知道什麼是紅黑樹,首先要了解什麼是二叉查詢樹。
什麼是二叉查詢樹?
二叉查詢樹的特性:
1)左子樹上所有節點的值均小於或等於它的根節點的值
2)右子樹上所有節點的值均大於或等於它的根節點的值
3)左右子樹也一定為二叉排序樹
下面就是一顆標準的二叉查詢樹:
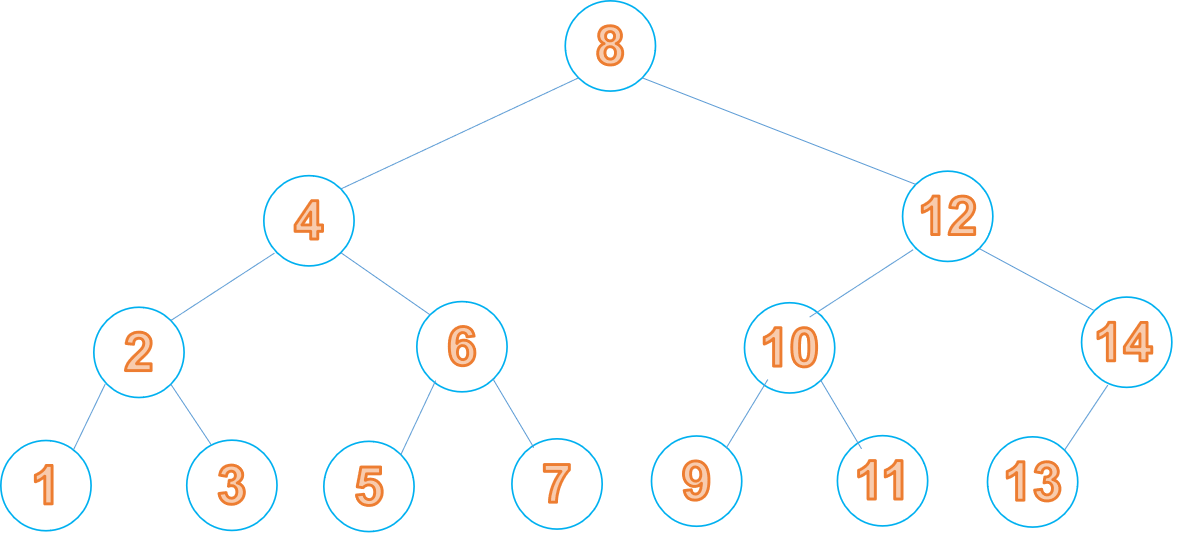
我們在向二叉查詢樹中進行增加或刪除節點的操作時,會出現樹的傾斜情況,比如下面的情況:
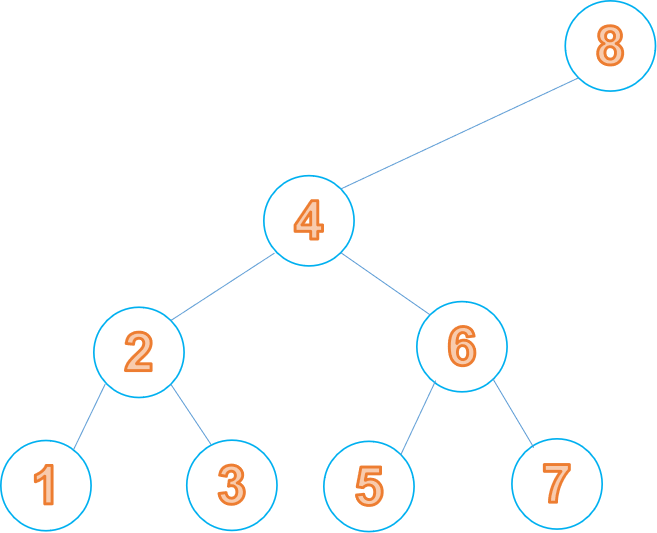
為了解決這個問題,產生了紅黑樹。
什麼是紅黑樹?
紅黑樹的特性:
1)節點是紅色或者黑色
2)根節點是黑色
3)每個葉子節點都是黑色的空節點
4)每個紅色節點的兩個子節點都是黑色的
5)從任意節點到其每個葉子的所有路徑都包含相同的黑色節點
只要滿足這五個特性,就是一顆紅黑樹,紅黑樹的平衡操作,也是針對這五個特性來做的。下面介紹一下紅黑樹是怎麼進行插入以及刪除操作的。
紅黑樹的插入:
我們假設紅黑樹當前的狀態如下圖所示
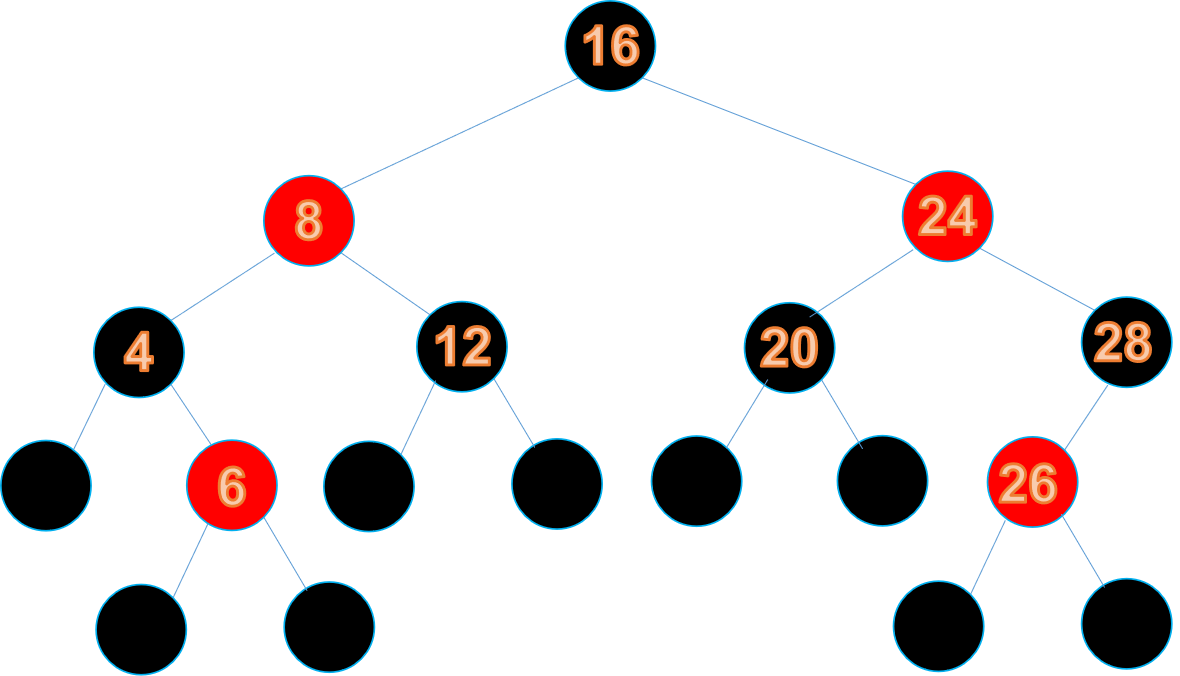
我們向其中插入節點25,插入之後如下所示:

為了滿足特性五,節點25的初始狀態必須是紅色節點,但是我們發現它的父節點26也是紅色節點,打破了特性4:每個紅色節點的兩個子節點都是黑色的,此時紅黑樹需要作出調整
調整方式:
1)變色
由於26不滿足特性4,所以將26變為黑節點
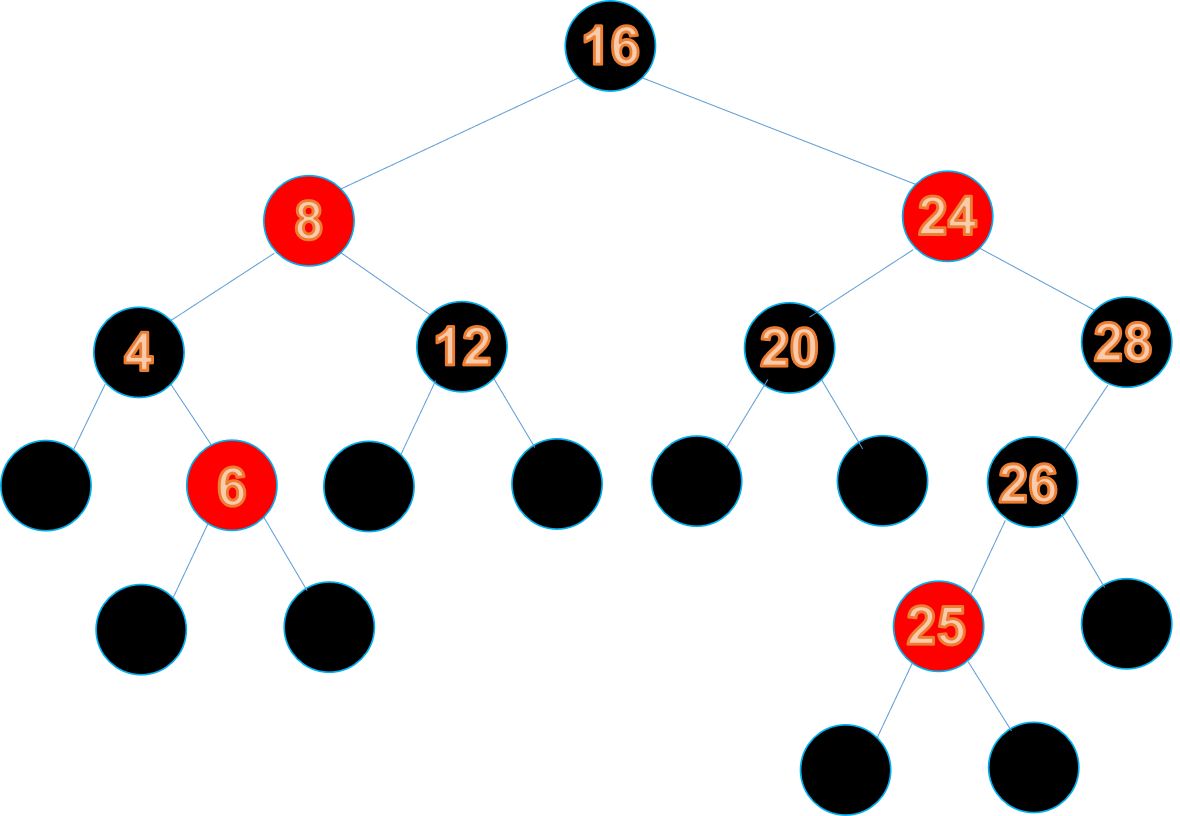
這樣又違背了特性5,所以把28變為紅節點
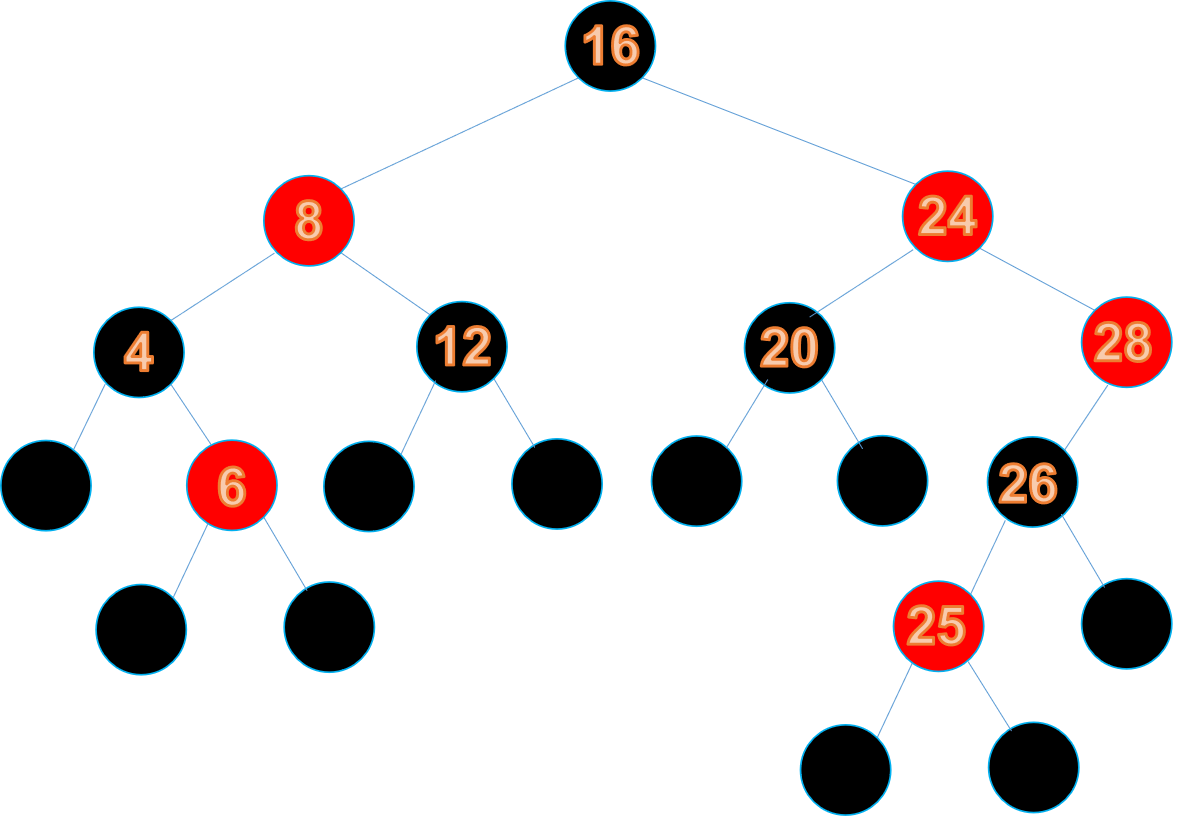
此時,如果繼續將節點24變為黑色,那麼節點16將無法變換,所以根節點需要進行左旋轉(24作為根節點,它的父節點作為它的左子樹,它的左子樹作為父節點的右子樹)
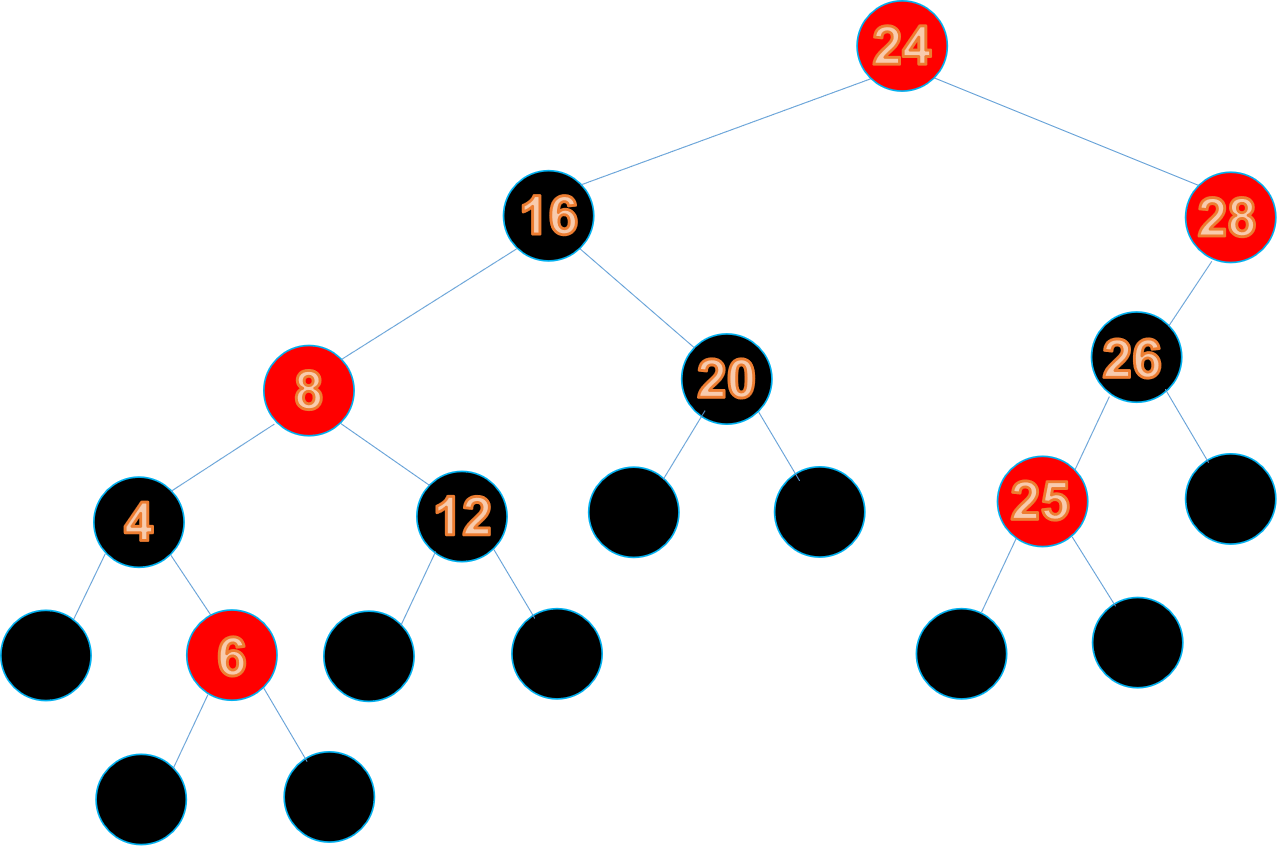
此時不滿足特性2,根節點必須為黑色,所以將根節點變為黑色
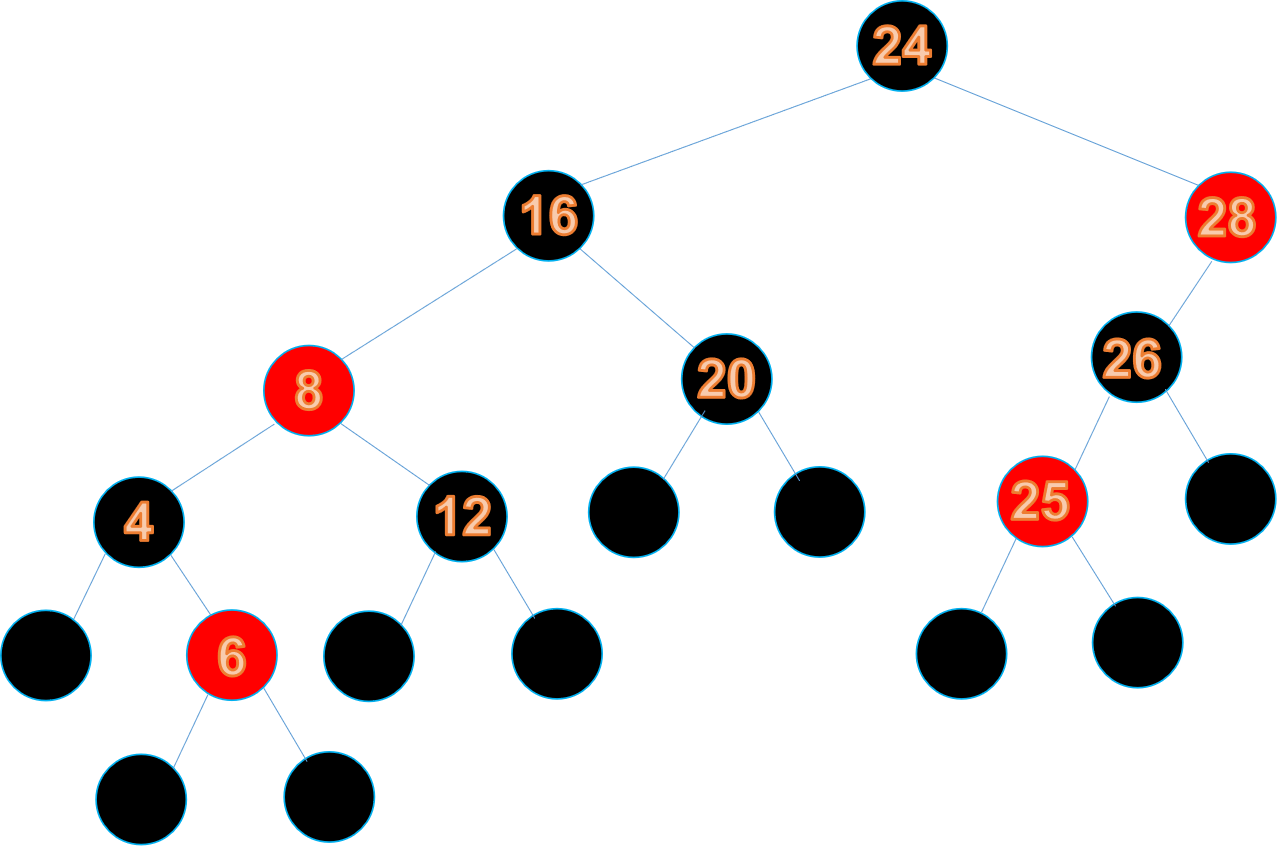
此時以節點16為根的子樹不滿足特性5,所以將節點16進行右旋轉
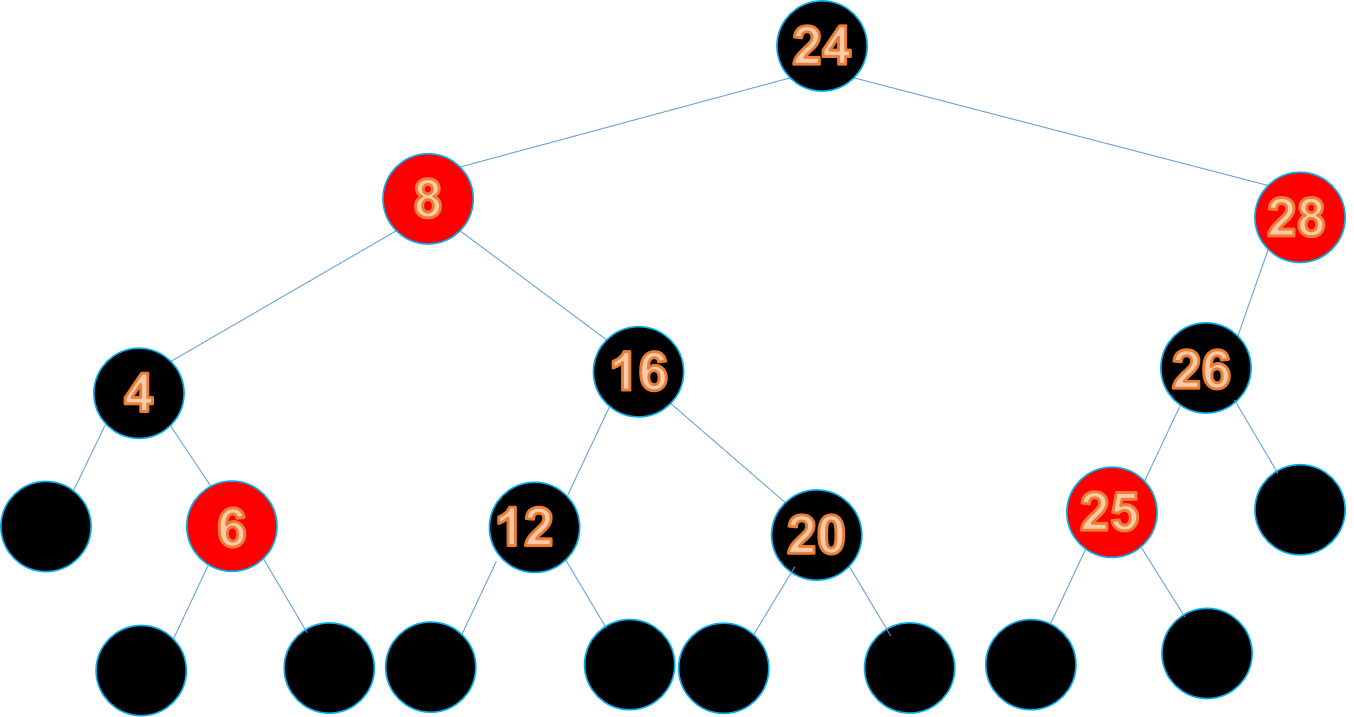
根據規則,將節點12和20變為紅節點
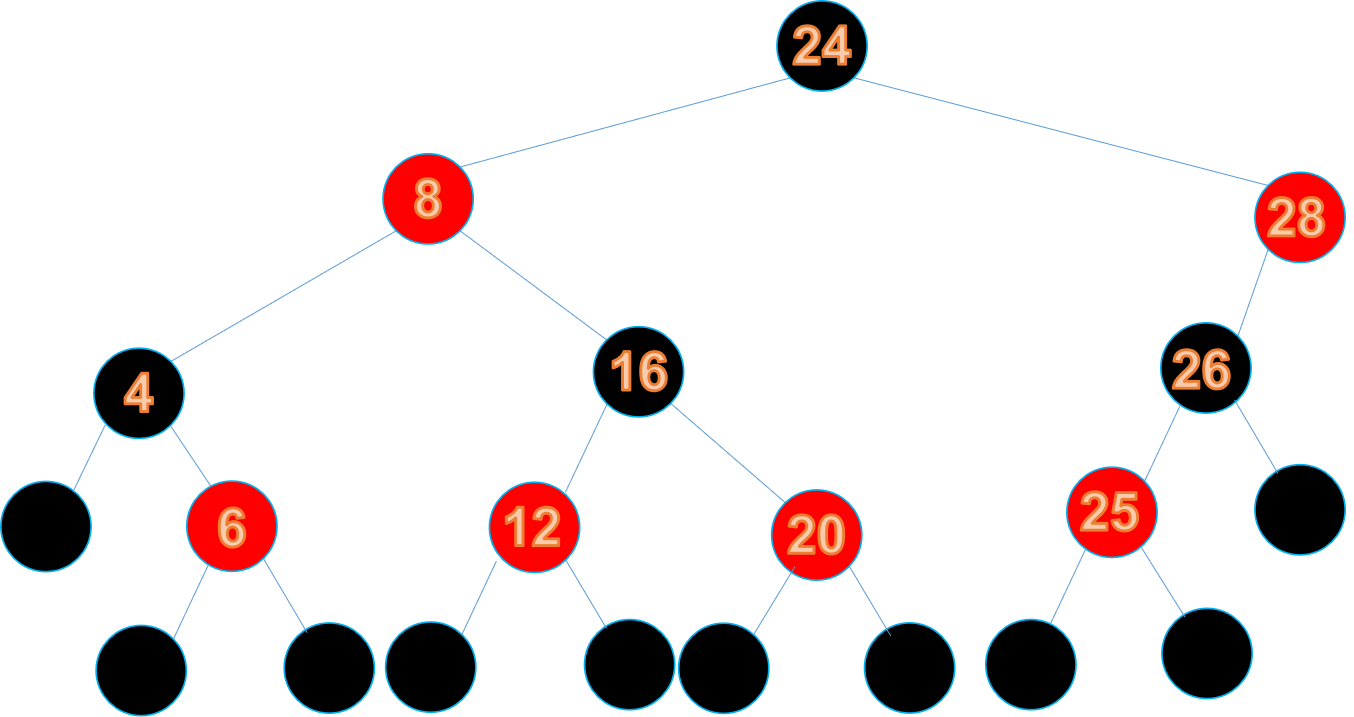
調整結束
由此我們就會發現,紅黑樹的五個特性互相制約,確保了紅黑樹中除葉子節點外,相同顏色的兩個節點不會相連,進而保證了不會出現某條路徑比其他路徑長出兩倍的情況
在對紅黑樹進行平衡的過程中,要儘量進行變色操作,一旦發現變色解決不了問題了,才會對其進行旋轉
紅黑樹的刪除:
想要對紅黑樹進行刪除操作,首先要把它當做一顆二叉查詢樹,對二叉查詢樹進行節點的刪除,然後再對其做平衡調整
二叉查詢樹節點的刪除主要有以下幾種情況:
1)待刪除的節點無左右孩子
此時只需要將該節點直接刪除就好
2)帶刪除的節點只有左孩子或者右孩子
3)待刪除的節點既有左孩子又有右孩子
首先需要找出它的右子樹的最左孩子,換句話來說就是右子樹中最小的節點,然後將該節點與待刪除的節點進行互換,最後將該節點刪除,因為是交換的節點是它右子樹的最左孩子,所以該節點只會有兩種情況
1)該節點無左右孩子,此時對應情況1
2)該節點有右孩子,此時對應情況2
根據具體的情況,進行對應的操作就好了
這樣,我們就完成了節點的刪除,下面需要對紅黑樹進行平衡了
我們看下面這張圖:

假如我們要刪除節點26,我們可以看到滿足情況1,該節點無左右孩子,所以我們可以直接把節點26刪除,刪除之後就是下面這個樣子:
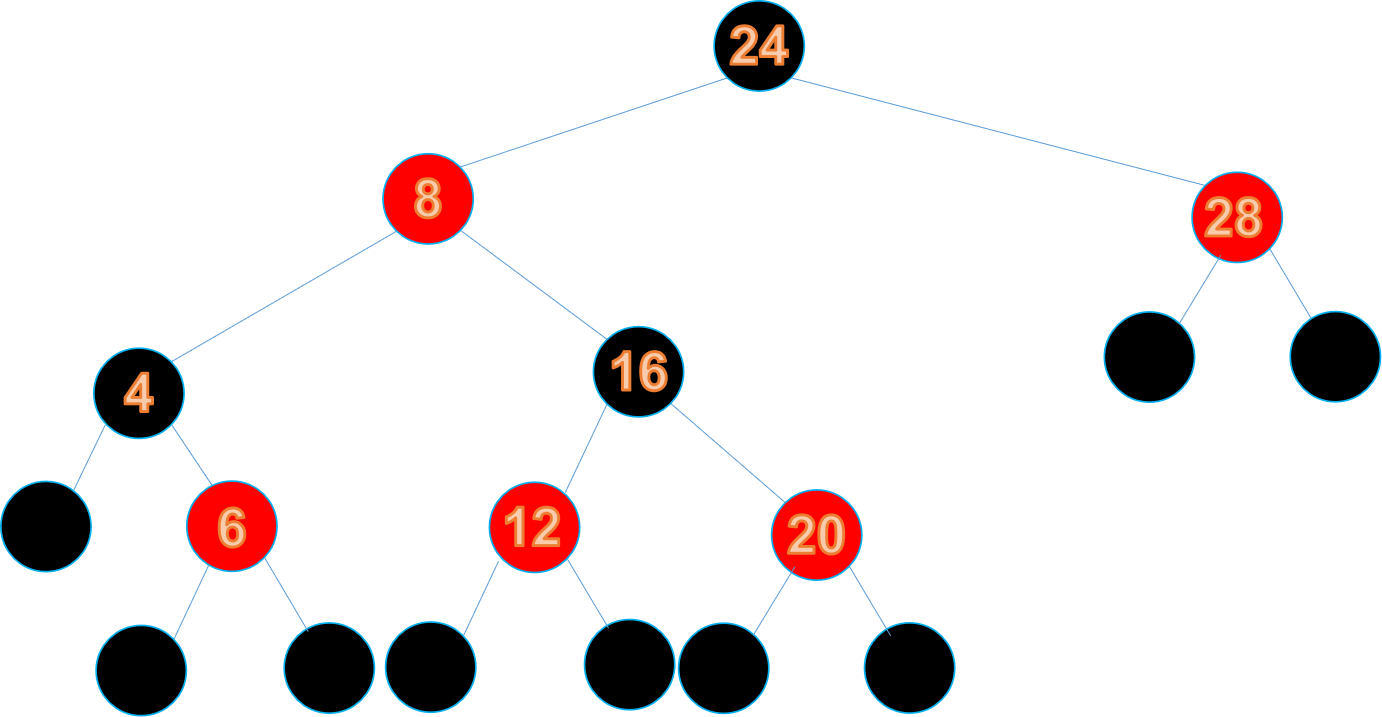
此時,我們發現從根節點開始遍歷,遍歷到左節點所經過的黑色節點數與遍歷到有右節點所經過的黑色節點數不同,此時需要對其進行平衡。若要使其滿足特性五,我們發現無法通過簡單的變色操作進行平衡,所以需要對其進行右旋,旋轉之後的紅黑數就是下面這個樣子
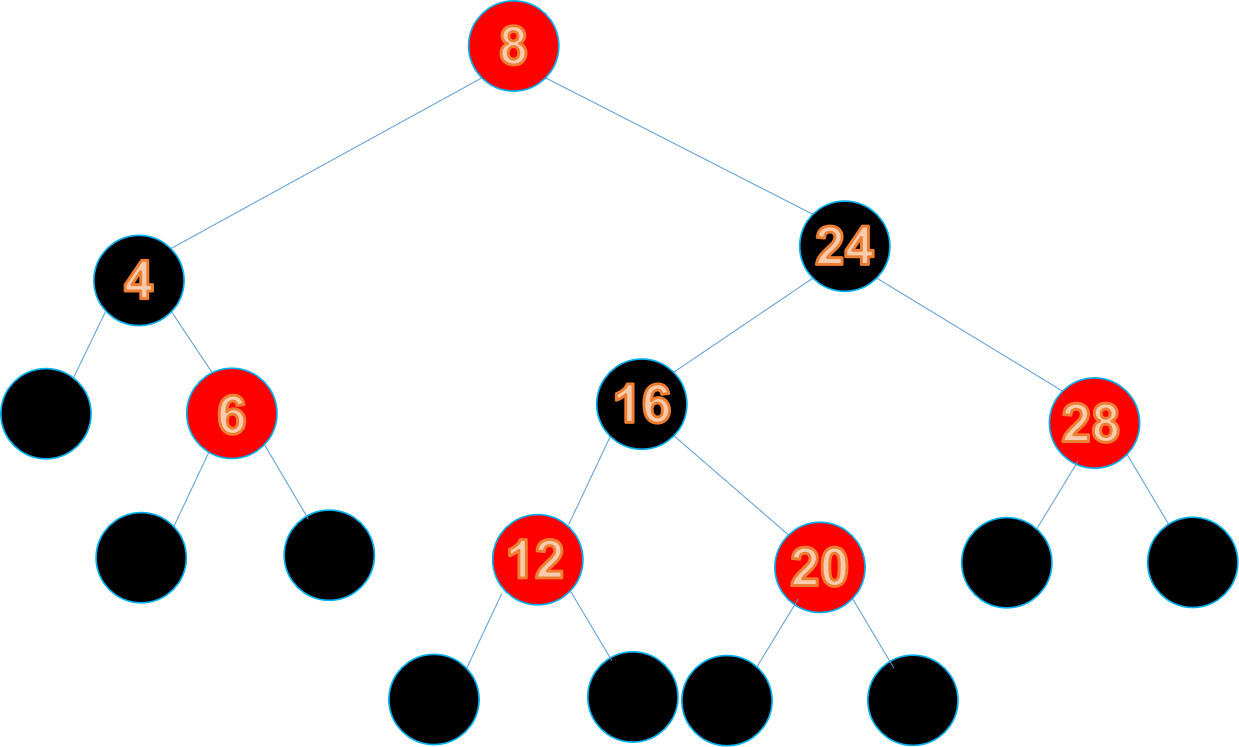
然後為了滿足條件1,我們把根節點變為黑色
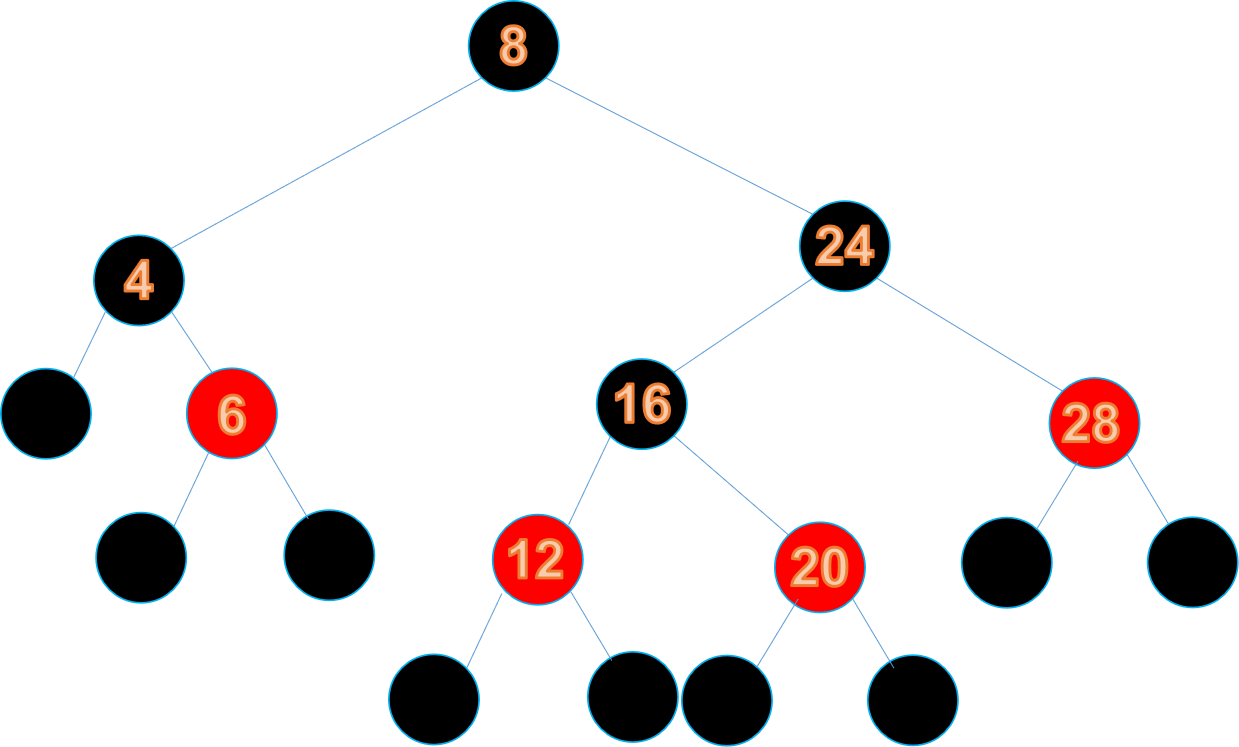
然後我們發現遍歷右子樹的葉子節點經過的黑色節點數要多於左子樹,所以將節點24變為紅色,再把節點28變為黑色:

這樣就完成了紅黑樹的刪除操作啦
