引言：

    目前國內圖書市場上，抑或網上講解紅黑樹的資料層次不齊，混亂不清，沒有一個完整而統一的闡述。而本人的紅黑樹系列四篇文章（詳見文末的參考文獻），雖然從頭至尾，講的有根有據，層次清晰，然距離讀者真正做到紅黑樹瞭然於胸，則還缺點什麼。

    而我們知道，即便在經典的演算法導論一書上，也沒有把所有的插入、刪除情況一一道盡，直接導致了不少讀者的迷惑，而我的紅黑樹系列第4篇文章：一步一圖一程式碼，一定要讓你真正徹底明白紅黑樹，雖然早已把所有的插入、刪除情況都一一道盡了，但也缺了點東西。

    缺點什麼東西列?對了，缺的就是一個完完整整的，包含所有插入、刪除情況全部過程的全程演示圖，即缺一個例子，缺一個完整的圖來從頭至尾闡述這一切。

    ok，本文，即以40幅圖來全程演示此紅黑樹的所有插入，和刪除情況。相信，一定會對您理解紅黑樹有所幫助。

    話不絮煩，下面，本文便以此篇文章：一步一圖一程式碼，一定要讓你真正徹底明白紅黑樹為綱，從插入一個結點到最後插入全部結點，再到後來一個一個把結點全部刪除的情況一一闡述。

    由於為了有個完整統一，紅黑樹插入和刪除情況在此合作成一篇文章。同時，由於本人的紅黑樹系列的四篇文章已經把紅黑樹的插入、刪除情況都一一詳盡的闡述過了，因此，有關紅黑樹的原理，本文不再贅述，只側重於用圖來一一全程演示結點的插入和刪除情況。有任何問題，歡迎指正。

紅黑樹插入情況全過程演示

       通過本人的紅黑樹系列第4篇文章，我們已經知道，紅黑樹的所有插入情況有以下五種：

情形1: 新節點N位於樹的根上，沒有父節點
情形2: 新節點的父節點P是黑色
情形3:父節點P、叔叔節點U，都為紅色，
[對應第二篇文章中，的情況1：z的叔叔是紅色的。]
情形4: 父節點P是紅色，叔叔節點U是黑色或NIL; 
插入節點N是其父節點P的右孩子，而父節點P又是其父節點的左孩子。
[對應我第二篇文章中，的情況2：z的叔叔是黑色的，且z是右孩子]
情形5: 父節點P是紅色，而叔父節點U 是黑色或NIL，
要插入的節點N 是其父節點的左孩子，而父節點P又是其父G的左孩子。
[對應我第二篇文章中，情況3：z的叔叔是黑色的，且z是左孩子。]

首先，各個結點插入與以上的各種插入情況，一一對應起來，如圖：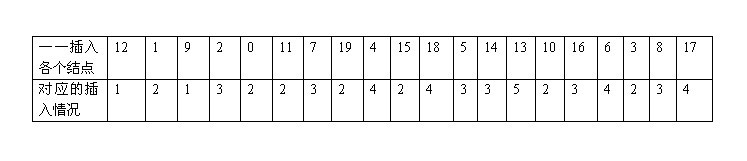

    以下的20張圖，是依次插入這些結點：12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示圖，已經把所有的5種插入情況，都全部涉及到了：

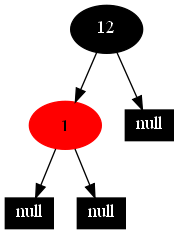
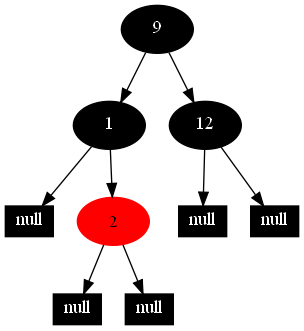
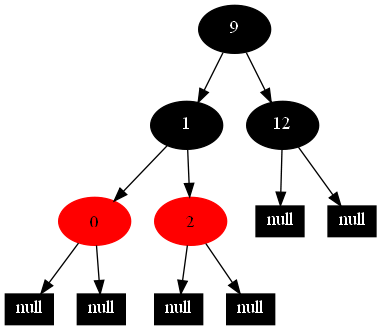
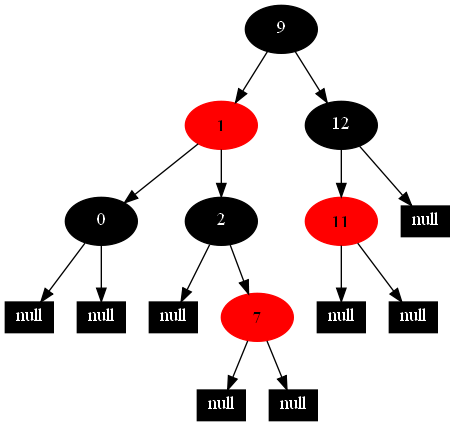
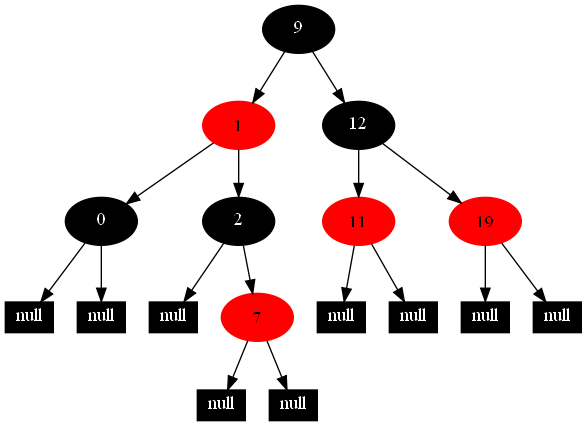
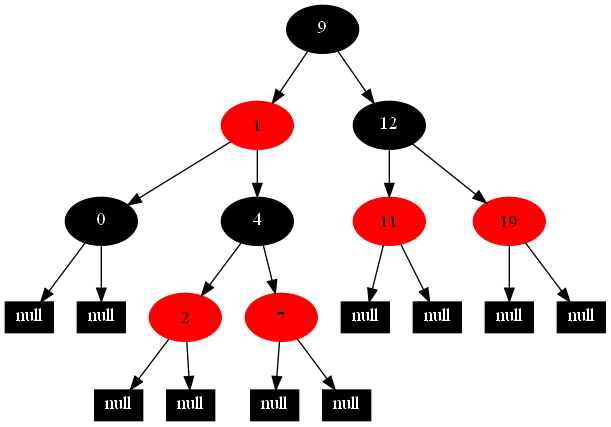
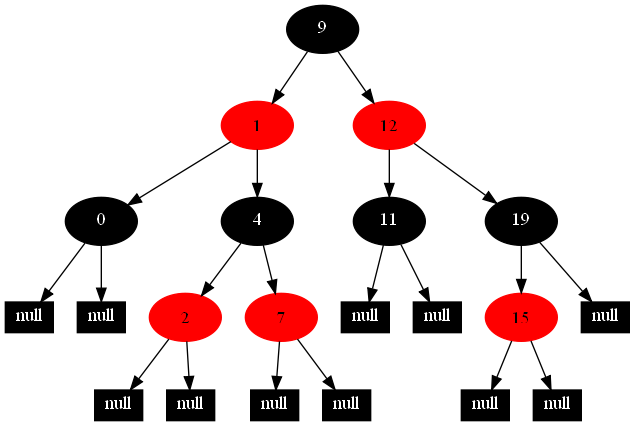
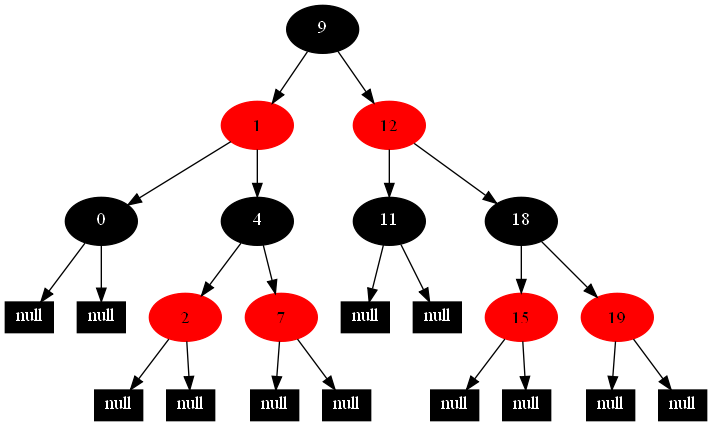
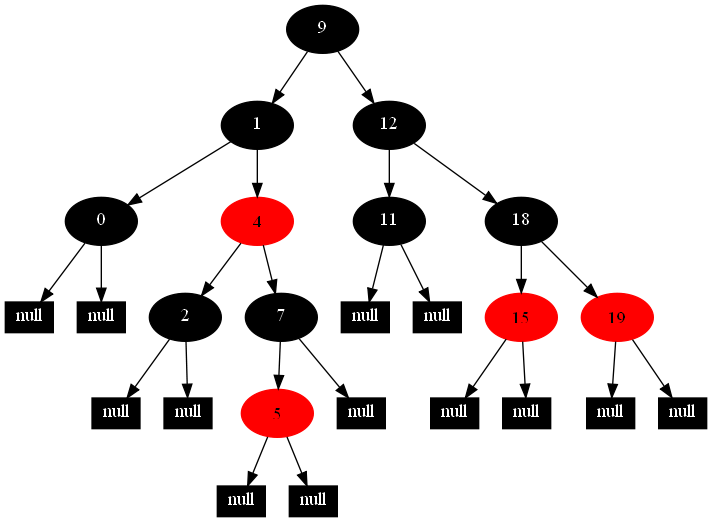
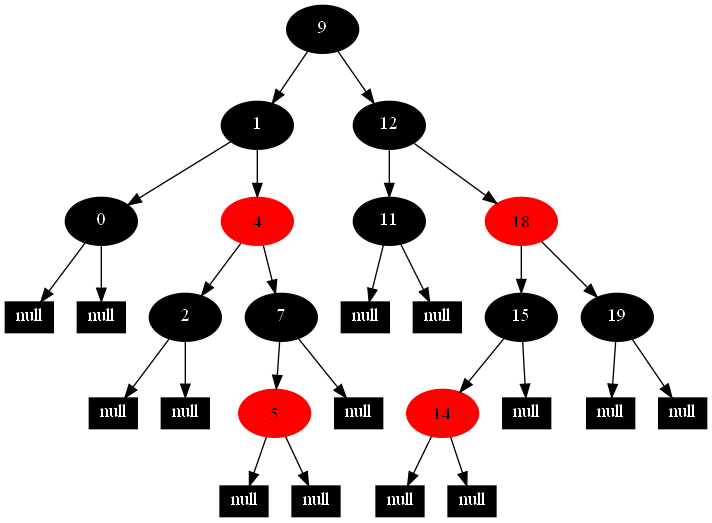
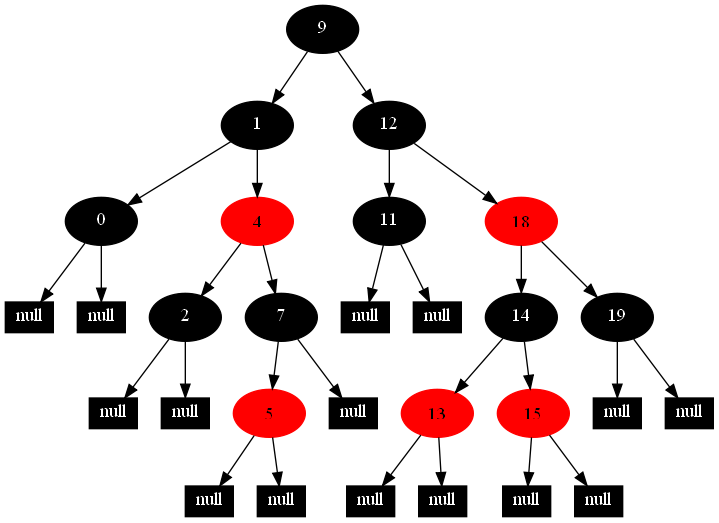
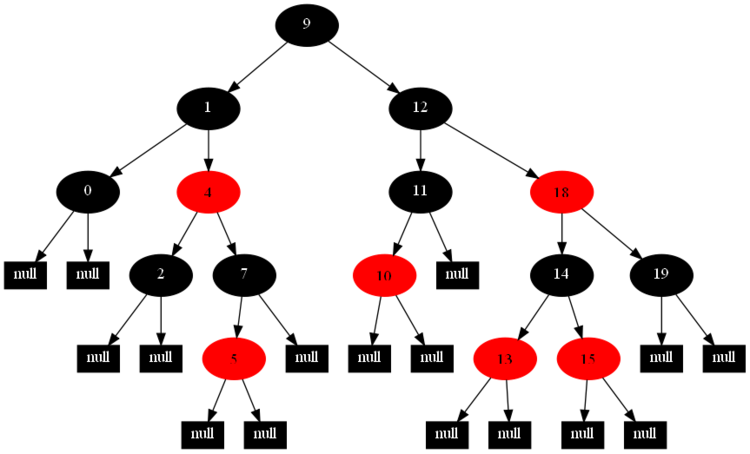
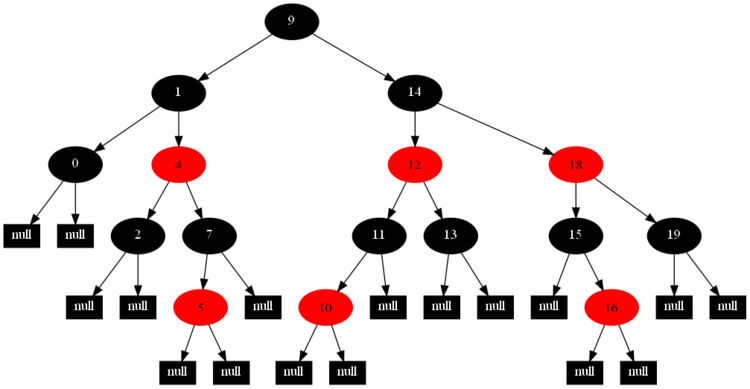
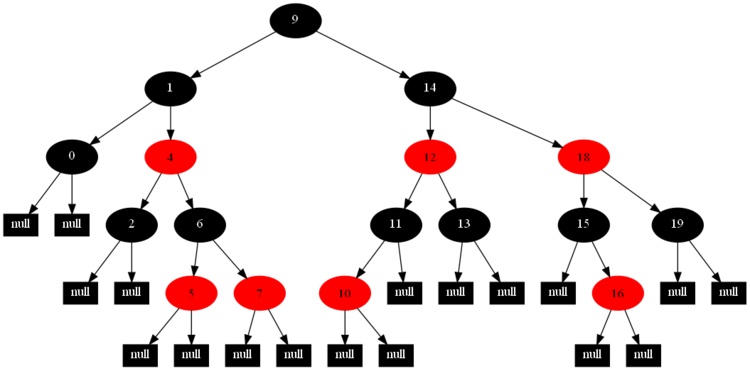
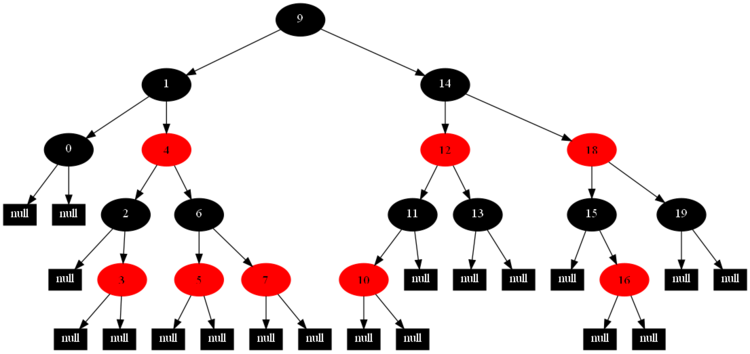
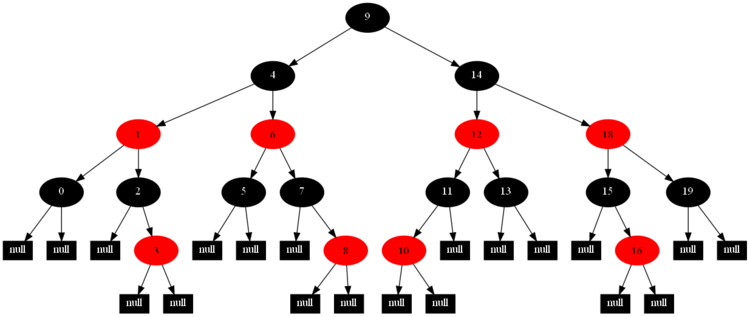
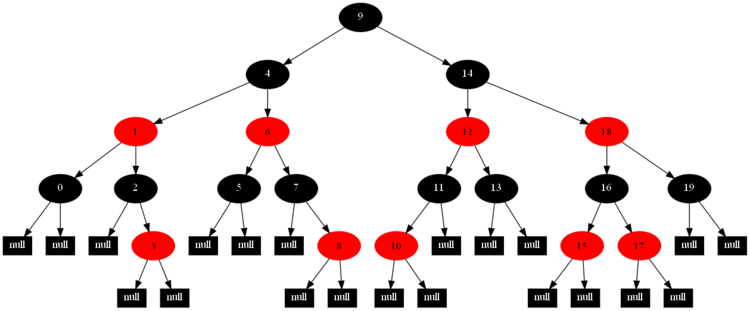
紅黑樹的一一插入各結點：12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示圖完。

紅黑樹刪除情況全過程演示
    紅黑樹的所有刪除情況，如下：

情況1: N 是新的根。
情形2：兄弟節點S是紅色
[對應我第二篇文章中，情況1：x的兄弟w是紅色的。]
情況 3: 兄弟節點S是黑色的，且S的倆個兒子都是黑色的。但N的父節點P，是黑色。
[對應我第二篇文章中，情況2：x的兄弟w是黑色的，且兄弟w的倆個兒子都是黑色的。
(這裡，N的父節點P為黑)]
情況4: 兄弟節點S 是黑色的、S 的兒子也都是黑色的，但是 N 的父親P，是紅色。
[還是對應我第二篇文章中，情況2：x的兄弟w是黑色的，且w的倆個孩子都是黑色的。
(這裡，N的父節點P為紅)]
情況5: 兄弟S為黑色，S 的左兒子是紅色，S 的右兒子是黑色，而N是它父親的左兒子。
//此種情況，最後轉化到下面的情況6。
[對應我第二篇文章中，情況3：x的兄弟w是黑色的，w的左孩子是紅色，w的右孩子是黑色。]
情況6: 兄弟節點S是黑色，S的右兒子是紅色，而 N 是它父親的左兒子。
[對應我第二篇文章中，情況4:x的兄弟w是黑色的，且w的右孩子時紅色的。]

    接下來，便是一一刪除這些點12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17為例，即，紅黑樹刪除情況全程演示：

    各個結點刪除與以上的六種情況，一一對應起來，如圖：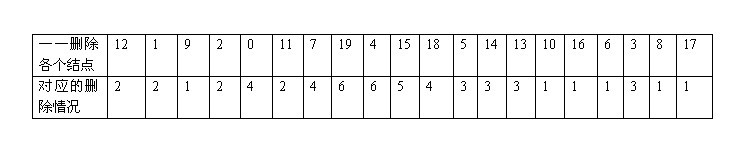

首先，插入12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17結點後，形成的紅黑樹為：

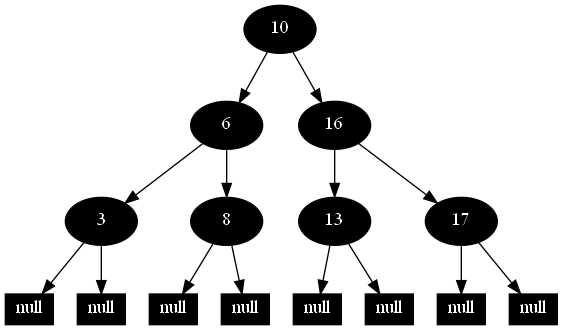
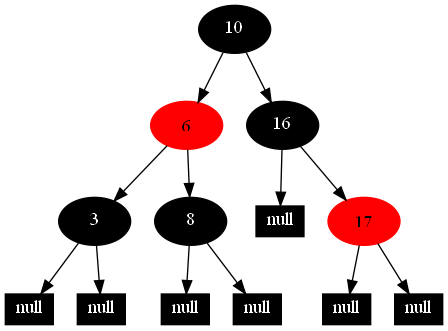
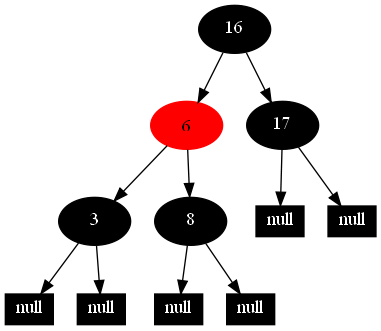
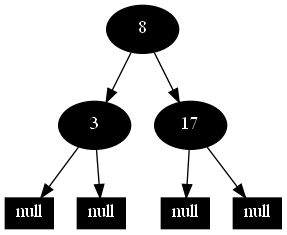
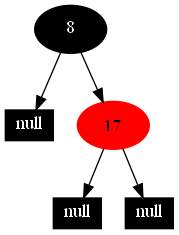
然後，以下的20張圖，是一一刪除這些結點12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17所得到的刪除情況的全程演示圖：

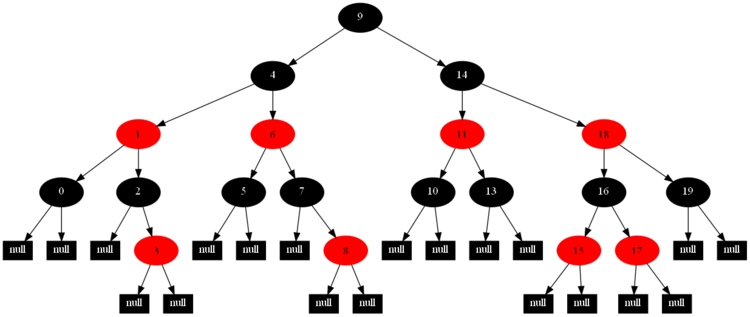
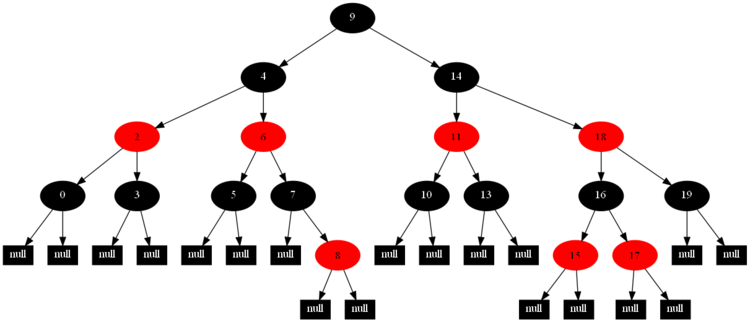
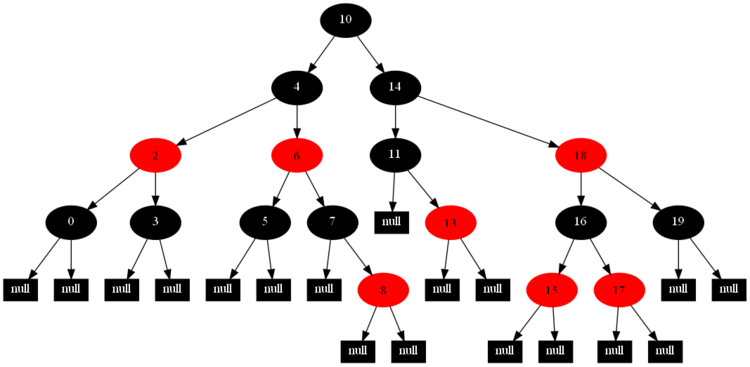
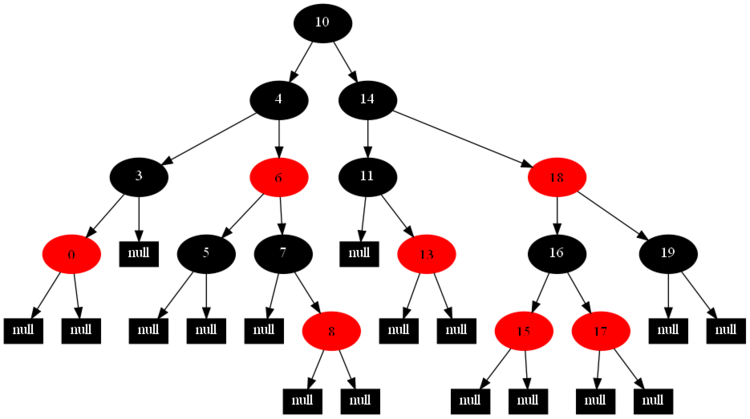
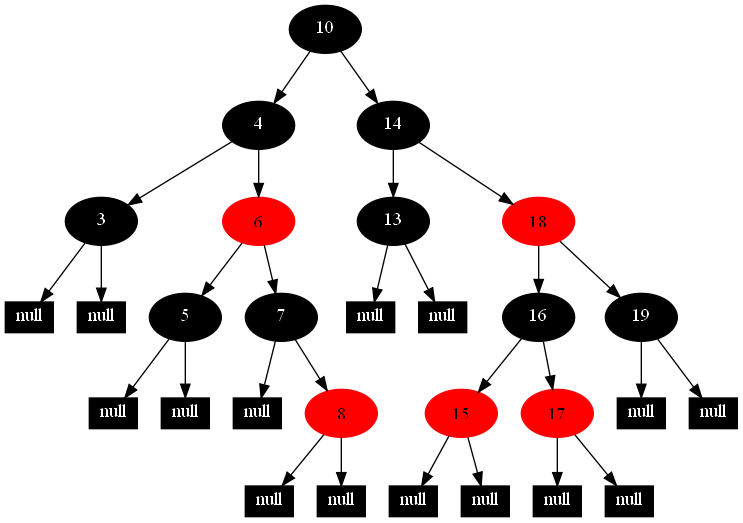
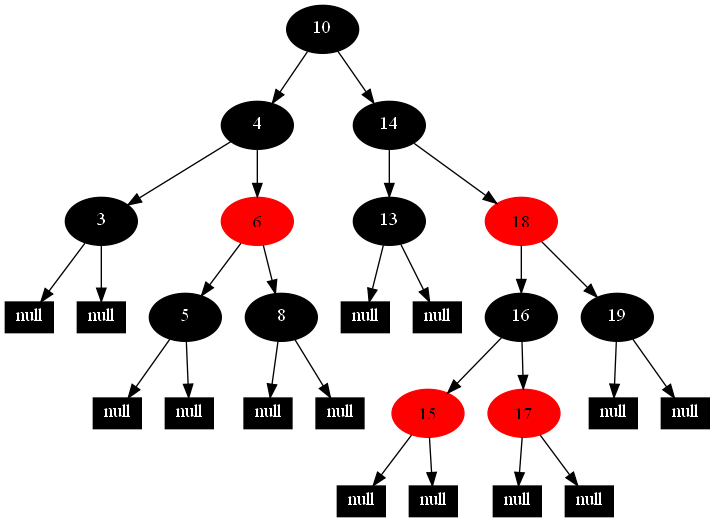
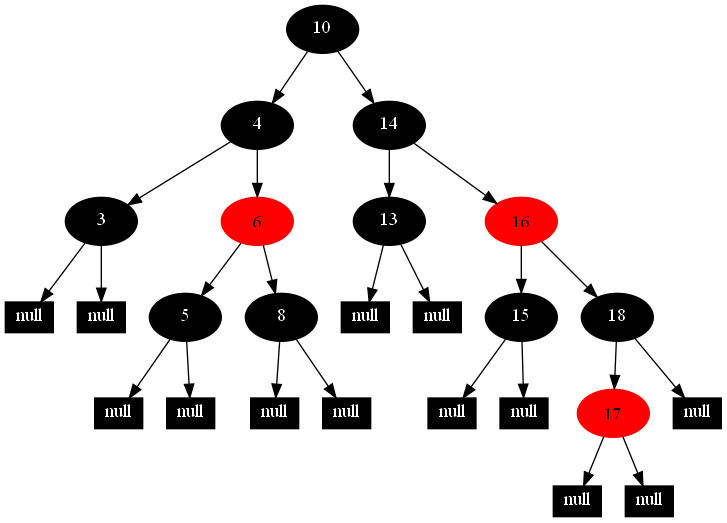
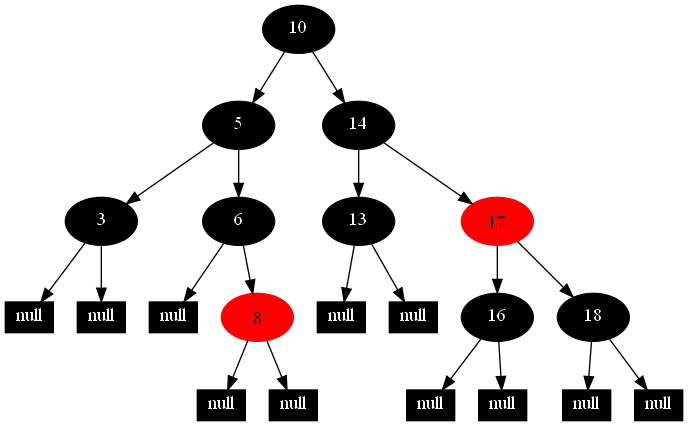
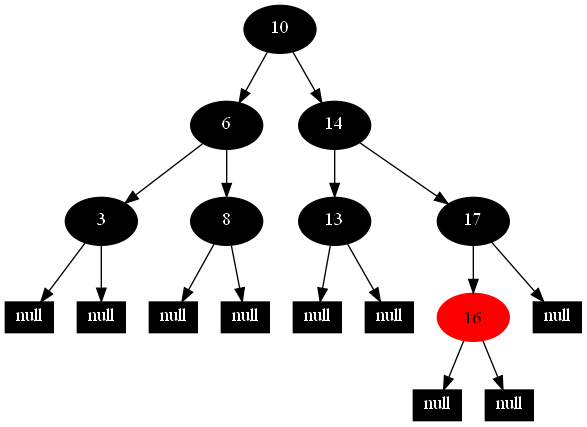
紅黑樹的一一刪除各結點：12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17的全程演示圖完。

參考文獻，本人代表作之一：紅黑樹系列：

全文完。