紅黑樹 節點的刪除
接上一篇。
紅黑樹的刪除繼續分各種情況進行考慮。
首先考慮紅黑樹的單支情況,即只有父節點只有一個子節點,另外一個為NULL,這樣的話,只有一種情況,即父節點為黑色,子節點為紅色,因為其他情況都會是孩子為黑色,因為孩子為紅色父為紅色,則與紅父黑子矛盾。而當孩子是黑色時,另一個孩子是黑色的NULL,則必定使左右路徑上黑色節點數量不等。所以單支只能為黑父紅子。
這裡的單支情況,是對任意一點的,若其只有一個孩子,則其必為黑色,孩子必為紅色,且孩子為葉子節點。孩子為紅色,如果有孫子,其孫子必為黑色,則路徑黑子數量不等,不平衡。
情況一:
單支,刪除紅色節點,則不會影響其他路徑情況,不影響平衡,直接刪除即可。
情況二:
單支,刪除黑節點
若s節點為黑色,則用單支下的紅色孩子替代自己,然後刪除黑色節點,這樣路徑上少了一個黑色節點,影響平衡,需要進行調整。
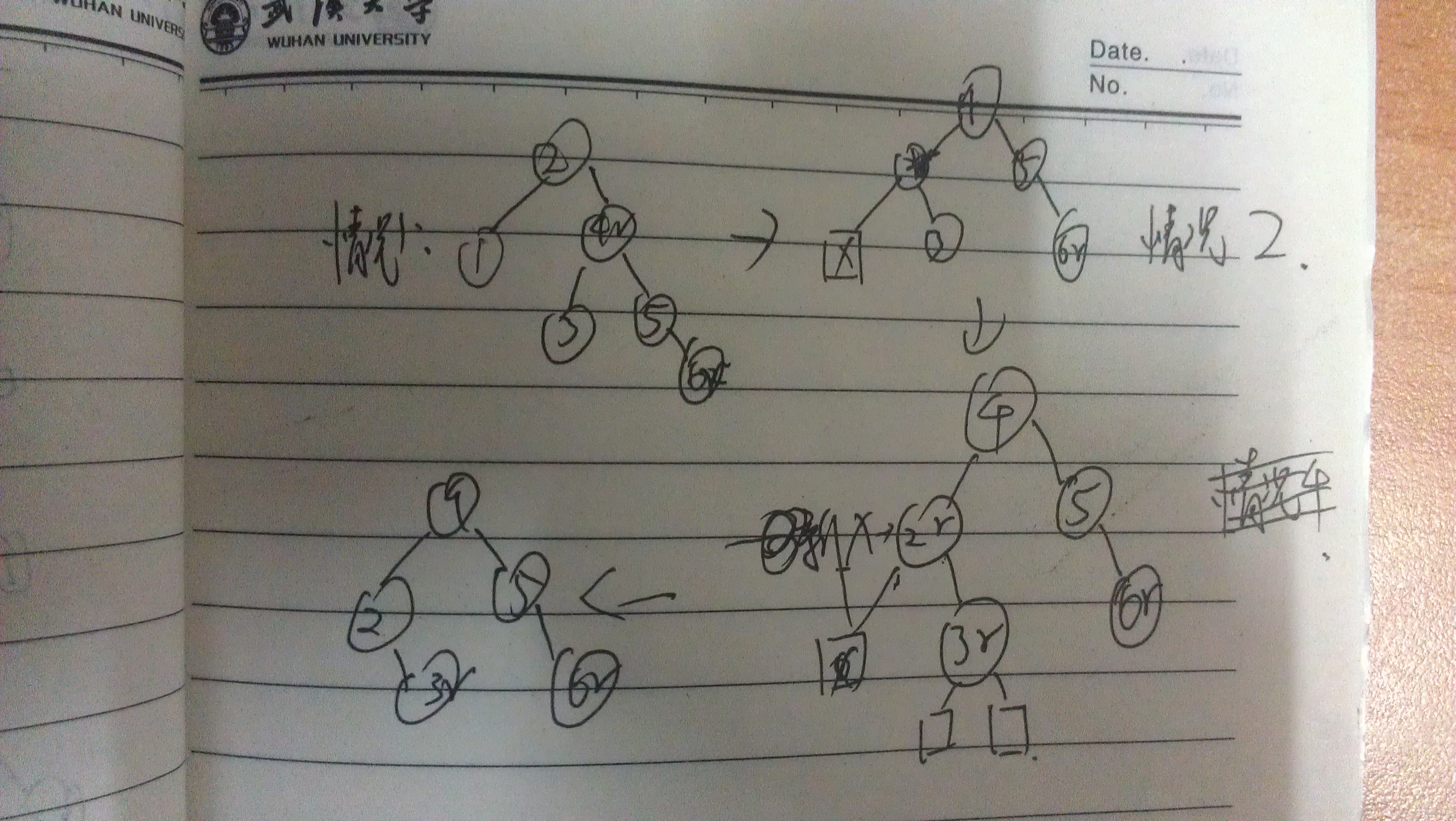
情況三:
刪除節點有兩個非空孩子,這時候又用到向下旋轉的思路,尋找刪除節點p的中序遍歷的後繼節點s,即正常排序後位於p之後的數字,而且s節點必定最多有一顆子樹,即s最多有一顆右子樹,或者沒有。若s節點有一顆右子樹,則必為單支情況,其孩子為紅色,且無孫子,則這就是情況二,轉到情況二。若s節點為葉子節點,則其可為紅色或黑色,紅色為情況一。
這種情況將p與s的資料交換,但顏色不換,則情況轉換為刪除s點,而刪除之前樹還是平衡的。
或者這樣分析:
若s節點為紅色,則其必定不是單支,則其為葉子節點,則是情況一,直接刪除即可。
若s節點為黑色,則用s的孩子null或者單支下的紅色孩子替代自己,然後刪除黑色節點,這樣路徑上少了一個黑色節點,影響平衡,需要進行調整。(這裡又要注意,如果是孩子為NULL,替代後,如何找到s節點的父節點。沒有哨兵節點,這個地方麻煩了。。。。好吧,呼叫的遞迴調整函式的引數加一個父節點指標)
然後如同插入一樣設定一個遞迴的調整函式,調整有4種情況:
首先以刪除判斷節點為x,為黑色,父節點為p,兄弟節點為w。以x為根的子樹的黑色節點樹減一,則需要進行平衡操作。
一般是有一下4種情況,但,還有一個特殊情況,即x為根節點時,跟插入時判斷相同,如果x為根節點,且現在為紅色, 則將其改為黑色。對於以下情況2,可能轉換到這種情況。第二次被別人的部落格坑,等會寫完了再測試有沒有其他錯誤。
情況1:w為紅色。
則w的孩子都為黑色,p為黑色。改變w和p的顏色,即w改為黑色,p改為紅色,然後以p為支點進行左旋,或右旋,根據x位於p的位置決定,若x為左孩子,左旋,右孩子右旋。更新後x獲得了新的兄弟節點,然後繼續對x進行判斷調節。
情況2:w為黑色,且w的孩子都為黑色。這裡由於之前是在x所在子樹上刪除了一個黑色的節點,則w所在子樹上必定有一個黑色節點,即w必定不為NULL。
將w置為紅色,使w所在子樹上黑色數量減一,則p所在子樹上黑色節點數量也減一,則需要以p節點作為當前節點,即新的x節點。如果新的x為紅,則將其置為黑色,則整個樹平衡,結束,如果為黑,則繼續判斷新的x節點的情況。
情況3:w為黑色。
如果x為p的左孩子, w的左孩子為紅色,右孩子為黑色。
則將w置為紅色,左孩子為黑色,然後以w節點為支點右旋。
如果x為p的右孩子, w的右孩子為紅色,左孩子為黑色、
則將w為紅,右孩子為黑,然後以w節點左旋。
獲得新的兄弟節點,進入情況4. 這裡進行情況3的旋轉不會對改變任何子樹的平衡性。
情況4:w為黑色。
如果x為p的左孩子,w的右孩子為紅色,左孩子可以為紅色或黑色或NULL。
則交換w和p的顏色,因為之後w要成為新的父節點,所以要獲得原來p的顏色,防止與p的父節點衝突。
將w的右孩子設定為黑色,這樣w的右子樹黑色節點樹+1,
再以p節點為支點左旋,這樣w的顏色黑色會移動到左子樹,使其節點樹 -1 + 1 =0,而右子樹減少了一個黑節點 +1 -1 = 0;且新的p節點為原來的顏色,整個樹是平衡的。結束、
如果x為p的右孩子,w的左孩子是紅色。同理、
交換w和p的顏色,將w的做孩子改為黑色,以p為節點右旋。結束判斷。
最終調整完成。這裡也有一個很重要的地方,在左旋和右旋時交換父節點p與其對應左右孩子c的顏色,導致旋轉後得到的新父節點p顏色未變,則不用再向上檢測。
中間測試的時候有出錯了,嘗試畫了一些圖並找出了錯誤,只畫了一張圖,其他都是看別人的部落格思考的。
刪除其實也不是特別複雜,嘗試寫出程式碼:
template <typename T>
void RBTree<T>::GetParentLinked(RBNode<T> *a,RBNode<T> *b){
if(a == root){
root = b;
if(b)
b->parent = 0;
return;
}
if(a->parent->left == a){
a->parent->left = b;
if(b)
b->parent = a->parent;
}else{
a->parent->right = b;
if(b)
b->parent = a->parent;
}
}
template <typename T>
bool RBTree<T>::Delete(const T &x){
RBNode<T> *p = root ,*s,*fa;
if(!root)return false;
while(p){
if(p->value == x)break;
else if(x < p->value)p = p->left;
else p = p->right;
}
if(p){
if( p->left && p->right){//當存在左右孩子時,向下旋轉
s = p->right;
while(s->left){
s = s->left;
}
int temp = p->value;
p->value = s->value;
s->value = temp;
p = s;
}
if(p->red){//為紅色葉子節點,直接刪除
GetParentLinked(p,p->left);
delete p;
}else{//為黑色時,將其紅色子孩子替代他
//由於之前已經向下旋轉,則這裡只有一種特殊可能,即單支情況刪除黑色根節點。
fa = p->parent;//之後可能沒有父節點。
if(p->left){
s = p->left;
GetParentLinked(p,p->left);
}
else {
s = p->right;
GetParentLinked(p,p->right);
}
delete p;
AdjustAfterDelete(s,fa);
}
return true;
}else return false;
}
template <typename T>
void RBTree<T>::AdjustAfterDelete(RBNode<T> *x ,RBNode<T> *p){
if(p){//如果有父指標,則有四種情況。
RBNode<T> *w ;
bool inLeftTree = true;//標記左右情況,左右情況不同旋轉方向以及判斷方式也不同。
if(p->left == x)w = p->right;
else {
w = p->left;
inLeftTree = false;
}
if(w->red){
w->red = false;
p->red = true;
if(inLeftTree)
LRotation(p);//以p為支點進行旋轉,不用考慮當前節點是否為空。
else
RRotation(p);
AdjustAfterDelete(x,p);
}else{
if( !GetColorWithNULL(w->left) && !GetColorWithNULL(w->right) ){
w->red = true;
x = p;
if(x ->red)x->red = false;//出錯一次,要根據新的x節點進行判斷。
else AdjustAfterDelete(x,x->parent);
}else if(( inLeftTree && GetColorWithNULL(w->right) ) //情況4
|| ( !inLeftTree && GetColorWithNULL(w->left) ) ){
bool tempRed = p->red;
p->red = w->red;
w->red = tempRed;
if(inLeftTree){
w->right->red = false;
LRotation(p);
}else{
w->left->red = false;
RRotation(p);
}
}else {//情況3
w->red = true;
if(inLeftTree){
w->left->red = false;
RRotation(w);
AdjustAfterDelete(x,p);
}else{
w->right->red = false;
LRotation(w);
AdjustAfterDelete(x,p);
}
}
}
}else{//如果不存在父節點,則此節點為根節點,則置為黑色結束。
if(x)
x->red = false;
return ;
}
}