簡單易懂帶你瞭解二叉樹
前言
上一篇部落格為大家介紹了陣列與連結串列這兩種資料結構,雖然它們在某些方面有著自己的一些優點,但是也存在著一些自身的缺陷,本篇部落格為將為大家介紹一下資料結構---二叉樹,它在保留陣列和連結串列的優點的同時也改善了它們的缺點(當然它也有著自己的缺點,同時它的實現也比較複雜).
1. 陣列和連結串列的特點
陣列的優點:
- 簡單易用.
- 無序陣列的插入速度很快,效率為O(1)
- 有序陣列的查詢速度較快(較無序陣列),效率為O(logN)
陣列的缺點:
- 陣列的查詢、刪除很慢
- 陣列一旦確定長度,無法改變
連結串列的優點:
- 可以無限擴容(只要記憶體夠大)
- 在連結串列頭的新增、刪除很快,效率為O(1)
連結串列的缺點:
- 查詢很慢
- 在非連結串列頭的位置新增、刪除很慢,效率為O(N)
2.樹和二叉樹
樹是一種資料結構,因為它資料的儲存形式很像一個樹,所以得名為樹(樹狀圖).
而二叉樹是一種特殊的樹,它的每個節點最多含有兩個子樹,現實世界中的二叉樹:

圖1
但是實際中的二叉樹卻是倒掛的,如圖:

圖2
二叉樹的名詞解釋:
- 根:樹頂端的節點稱為根。一棵樹只有一個根,如果要把一個節點和邊的集合稱為樹,那麼從根到其他任何一個節點都必須有且只有一條路徑。A是根節點。
- 父節點:若一個節點含有子節點,則這個節點稱為其子節點的父節點;B是D的父節點。
- 子節點:一個節點含有的子樹的根節點稱為該節點的子節點;D是B的子節點。
- 兄弟節點:具有相同父節點的節點互稱為兄弟節點;比如上圖的D和E就互稱為兄弟節點。
- 葉節點:沒有子節點的節點稱為葉節點,也叫葉子節點,比如上圖的E、H、L、J、G都是葉子節點。
- 子樹:每個節點都可以作為子樹的根,它和它所有的子節點、子節點的子節點等都包含在子樹中。
- 節點的層次:從根開始定義,根為第一層,根的子節點為第二層,以此類推。
- 深度:對於任意節點n,n的深度為從根到n的唯一路徑長,根的深度為0;
- 高度:對於任意節點n,n的高度為從n到一片樹葉的最長路徑長,所有樹葉的高度為0;
深度與高度的區別在於: 深度為根到節點的距離,而高度是節點到葉的距離(記住根深葉高)。
3.二叉搜尋樹以及它是通過什麼方式改善的陣列、連結串列的問題
二叉搜尋樹是一種特殊的二叉樹,除了它的子節點不能超過兩個以外,它還擁有如下特點:
- 一個節點的左子節點的關鍵字的值永遠小於該節點的值
- 一個節點的右子節點的關鍵字的值永遠大於等於該節點的值
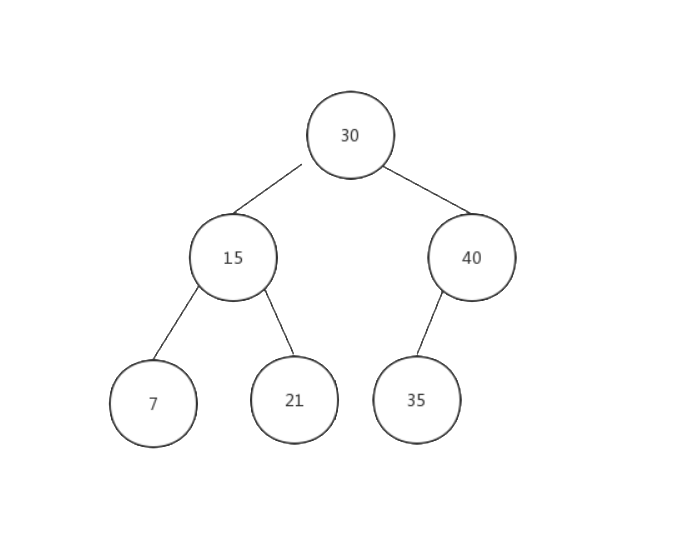
圖3 - 二叉搜尋樹關鍵字的排序方式
從圖3還可以看出,二叉搜尋樹的最小值就是它的最左節點的關鍵字的值,而最大值則是它的最右節點的值.
二叉搜尋樹的查詢、新增、刪除的效率為O(logN)(這是理想狀態下,如果樹是不平衡的效率會降到O(N),後面會介紹).
二叉搜尋樹之所以效率高就在於:
- 它的資料是按照上述的有序的方式排列的.
- 進行新增、查詢、刪除的時候使用了二分查詢法.
4. 二叉樹的實現
二叉樹中資料是儲存在一個個的節點中的,下面是儲存資料的節點類:
/**
* @author liuboren
* @Title: 節點類
* @Description:
* @date 2019/11/28 9:33
*/
public class Node {
// 用來進行排序的關鍵字陣列
int sortData ;
// 其他型別的資料
int other;
// 該節點的左子節點
Node leftNode;
// 該節點的右子節點
Node rightNode;
public static void main(String[] args) {
Node node = new Node();
System.out.println("node.leftNode = " + node.leftNode);
System.out.println(node.leftNode);
}
}在二叉搜尋樹這個類中新增、修改、刪除資料:
public class Tree {
// 根節點
Node root;
public Tree(Node root) {
this.root = root;
}
// 新增、查詢、刪除 暫時省略,下面會一一介紹
}4.1 新增資料
在二叉樹中插入資料的流程如下:
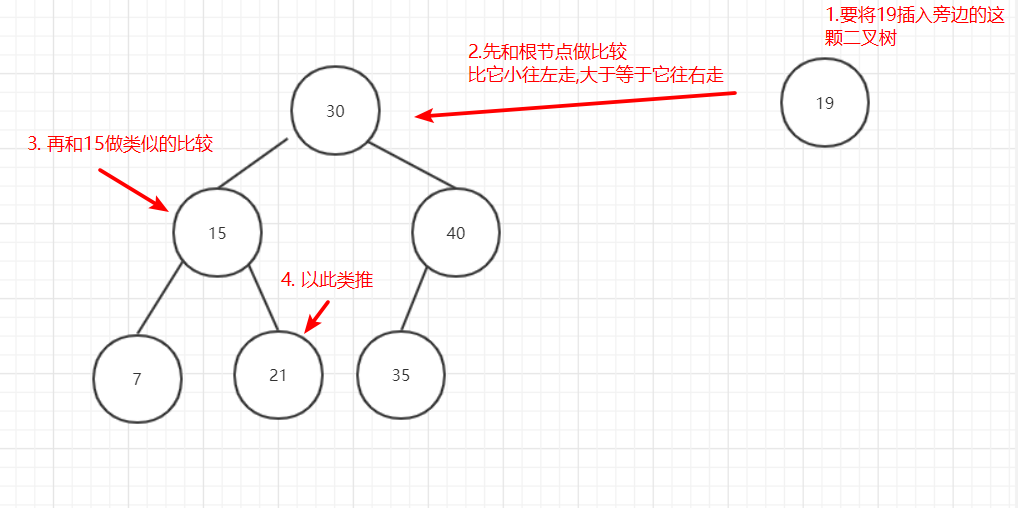
圖4
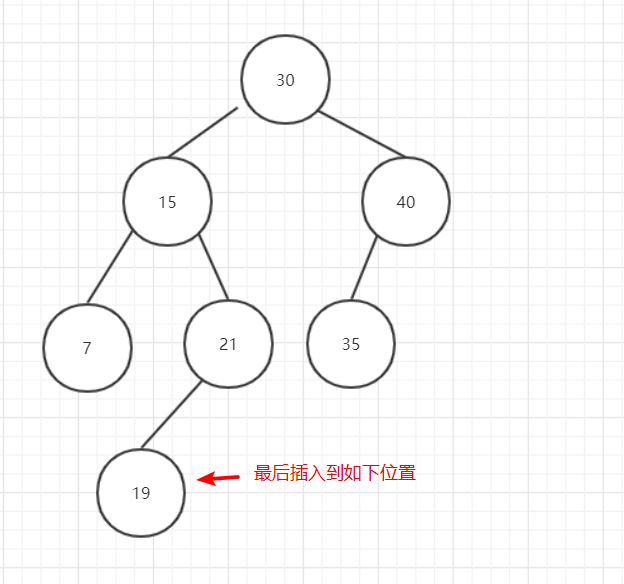
圖5
Java程式碼:
/*新增資料*/
public void insertData(Node node) {
int currentSortData = root.sortData;
Node currentNode = root;
Node currentLeftNode = root.leftNode;
Node currentRightNode = root.rightNode;
int insertSortData = node.sortData;
while (true) {
if (insertSortData < currentSortData) {
if (currentLeftNode == null) {
currentNode.leftNode = node;
break;
} else {
currentNode = currentNode.leftNode;
currentSortData = currentNode.sortData;
}
} else {
if (currentRightNode == null) {
currentNode.rightNode = node;
break;
} else {
currentNode = currentNode.rightNode;
currentSortData = currentNode.sortData;
}
}
}
System.out.println("root = " + root);
}4.3 查詢方法
流程與插入方法類似.
Java程式碼:
public void query(int sortData) {
Node currentNode = root;
while (true) {
if (sortData != currentNode.sortData) {
if (sortData < currentNode.sortData) {
if (currentNode.leftNode != null) {
currentNode = currentNode.leftNode;
} else {
System.out.println("對不起沒有查詢到資料");
}
} else {
if (currentNode.rightNode != null) {
currentNode = currentNode.rightNode;
} else {
System.out.println("對不起沒有查詢到資料");
}
}
} else {
System.out.println("二叉樹中有該資料");
}
}
}4.3 刪除方法
刪除節點要分三種情況.
- 刪除節點無子節點的情況
- 刪除節點有一個子節點的情況
- 刪除節點有兩個子節點的情況
刪除節點無子節點的情況是最簡單的,直接將該節點置為null就可以了:
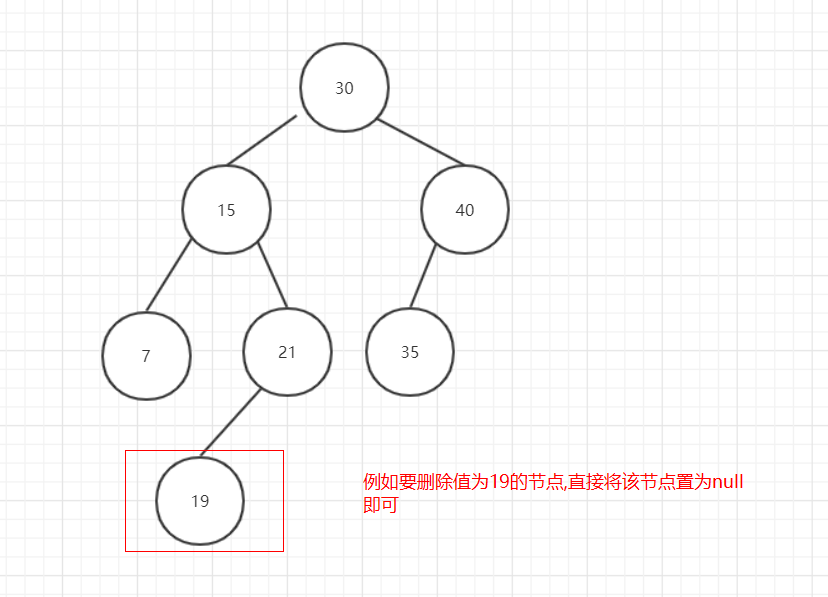
圖6
刪除節點有一個子節點的情況:

圖7
刪除後:
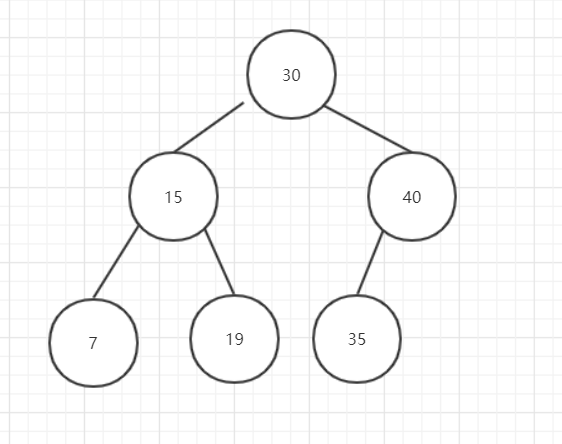
圖8
最複雜的刪除節點有兩個子節點的情況,刪除流程如下:
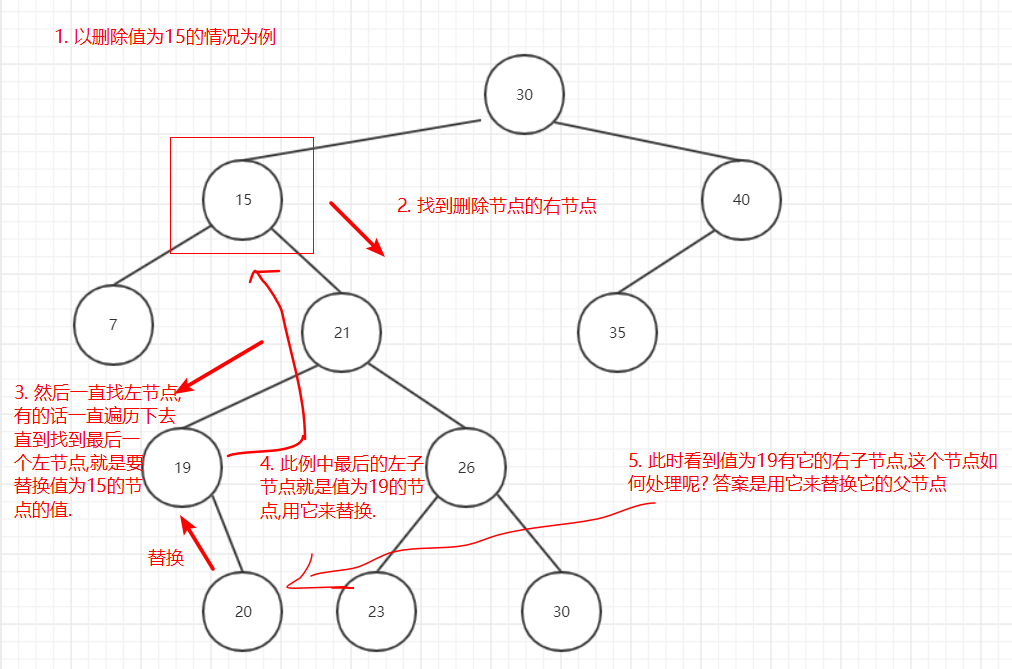
圖9
刪除後:
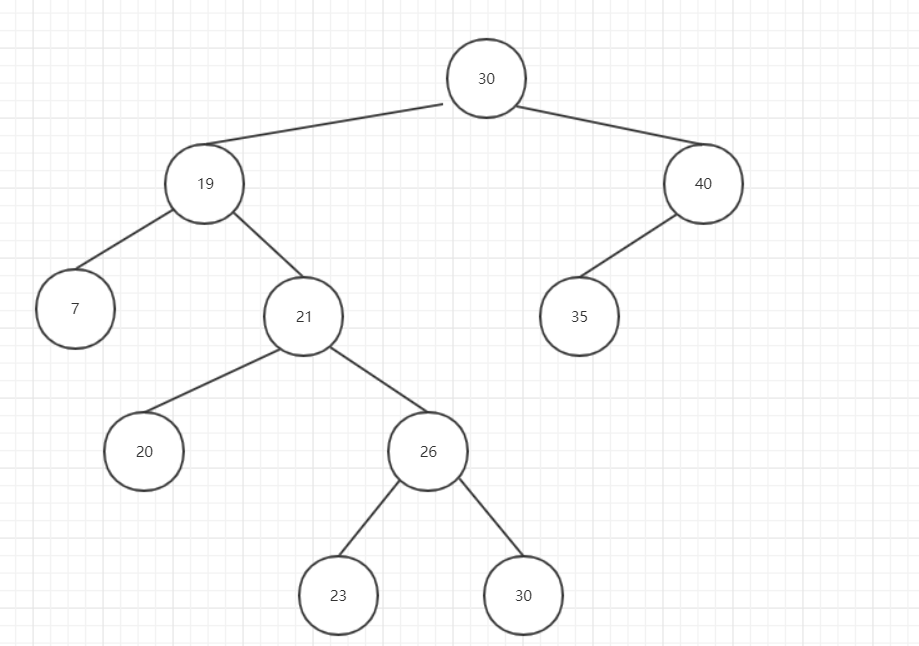
圖10
為什麼要以這種方式刪除節點呢? 再次回顧一下二叉搜尋樹的特點:
- 一個節點的左子節點的關鍵字的值永遠小於該節點的值
- 一個節點的右子節點的關鍵字的值永遠大於等於該節點的值
之所以要找刪除節點的右子節點的最後一個左節點,是因為這個值是刪除節點的子節點中最小的值,為了滿足上面的這兩個特點,所以刪除要以這種演算法去實現.
Java程式碼:
public boolean delete(int deleteData) {
Node curr = root;
Node parent = root;
boolean isLeft = true;
while (deleteData != curr.sortData) {
if (deleteData <= curr.sortData) {
isLeft = true;
if (curr.leftNode != null) {
parent = curr;
curr = curr.leftNode;
}
} else {
isLeft = false;
if (curr.rightNode != null) {
parent = curr;
curr = curr.rightNode;
}
}
if (curr == null) {
return false;
}
}
// 刪除節點沒有子節點的情況
if (curr.leftNode == null && curr.rightNode == null) {
if (curr == root) {
root = null;
} else if (isLeft) {
parent.leftNode = null;
} else {
parent.rightNode = null;
}
//刪除節點只有左節點
} else if (curr.rightNode == null) {
if (curr == root) {
root = root.leftNode;
} else if (isLeft) {
parent.leftNode = curr.leftNode;
} else {
parent.rightNode = curr.leftNode;
}
//如果被刪除節點只有右節點
} else if (curr.leftNode == null) {
if (curr == root) {
root = root.rightNode;
} else if (isLeft) {
parent.leftNode = curr.rightNode;
} else {
parent.rightNode = curr.rightNode;
}
} else {
Node successor = getSuccessor(curr);
if (curr == root) {
root = successor;
} else if (curr == parent.leftNode) {
parent.leftNode = successor;
} else {
parent.rightNode = successor;
}
successor.leftNode = curr.leftNode;
}
return true;
}
public Node getSuccessor(Node delNode) {
Node curr = delNode.rightNode;
Node successor = curr;
Node sucParent = null;
while (curr != null) {
sucParent = successor;
successor = curr;
curr = curr.leftNode;
}
if (successor != delNode.rightNode) {
sucParent.leftNode = successor.rightNode;
successor.rightNode = delNode.rightNode;
}
return successor;
}
5. 遍歷
遍歷二叉樹中的資料,有三種遍歷方式:
- 前序
- 中序(最常用)
- 後續
前序、中序和後序三種遍歷方式的步驟是相同的,只是順序不同.
前序遍歷順序:
- 先輸出當前節點
- 再遍歷左子節點
- 再遍歷右子節點
中序遍歷順序:
- 先遍歷左子節點
- 再輸出當前節點
- 再遍歷右子節點
後序遍歷順序:
- 先遍歷左子節點
- 再遍歷又子節點
- 再輸出當前節點
什麼當前節點?什麼左右子節點?太抽象!!!!沒關係繼續看圖.
前序遍歷輸出順序圖:
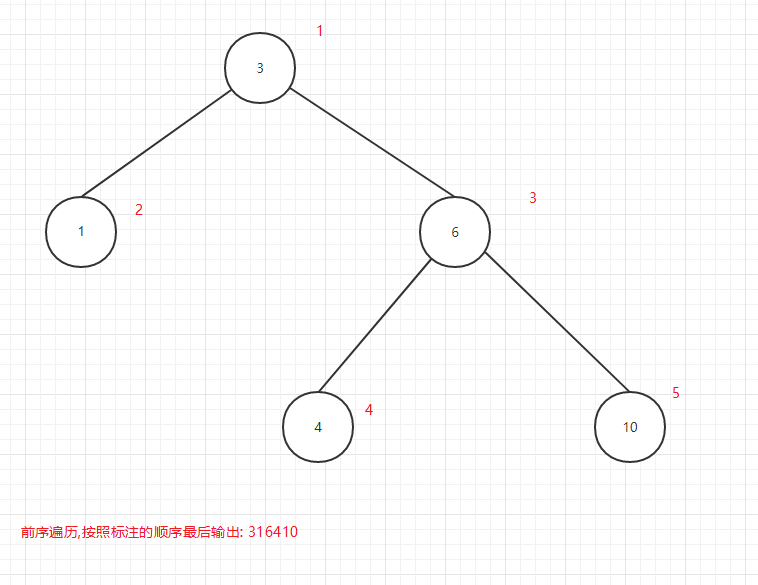
圖11
中序遍歷輸出順序圖:
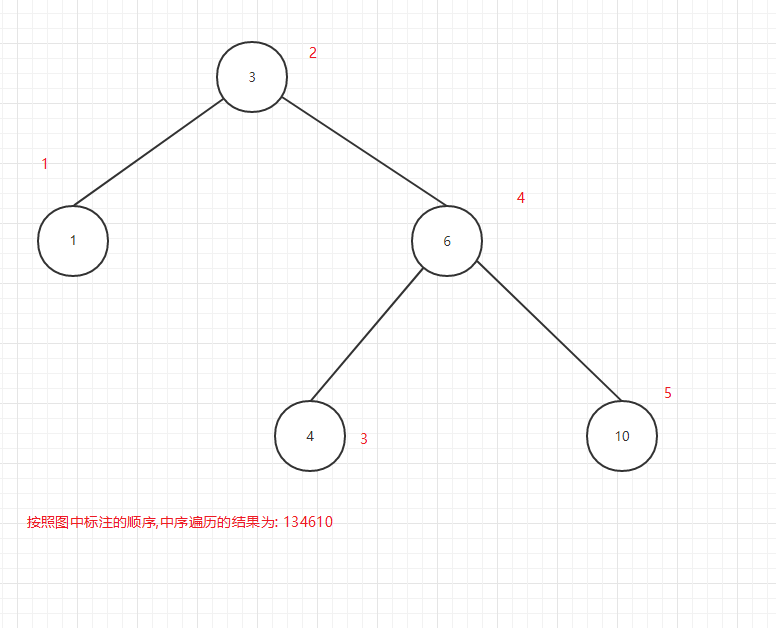
圖12
後序遍歷輸出順序圖:
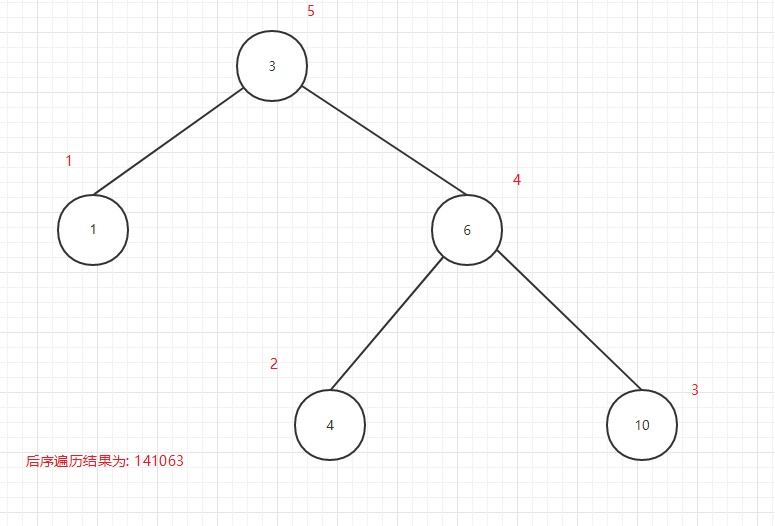
圖13
可以看出所謂的前中後序是輸出當前節點的順序,前序是在第一個輸出當前節點,中序是第二個輸出當前節點,後序是第三個當前節點.
又因為中序遍歷是按照關鍵值由小到大的順序輸出的,所以中序遍歷最為常用.
前、後序遍歷在解析或分析二叉樹(不是二叉搜尋樹)的算術表示式的時候比較有用,用的不太多,看下圖:
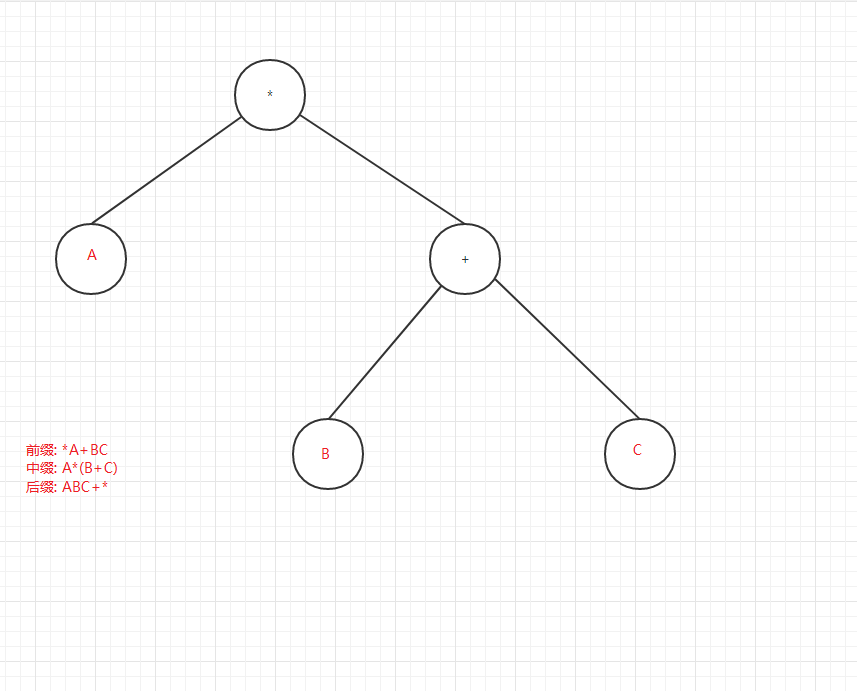
6. 二叉樹的效率
我們用二叉樹與陣列和連結串列進行對比,在有100w個數據項的無序陣列或連結串列中,查詢資料項平均會比較50w次,但在有100w個節點的樹中,只需要20(或更少)次的比較.
有序陣列可以很快的找到資料項,但插入資料項平均需要移動50w個數據項,在100w個節點的樹中插入資料項需要比較20或更少次的比較,再加上很短的時間來連線資料項.
同樣,從有100w個數據項的陣列中刪除一個數據項需要平均移動50w個數據項,而在100w個節點的樹中刪除節點只需要20次或更少的比較來找到它,再加上(可能的話)一點比較的時間來找到它的後繼,一點時間來斷開這個節點的連結,以及連線它的後繼.
結論: 樹對所有常用的資料儲存操作都有很高的效率
遍歷不如其他操作快. 但是,遍歷在大型資料庫中不是常用的操作.它更長用於程式中的輔助方法來解析算術或其他的表示式,而且表示式一般都不會很長.
如果二叉樹是平衡的,它的效率為: O(logN),如果二叉樹是不平衡的(最極端的情況,存入樹中的資料是升序或降序排列的,那麼二叉樹就是連結串列),效率為: O(N)
所以二叉搜尋樹在儲存隨機數值的時候,效率才是最高的
7. 二叉樹的缺點
如果二叉樹是極端不平衡的(此時的二叉樹就是一個連結串列),它的效率為O(N),即使數值是隨機的,如果資料的量夠大,也有可能有一部分的數值是有序的(就像你拋硬幣的時間足夠長,會有一段時間出現一隻拋正面或反面),造成二叉樹會變成使區域性不平衡的,這樣它的效率會介於O(logN)到O(N).
如何使二叉樹的效率始終保持在O(logN)呢? 下篇部落格為您介紹紅黑樹.
