背景描述

二叉樹遍歷相信大家在學習資料結構的時候都學習過，有遞迴方法和非遞迴方法，遞迴方法簡單，容易理解，不在本次的討論範圍內。因此本篇文章主要是討論非遞迴的方法，也就是迭代法。這種方法網上有很多解題方法，先序，後序，中序還都不一樣，很難理解。即便當時理解了，過段時間再讓你寫，你也是懵逼的。下面我將介紹一種方法，這種方法可以說利器，只要掌握了它的思想，你會發現先序，中序，後序，只是調整一行程式碼的順序，就都能解決出來，可謂是一招鮮，吃遍天。

方法描述

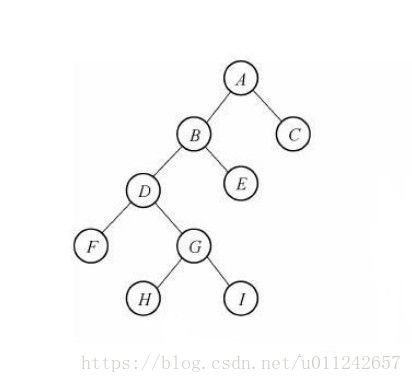
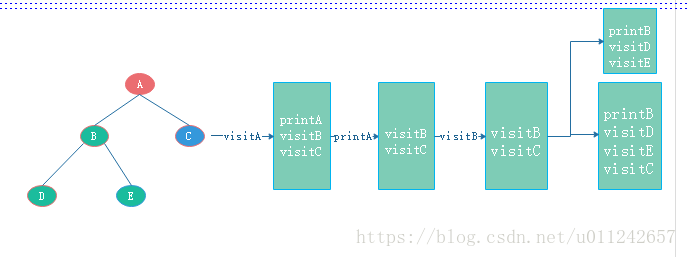
如圖是一棵二叉樹，我們以先序遍歷分析，我們訪問二叉樹中的節點可以看作三種操作，列印該節點，訪問該節點的左孩子，訪問該節點的右孩子。舉例說明，假如我們要訪問節點 A,那麼會分解為如下的操作 ：

• print A
• visit B

• visit C
  首先我們會列印A,然後訪問節點B,那麼訪問節點B又會被分解位三個操作

• print B

• visit D
• visit E
  
  上一張圖大家更容易理解，很明顯這需要一個數據結構佇列或者棧來實現

程式碼實現

這裡編寫程式碼的語言是Java，其他語言可以參照此思路進行編寫程式碼

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
 

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
         //存放結果
        List<Integer> result = new ArrayList<>();
        //宣告一個佇列
        Deque<Guide> path = new ArrayDeque<>();
        //將根節點放到隊首
        path.addFirst(new Guide(0,root));
        while
 
(!path.isEmpty()){
            //訪問佇列中的隊首元素
            Guide current = path.removeFirst();
            //這裡需要做判斷，因為空節點也被放進了佇列
            if(current.treeNode==null){
                continue;
            }
            //op= 1，說明是print該節點，遂將其放進結果容器中
            if(current.op==1){
                result.add(current.treeNode.val);
            }else{
              //訪問該節點，於是將該節點的三個操作放到佇列中 print 自己，visist 左孩子，visit右孩子
               path.addFirst(new Guide(0,current.treeNode.right));
               path.addFirst(new Guide(0,current.treeNode.left));
               path.addFirst(new Guide(1,current.treeNode)); 
            }    
        }
        return result;
    }
    private class Guide{
        //0 代表visit該節點,1 print 代表列印該節點
        int op;
        TreeNode treeNode;
        public Guide(int op,TreeNode node){
            this.op = op;
            this.treeNode = node;
        }

    }
}

這裡比較巧妙的是我們將節點和節點的操作封裝成一個物件存放到佇列中，對於一個節點要麼是被列印，要麼是被訪問。
注：這裡是用佇列來實現的，很明顯用棧也可以，只是和佇列的放入順序是相反的。（removeFirst相當於隊首元素出隊，addFirst相當於往佇列的隊頭加元素）
按照這種思路，中序遍歷和後序遍歷就很容易了，只需要動一行程式碼就可以搞定
中序遍歷：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<Guide> path = new ArrayDeque<>();
        path.addFirst(new Guide(0,root));
        while(!path.isEmpty()){
            //取出隊首元素
            Guide current = path.removeFirst();
            if(current.node==null) continue;
            if(current.op==1){
                result.add(current.node.val);
            }else{
                path.addFirst(new Guide(0,current.node.right));
                path.addFirst(new Guide(1,current.node));
                path.addFirst(new Guide(0,current.node.left));

            }
        }
        return result;
    }


    private class Guide{
         int op;
         TreeNode node;
        public Guide(int op, TreeNode node){
            this.op = op; //0 visit,1 print
            this.node = node;
        }

  }
}

後序遍歷

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<Guide> path = new ArrayDeque<>();
        path.addFirst(new Guide(0,root));
        while(!path.isEmpty()){
            //取出隊首元素
            Guide current = path.removeFirst();
            if(current.node==null) continue;
            if(current.op==1){
                result.add(current.node.val);
            }else{
                path.addFirst(new Guide(1,current.node));
                path.addFirst(new Guide(0,current.node.right));
                path.addFirst(new Guide(0,current.node.left));

            }
        }
        return result;
    }


    private class Guide{
         int op;
         TreeNode node;
        public Guide(int op, TreeNode node){
            this.op = op; //0 visit,1 print
            this.node = node;
        }
   }
}

總結

通過以上分析和程式碼的實現，我們發現，先序，中序，後序只需要根據其訪問的規則調整這三行程式碼的順序就可以了，其他程式碼一行都不用動。