目錄

• 一、平衡二叉樹定義
• 二、這貨還是不是平衡二叉樹？
• 三、平衡因子
• 四、如何保持平衡二叉樹平衡？
• 五、平衡二叉樹插入節點的四種情況
• 六、平衡二叉樹操作的程式碼實現
• 七、AVL樹總結

@

一、平衡二叉樹定義

平衡二叉樹又稱AVL樹。它可以是一顆空樹，或者具有以下性質的二叉排序樹：它的左子樹和右子樹的高度之差(平衡因子)的絕對值不超過1且它的左子樹和右子樹都是一顆平衡二叉樹。

從上面簡單的定義我們可以得出幾個重要的資訊：

• 平衡二叉樹又稱AVL樹
• 平衡二叉樹必須是二叉排序樹
• 每個節點的左子樹和右子樹的高度差至多為1。

在定義中提到了樹的高度和深度，我敢肯定有很多讀者一定對樹的高度和深度有所誤解！最可愛的誤解就是樹的高度和深度沒有區別，認為樹的高度就是深度。宜春就忍不了了，必須得嗶嗶幾句...

樹的高度和深度本質區別：深度是從根節點數到它的葉節點，高度是從葉節點數到它的根節點。

二叉樹的深度是從根節點開始自頂向下逐層累加的；而二叉樹高度是從葉節點開始自底向上逐層累加的。雖然樹的深度和高度一樣，但是具體到樹的某個節點，其深度和高度是不一樣的。

其次就是對樹的高度和深度是從1數起，還是從0數起。當然我也有自己的答案，但是眾說紛紜，博主就不說其對與錯了，就不多嗶嗶了。但是我還是比較認同這張圖的觀點：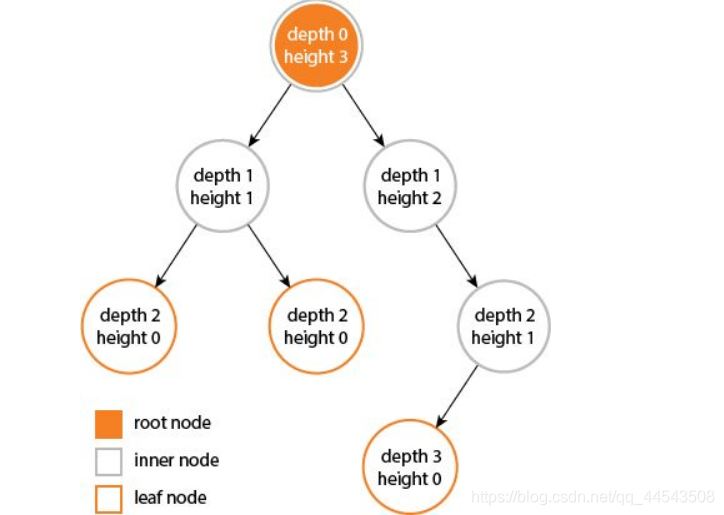

可參考：https://www.zhihu.com/question/40286584

二、這貨還是不是平衡二叉樹？

判斷一棵平衡二叉樹（AVL樹）有如下必要條件：

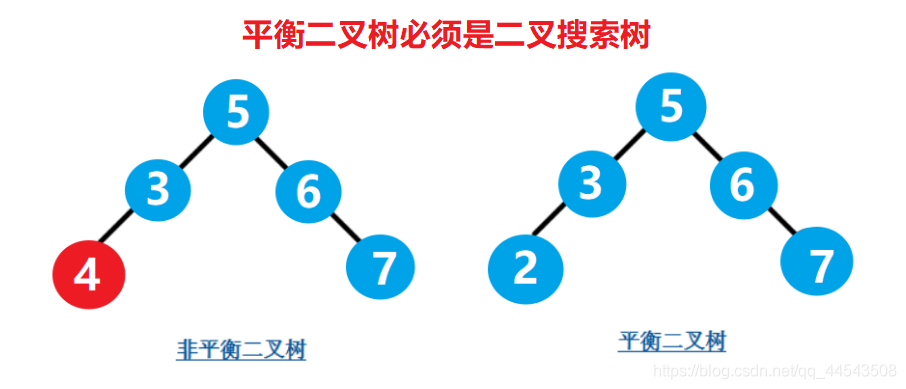
條件一：必須是二叉搜尋樹。
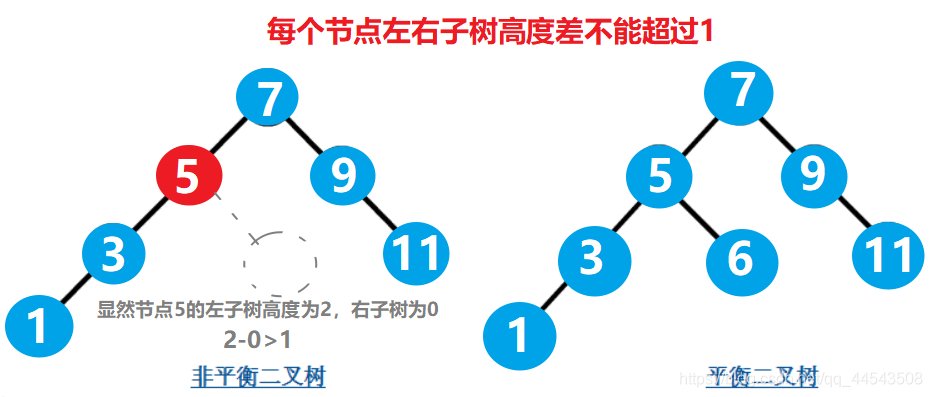
條件二：每個節點的左子樹和右子樹的高度差至多為1。

三、平衡因子

不多嗶嗶，平衡因子 = 左子樹深度/高度 - 右子樹深度/高度

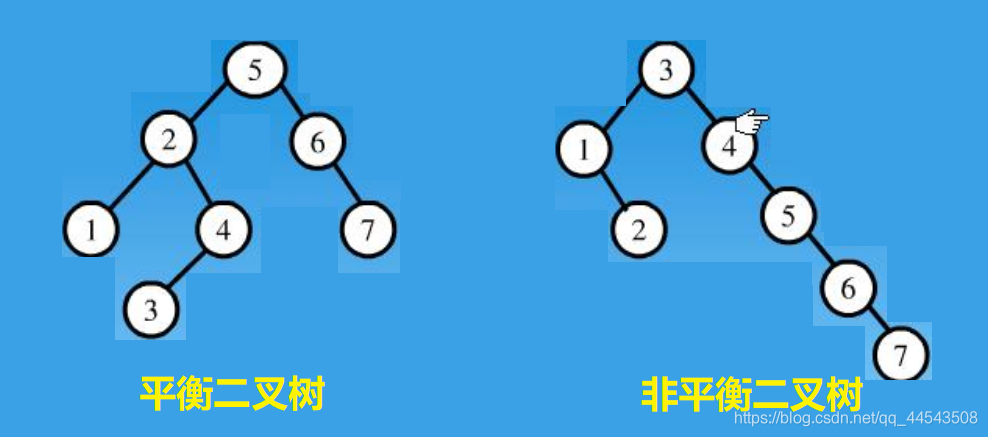
對於上圖平衡二叉樹而言：
5的結點平衡因子就是 3 - 2 = 1；
2的結點平衡因子就是 1 - 2 = -1；
4的結點平衡因子就是 1 - 0 = 1；
6的結點平衡因子就是 0 - 1 = -1；

對於上圖非平衡二叉樹而言：
3 的結點平衡因子就是 2 - 4 = -2；
1 的結點平衡因子就是 0 - 1 = -1；
4 的結點平衡因子就是 0 - 3 = -3；
5 的結點平衡因子就是 0 - 2 = -2；
6 的結點平衡因子就是 0 - 1 = -1；

特別注意：葉子結點平衡因子都是為 0

四、如何保持平衡二叉樹平衡？

由於普通的二叉查詢樹會容易失去”平衡“，極端情況下，二叉查詢樹會退化成線性的連結串列，導致插入和查詢的複雜度下降到 O(n) ，所以，這也是平衡二叉樹設計的初衷。那麼平衡二叉樹如何保持”平衡“呢？

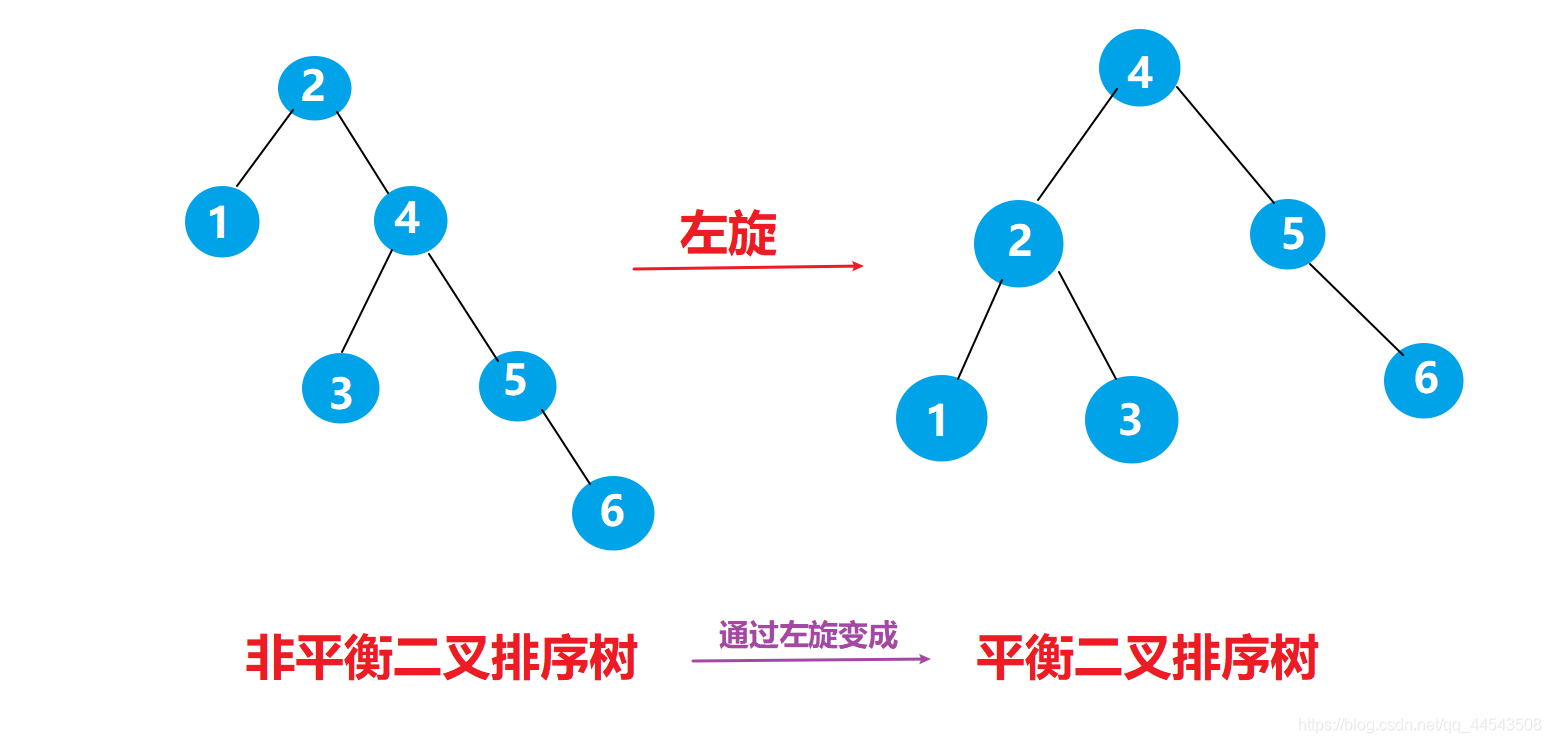
不難看出平衡二叉樹是一棵高度平衡的二叉查詢樹。所以，要構建跟維繫一棵平衡二叉樹就比普通的二叉樹要複雜的多。在構建一棵平衡二叉樹的過程中，當有新的節點要插入時，檢查是否因插入後而破壞了樹的平衡，如果是，則需要做旋轉去改變樹的結構。關於旋轉，我相信使用文字描述是很難表達清楚的，還是得靠經典的兩個圖來理解最好不過了！不要不信噢，當然你可以嘗試讀下文字描述左旋：

左旋簡單來說就是將節點的右支往左拉，右子節點變成父節點，並把晉升之後多餘的左子節點出讓給降級節點的右子節點。

相信你已經暈了。當然可以試著看看下面的經典動圖理解！

左旋：

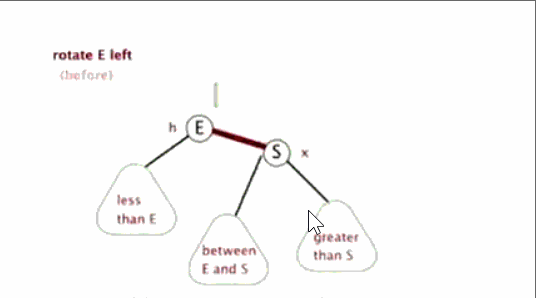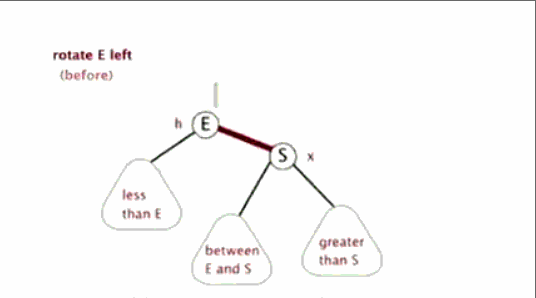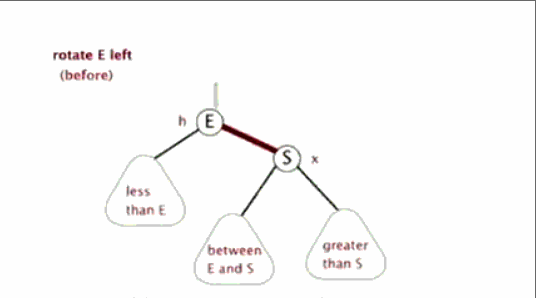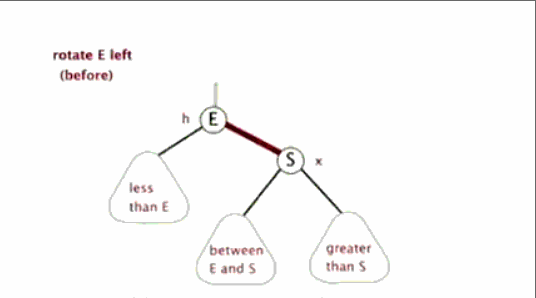
==試著用動態和下面的左旋結果圖分析分析，想象一下，估計分分鐘明白左旋！！！==

 //左旋轉方法程式碼
    private void leftRotate() {
        //建立新的結點，以當前根結點的值
        Node newNode = new Node(value);
        //把新的結點的左子樹設定成當前結點的左子樹
        newNode.left = left;
        //把新的結點的右子樹設定成帶你過去結點的右子樹的左子樹
        newNode.right = right.left;
        //把當前結點的值替換成右子結點的值
        value = right.value;
        //把當前結點的右子樹設定成當前結點右子樹的右子樹
        right = right.right;
        //把當前結點的左子樹(左子結點)設定成新的結點
        left = newNode;
    }

相應的右旋就很好理解了：

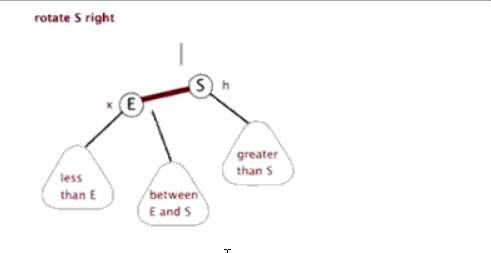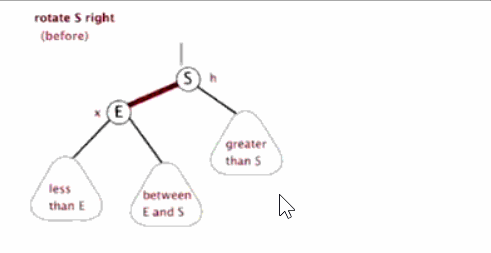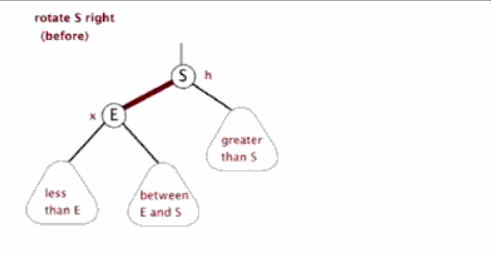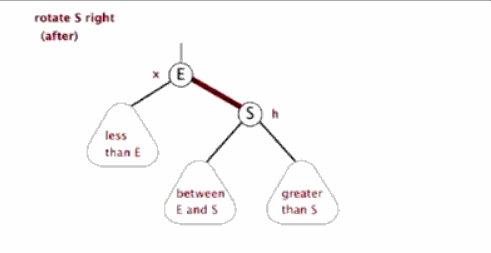
反之就是右旋，這裡就不再舉例了！

小結：當二叉排序樹每個節點的左子樹和右子樹的高度差超過1的時候，就需要通過旋轉節點來維持平衡！旋轉又分為左旋、右旋、雙旋轉。

啥？雙旋轉？是的，顧名思義，在一些新增節點的情況下旋轉一次是不能達到平衡的，需要進行第二次旋轉，

五、平衡二叉樹插入節點的四種情況

當新節點插入後，有可能會有導致樹不平衡，而可能出現的情況就有4種，分別稱作左左，左右，右左，右右。

==而所謂的“左”和“右”無非就是代表新節點所插入的位置是左還是右！==

第一個左右代表位於根節點的左或者右，
第二個左右代表位於 【最接近插入節點的擁有兩個子節點的父節點】 位置的左或者右

==當然針對於第二個左右是我個人的見解，不一定完全正確。有自己想法的讀者，歡迎留言指正！==

下面以左左為例，分析一波：


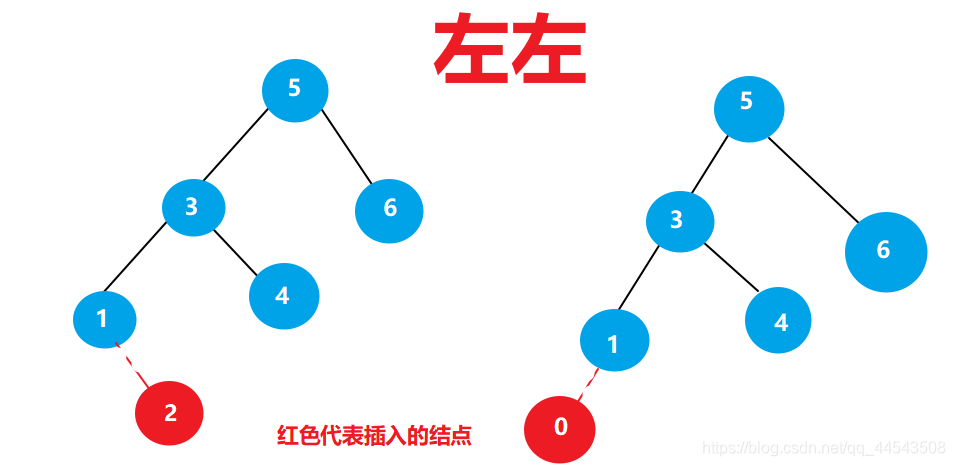
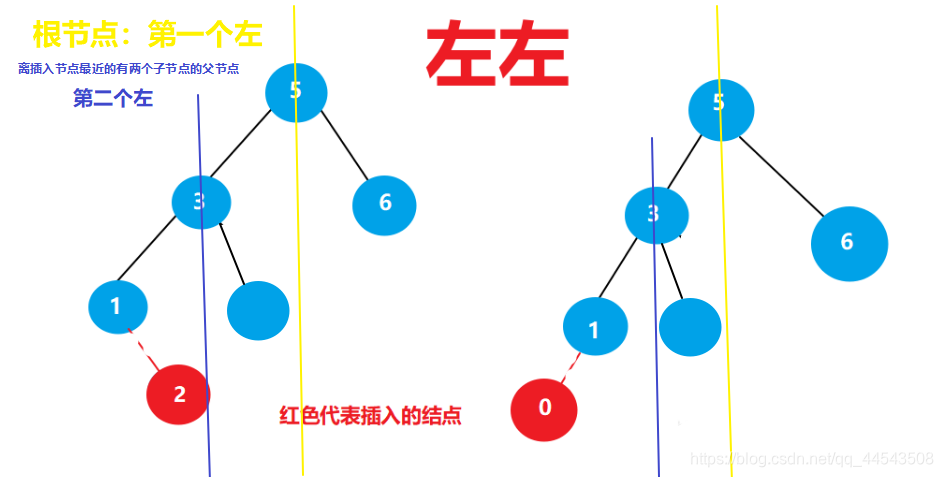
其中要特別注意的是：

右右、左左只需要旋轉一次就可以平衡。
左右、右左要旋轉兩次才能把樹調整平衡！

==其中旋轉的條件就是：當二叉排序樹每個節點的左子樹和右子樹的高度差超過1的時候！==

六、平衡二叉樹操作的程式碼實現

// 建立AVLTree
class AVLTree {
    private Node root;

    public Node getRoot() {
        return root;
    }

    // 查詢要刪除的結點
    public Node search(int value) {
        if (root == null) {
            return null;
        } else {
            return root.search(value);
        }
    }

    // 查詢父結點
    public Node searchParent(int value) {
        if (root == null) {
            return null;
        } else {
            return root.searchParent(value);
        }
    }

    // 編寫方法:
    // 1. 返回的 以node 為根結點的二叉排序樹的最小結點的值
    // 2. 刪除node 為根結點的二叉排序樹的最小結點
    /**
     *
     * @param node 傳入的結點(當做二叉排序樹的根結點)
     *            
     * @return 返回的 以node 為根結點的二叉排序樹的最小結點的值
     */
    public int delRightTreeMin(Node node) {
        Node target = node;
        // 迴圈的查詢左子節點，就會找到最小值
        while (target.left != null) {
            target = target.left;
        }
        // 這時 target就指向了最小結點
        // 刪除最小結點
        delNode(target.value);
        return target.value;
    }

    // 刪除結點
    public void delNode(int value) {
        if (root == null) {
            return;
        } else {
            // 1.需求先去找到要刪除的結點 targetNode
            Node targetNode = search(value);
            // 如果沒有找到要刪除的結點
            if (targetNode == null) {
                return;
            }
            // 如果我們發現當前這顆二叉排序樹只有一個結點
            if (root.left == null && root.right == null) {
                root = null;
                return;
            }

            // 去找到targetNode的父結點
            Node parent = searchParent(value);
            // 如果要刪除的結點是葉子結點
            if (targetNode.left == null && targetNode.right == null) {
                // 判斷targetNode 是父結點的左子結點，還是右子結點
                if (parent.left != null && parent.left.value == value) { // 是左子結點
                    parent.left = null;
                } else if (parent.right != null && parent.right.value == value) {// 是由子結點
                    parent.right = null;
                }
            } else if (targetNode.left != null && targetNode.right != null) { // 刪除有兩顆子樹的節點
                int minVal = delRightTreeMin(targetNode.right);
                targetNode.value = minVal;

            } else { // 刪除只有一顆子樹的結點
                // 如果要刪除的結點有左子結點
                if (targetNode.left != null) {
                    if (parent != null) {
                        // 如果 targetNode 是 parent 的左子結點
                        if (parent.left.value == value) {
                            parent.left = targetNode.left;
                        } else { // targetNode 是 parent 的右子結點
                            parent.right = targetNode.left;
                        }
                    } else {
                        root = targetNode.left;
                    }
                } else { // 如果要刪除的結點有右子結點
                    if (parent != null) {
                        // 如果 targetNode 是 parent 的左子結點
                        if (parent.left.value == value) {
                            parent.left = targetNode.right;
                        } else { // 如果 targetNode 是 parent 的右子結點
                            parent.right = targetNode.right;
                        }
                    } else {
                        root = targetNode.right;
                    }
                }

            }

        }
    }

    // 新增結點的方法
    public void add(Node node) {
        if (root == null) {
            root = node;// 如果root為空則直接讓root指向node
        } else {
            root.add(node);
        }
    }

    // 中序遍歷
    public void infixOrder() {
        if (root != null) {
            root.infixOrder();
        } else {
            System.out.println("二叉排序樹為空，不能遍歷");
        }
    }
}

// 建立Node結點
class Node {
    int value;
    Node left;
    Node right;

    public Node(int value) {

        this.value = value;
    }

    // 返回左子樹的高度
    public int leftHeight() {
        if (left == null) {
            return 0;
        }
        return left.height();
    }

    // 返回右子樹的高度
    public int rightHeight() {
        if (right == null) {
            return 0;
        }
        return right.height();
    }

    // 返回 以該結點為根結點的樹的高度
    public int height() {
        return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
    }

    //左旋轉方法
    private void leftRotate() {

        //建立新的結點，以當前根結點的值
        Node newNode = new Node(value);
        //把新的結點的左子樹設定成當前結點的左子樹
        newNode.left = left;
        //把新的結點的右子樹設定成帶你過去結點的右子樹的左子樹
        newNode.right = right.left;
        //把當前結點的值替換成右子結點的值
        value = right.value;
        //把當前結點的右子樹設定成當前結點右子樹的右子樹
        right = right.right;
        //把當前結點的左子樹(左子結點)設定成新的結點
        left = newNode;


    }

    //右旋轉
    private void rightRotate() {
        Node newNode = new Node(value);
        newNode.right = right;
        newNode.left = left.right;
        value = left.value;
        left = left.left;
        right = newNode;
    }

    // 查詢要刪除的結點
    /**
     *
     * @param value
     *            希望刪除的結點的值
     * @return 如果找到返回該結點，否則返回null
     */
    public Node search(int value) {
        if (value == this.value) { // 找到就是該結點
            return this;
        } else if (value < this.value) {// 如果查詢的值小於當前結點，向左子樹遞迴查詢
            // 如果左子結點為空
            if (this.left == null) {
                return null;
            }
            return this.left.search(value);
        } else { // 如果查詢的值不小於當前結點，向右子樹遞迴查詢
            if (this.right == null) {
                return null;
            }
            return this.right.search(value);
        }

    }

    // 查詢要刪除結點的父結點
    /**
     *
     * @param value 要找到的結點的值
     *            
     * @return 返回的是要刪除的結點的父結點，如果沒有就返回null
     */
    public Node searchParent(int value) {
        // 如果當前結點就是要刪除的結點的父結點，就返回
        if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
            return this;
        } else {
            // 如果查詢的值小於當前結點的值, 並且當前結點的左子結點不為空
            if (value < this.value && this.left != null) {
                return this.left.searchParent(value); // 向左子樹遞迴查詢
            } else if (value >= this.value && this.right != null) {
                return this.right.searchParent(value); // 向右子樹遞迴查詢
            } else {
                return null; // 沒有找到父結點
            }
        }

    }

    @Override
    public String toString() {
        return "Node [value=" + value + "]";
    }

    // 新增結點的方法
    // 遞迴的形式新增結點，注意需要滿足二叉排序樹的要求
    public void add(Node node) {
        if (node == null) {
            return;
        }

        // 判斷傳入的結點的值，和當前子樹的根結點的值關係
        if (node.value < this.value) {
            // 如果當前結點左子結點為null
            if (this.left == null) {
                this.left = node;
            } else {
                // 遞迴的向左子樹新增
                this.left.add(node);
            }
        } else { // 新增的結點的值大於 當前結點的值
            if (this.right == null) {
                this.right = node;
            } else {
                // 遞迴的向右子樹新增
                this.right.add(node);
            }

        }

        //當新增完一個結點後，如果: (右子樹的高度-左子樹的高度) > 1 , 左旋轉
        if(rightHeight() - leftHeight() > 1) {
            //如果它的右子樹的左子樹的高度大於它的右子樹的右子樹的高度
            if(right != null && right.leftHeight() > right.rightHeight()) {
                //先對右子結點進行右旋轉
                right.rightRotate();
                //然後在對當前結點進行左旋轉
                leftRotate(); //左旋轉..
            } else {
                //直接進行左旋轉即可
                leftRotate();
            }
            return ; //必須要!!!
        }

        //當新增完一個結點後，如果 (左子樹的高度 - 右子樹的高度) > 1, 右旋轉
        if(leftHeight() - rightHeight() > 1) {
            //如果它的左子樹的右子樹高度大於它的左子樹的高度
            if(left != null && left.rightHeight() > left.leftHeight()) {
                //先對當前結點的左結點(左子樹)->左旋轉
                left.leftRotate();
                //再對當前結點進行右旋轉
                rightRotate();
            } else {
                //直接進行右旋轉即可
                rightRotate();
            }
        }
    }

    // 中序遍歷
    public void infixOrder() {
        if (this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right != null) {
            this.right.infixOrder();
        }
    }

}

public class AVLTreeDemo {

    public static void main(String[] args) {      
        int[] arr = { 14, 21, 7, 3, 8, 9 };//任意測試節點陣列
        //建立一個 AVLTree物件
        AVLTree avlTree = new AVLTree();
        //新增結點
        for(int i=0; i < arr.length; i++) {
            avlTree.add(new Node(arr[i]));
        }

        //遍歷
        System.out.println("中序遍歷");
        avlTree.infixOrder();

        System.out.println("平衡處理...");
        System.out.println("樹的高度=" + avlTree.getRoot().height()); 
        System.out.println("樹的左子樹高度=" + avlTree.getRoot().leftHeight()); 
        System.out.println("樹的右子樹高度=" + avlTree.getRoot().rightHeight());
        System.out.println("當前的根結點=" + avlTree.getRoot());
    }
}

七、AVL樹總結

1、平衡二叉樹又稱AVL樹。

2、平衡二叉樹查詢、插入、刪除的時間複雜度都是 O(logN) 。

3、插入節點失去平衡的情況有4種，左左，左右，右左，右右。

4、右右、左左只需要旋轉一次就可以平衡，而左右、右左要旋轉兩次才能把樹調整平衡！

5、失去平衡最多也只要旋轉2次，所以，調整平衡的過程的時間複雜度為O(1)。

雖然平衡二叉樹有效的解決了極端類似蛇皮單鏈表的情況，但是平衡二叉樹也不是完美的，AVL樹最大的缺點就是刪除節點時有可能因為失衡，導致需要從刪除節點的父節點開始，不斷的回溯到根節點，如果這棵AVL樹很高的話，那中間就要判斷很多個節點，效率就顯然變的低下！因此我們後面將要學習2-3樹以及紅-黑樹，抽空寫嘍....

如果本文對你有一點點幫助，那麼請點個讚唄，你的贊同是我最大的動力，謝謝~

最後，若有不足或者不正之處，歡迎指正批評，感激不盡！如果有疑問歡迎留言，絕對第一時間回覆！

歡迎各位關注我的公眾號，裡面有一些java學習資料和一大波java電子書籍，比如說周志明老師的深入java虛擬機器、java程式設計思想、核心技術卷、大話設計模式、java併發程式設計實戰.....都是java的聖經，不說了快上Tomcat車，咋們走！最主要的是一起探討技術，嚮往技術，追求技術，說好了來了就是盆友喔...

相關推薦