目錄

• 1.簡介
• 2.從統計語言模型開始
  • 2.1序列概率模型
  • 2.2 N元統計模型
• 3.深度序列模型
  • 3.1神經概率模型
  • 3.2 one-hot向量表示法
  • 3.3 word2vec
  • 3.4word2vec的實際運用
• 4.總結
• 參考資料

1.簡介

word2vec是Google於2013年推出的開源的獲取詞向量word2vec的工具包。它包括了一組用於word embedding的模型，這些模型通常都是用淺層（兩層）神經網路訓練詞向量。

Word2vec的模型以大規模語料庫作為輸入，通過神經網路訓練到一個向量空間（通常為幾百維）。詞典中的每個詞都對應了向量空間中的一個獨一的向量，而且語料庫中擁有共同上下文的詞對映到向量空間中的距離會更近，並且其餘弦相似度較高。

在學習word2vec的過程中深受[4],[6]兩篇文章啟發，其中的背景資訊也借鑑了這些文章。並且學習序列生成模型中也從復旦邱錫鵬老師的《神經網路與深度學習》一書[8]中受益匪淺。

2.從統計語言模型開始

在機器學習中，統計語言模型(Statistic Language Model)作為自然語言處理的主要方法，也是很重要的一環。

在認知心理學中，有一個經典的實驗，當一個人看到下面兩個句子

麵包上塗黃油
麵包上塗襪子

後一個句子在人腦的語義整合時需要更多處理時間，更不符合自然語言規則。從統計的角度來看，這些語言規則可以看作時一種概率分佈，而對於以上的兩個句子，明顯後面的句子發生的概率更小。
一個長度為$T$的文字序列看作一個隨機事件$X_{(1:T)} = ⟨X_1, · · · ,X_T ⟩$，其中每個位置上的變數$X_t$ 的樣本空間為一個給定的詞表（vocabulary）$V$，整個序列$x_{1:T}$ 的樣本空間為$|V|^T$ 。
即，給定一個序列樣本給定一個序列樣本$x_{1:T} = x_1, x_2, · · · , x_T$ ，其概率可以看出是$T$個詞的聯合概率。

$$
P(X_{1:T} = x_{1_T}) = P(X_1 = x_1, X_2 = x_2, ... , X_T = x_T) = p(x_{1:T}).
$$

2.1序列概率模型

序列資料有兩個特點：（1）樣本是變長的；（2）樣本空間為非常大。對於一個長度為$T$ 的序列，其樣本空間為$|V|^T$ 。因此，我們很難用已知的概率模型來直接建模整個序列的概率。

根據概率的乘法公式，序列$x_{1:T}$ 的概率可以寫為

$$
p(x_{1:T}) = p(x_1)p(x_2|x_1)p(x_3|x_2) \cdots p(x_T|x_{1:(T-1)}) \
= \prod^T_{t=1} p(x_t|x_{1:(t-1)})
$$

其中$x_t ∈ V, t ∈ {1, · · · , T}$為詞表$V$ 中的一個詞，$p(x_1|x_0) = p(x_1)$。

因此，序列資料的概率密度估計問題可以轉換為單變數的條件概率估計問題，即給定$x_{1:(t−1)}$ 時$x_t$ 的條件概率$p(x_t|x_{1:(t−1)})$。

給定$N$ 個序列資料${x^{(n)}{1:T_n}}^N {n=1}$，序列概率模型需要學習一個模型$p_θ( {\mathbf x}|x_{1:(t−1)})$來最大化整個資料集的對數似然函式。

$$
{\mathop {max}{\theta}} \sum^N{n=1}log p_\theta(x^{(n)}{1:T_n}) = {\mathop {max}{\theta}}\sum^N_{n=1}\sum^T_{t=1}log p (x_t^{(n)}|x1^{(n)}_{1:(t-1)}).
$$

2.2 N元統計模型

由於資料稀疏問題，當$t$比較大時，依然很難估計條件概率$p(x_t|x_{1:(t−1)})$。一個簡化的方法是$N$元模型（N-Gram Model），假設每個詞$x_t$ 只依賴於其前面的
$n − 1$ 個詞（$n$階馬爾可夫性質），即

$$
p(x_t|x_{1:(t-1)}) = p(x_t|x_{(t-n+1):(t-1)}).
$$

當$n = 1$時，稱為一元（unigram）模型；當$n = 2$時，稱為二元（bigram）模型，以此類推。

一元模型：在一元模型中，$n=1$，即序列$x_{1:T}$每一個詞與其他詞獨立，即與它的上下文無關。即每個詞都是從多項概率分佈中獲得的，其對數似然函式為：

$$
log\prod^{N'}{n=1}p(x{1:T_n}^{(n)};\theta) = log \prod^{|V|}_{k=1}\theta^{m_k}k \
= \sum ^{|V|}{k=1}m_k log\theta_k
$$

其中，通過一定的公式證明，可以得出最大似然估計等價於頻率估計。

N元模型：與一元模型同理，當前詞只依賴於前$n-1$個詞，滿足$n$階馬爾可夫性質。通過最大似然函式可得：

$$
p(x_t|x_{(t-n+1):(t-1)}) = \frac {m(x_{(t-n+1):t})} {m(x_{(t-n+1):t-1})}
$$
其中${m(x_{(t-n+1):t})}$為$x_{(t-n+1):t}$在資料集上出現的次數。

平滑技術

考慮到以下兩個問題

1. 若一個詞$w$在當前語料庫（訓練集）中出現的次數為$0$，是否可以認為當前詞在語言序列中出現的概率為$0$？
2. 若一個詞$w1$與另一個詞$w2$在語料庫中出現的次數相同，是否可以人為該兩個詞在一定序列中出現的概率即$p(w_k|w_1^{k-1})$等於1？

當然以上兩個問題顯然是不能的，哪怕當前的訓練集多大，都無法避免的出現某些詞有著以上的兩種問題，因此，平滑化技術就是用於處理以上兩個問題。

3.深度序列模型

深度序列模型是指利用神經網路模型來估計$p_\theta(x_t|x_{1:(t-1)})$。

3.1神經概率模型

神經概率模型是由Bengio等人在文《A neural probabilistic language model. Journal of Machine Learning Research》(2003)中提出。該模型使用了一個重要的工具——詞向量。
神經語言概率模型一般可以分成三個部分：嵌入層、特徵層、輸出層。

3.1.1嵌入層

令$h_t = x_{1:(t−1)}$ 表示輸入的歷史資訊，一般為符號序列。由於神經網路模型一般要求輸入形式為實數向量，因此為了能夠使得神經網路模型能處理符號資料，需要將這些符號轉換為向量形式。一種簡單的轉換方法是通過一個嵌入表（Embedding Lookup Table）來將每個符號直接對映成向量表示。嵌入表也稱為嵌入矩陣或查詢表。

3.1.2特徵層

特徵層用於從輸入向量序列$e_1, · · · , e_{t−1}$ 中提取特徵，輸出為一個可以表示歷史資訊的向量$h_t$。簡單而言是通過訓練資料選取詞向量輸入到神經網路中進行計算。

特徵層可以通過不同型別的神經網路來實現，比如前饋神經網路和迴圈神經網路。常見的網路型別有以下三種：

1. 簡單平均。
2. 前饋神經網路。
3. 迴圈神經網路。

3.1.3輸出層

輸出層為一般使用softmax 分類器，接受歷史資訊的向量表示$h_t ∈ R^{d2}$，輸出為詞表中每個詞的後驗概率，輸出大小為$|V|$。簡而言之就是通常神經網路中的softmax，最後輸出概率分佈，然後可以進行loss的計算。

3.2 one-hot向量表示法

在谷歌提出word2vec模型之前，在語言神經網路模型中通常使用的是one-hot向量，即對於一個長度為10000的單詞語料庫，使用one-hot向量表示的話，單個單詞可以表示為10000*1的向量，若當前詞處於語料庫的第4096個位置，則當前單詞的one-hot向量是在第4096位置為1，其餘位置為0的10000*1的向量。

這種詞向量表示方法的優點是簡便，便於直接使用，因為文字無法之間在數學計算中使用，因此通過一種向量表示法，可以將其放入語言計算模型中使用。
但缺點很明顯，這種詞向量僅僅只能表示當前詞在語料庫中的位置，僅能表示其身份資訊，而無法表示兩個向量之間的關聯資訊。

因此需要用到一種能夠表示兩個詞之間相關資訊的向量表示法。

3.3 word2vec

word2vec又可稱為word embedding，即詞嵌入，因為無論是word2vec還是one-hot，這兩種詞的表示方法都是在神經概率模型中的嵌入層使用，作為神經網路模型能夠處理的符號資料使用。

word2vec的表示形式與one-hot不同，每一個詞在word2vec中同樣是一個向量，但該向量的長度不固定，即非語料庫的長度，該長度m可有演算法的使用者而定，而向量的每個維度也並非直接使用0或1這種簡單的方式表示，一般是任意的實數。由此表示形式，可以得出，這種詞的表示方法既可以表示當前詞的身份資訊（即區別於其他詞），又可以計算當前詞與其他詞之間的語義上的關係。

我們可以思考一下這種詞之間的語義關聯性。首先，對於每一個詞而言，因其是多維向量，因此可以對映到高維空間中。其次，在對映到高維空間後，可以聯絡向量之間的關係，通過計算兩個向量之間的餘弦值而得出兩個向量之間的關聯程度。更甚之，可以通過詞向量之間的加減，計算出其他詞。

對於如何獲取詞向量而言，對於神經概率模型中，詞向量（word embedding）即為神經網路中的引數，因其作為嵌入層的引數，輸入形式為實數向量。因此獲取word embedding，即是神經網路中的引數的學習。

這種訓練通過給定一個訓練序列資料集，而神經網路模型的訓練目標則是為找到一組引數$\theta$，使得對數似然函式最大。其中$\theta$表示網路中的所有引數，包括嵌入矩陣M以及神經網路的權重和偏置。
而該嵌入矩陣即為詞向量的矩陣，其大小為$M\times N$，$N$為語料庫詞的數量，M為給定的詞向量的長度。

3.3.1 word2vec訓練的神經網路模型

在google於2013年所提出的兩篇文章[2]與[3]中，使用了兩種重要的模型——CBOW模型與Skip-Gram模型。

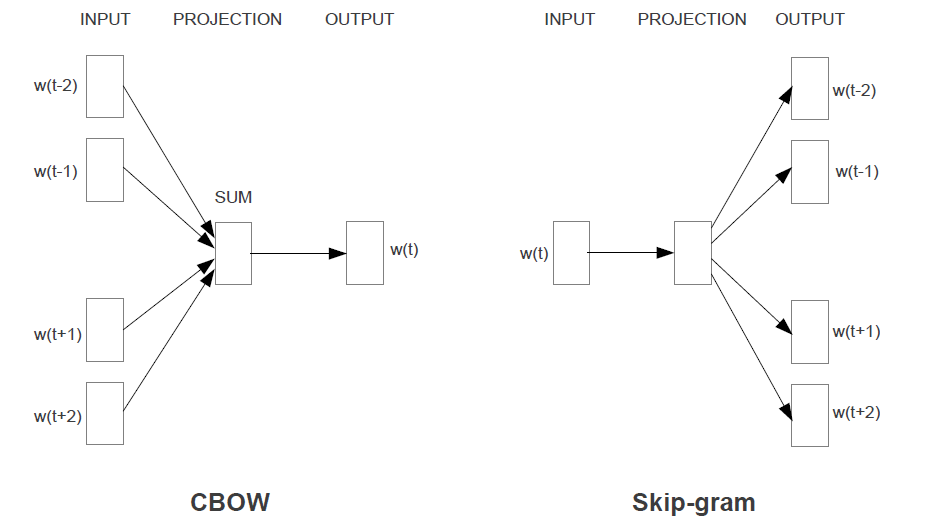
跳字模型(Skip-gram)

由論文中所給出的圖，可以形象地得知對於skip-gram模型而言，是由當前的詞生成周圍的詞的一種神經概率模型，在這些模型討論中，一般將詞分為兩種（最後訓練出來的詞向量也分為這兩種），一種是作為中心詞，另一種則是作為背景詞。
這種假設方式在skip-gram模型中可以很明確的看出，由中心詞（圖中為$w(t)$）經過神經概率模型生成周圍的詞$(w(t-2), w(t-1), w(t+1), w(t+2))$，在這之中，生成周圍的詞有前後各兩個，相應的，把這個生成背景詞範圍的大小叫做背景詞視窗，圖中的背景詞視窗為2。

在以上模型中，我們不妨將中心詞的詞向量設為$v_c$，而背景詞可認為是$u_o$。在skip-gram模型中，輸入層獲取到當前作為中心詞的向量，並在預測層與模型引數（實為背景詞的詞向量）做乘積計算，最後在輸出層做一個softmax的運算輸出生成背景詞的一個概率分佈。

設中心詞$w_c$在詞典中索引為$c$，背景詞$w_o$在詞典中索引為$o$，給定中心詞生成背景詞的條件概率可以通過對向量內積做softmax運算而得到：

$$
P(w_o \mid w_c) = \frac{\text{exp}(\boldsymbol{u}_o^\top \boldsymbol{v}c)}{ \sum{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}.
$$

其中詞典索引集$\mathcal{V} = {0, 1, \ldots, |\mathcal{V}|-1}$。假設給定一個長度為$T$的文字序列，設時間步$t$的詞為$w^{(t)}$。假設給定中心詞的情況下背景詞的生成相互獨立，當背景視窗大小為$m$時，跳字模型的似然函式即給定任一中心詞生成所有背景詞的概率

$$
\prod_{t=1}^{T} \prod_{-m \leq j \leq m, j \neq 0} P(w^{(t+j)} \mid w^{(t)})
$$

訓練跳字模型

在上文中已經提到整個跳字模型從輸入層到輸出層的一個計算，那麼對於這個神經網路，使用反向傳播便可以對整個模型與詞向量做一個訓練。而在3.1.3小節及之後的討論中提到，訓練中是通過最大化似然函式來學習模型引數，即最大似然估計。由上文的推導即分析，可以得出loss為：

$$ - \sum_{t=1}^{T} \sum_{-m \leq j \leq m, j \neq 0} \text{log}, P(w^{(t+j)} \mid w^{(t)}).$$

如果使用隨機梯度下降，那麼在每一次迭代裡我們隨機取樣一個較短的子序列來計算有關該子序列的損失，然後計算梯度來更新模型引數。梯度計算的關鍵是條件概率的對數有關中心詞向量和背景詞向量的梯度。根據定義，首先看到

$$\log P(w_o \mid w_c) =
\boldsymbol{u}_o^\top \boldsymbol{v}c - \log\left(\sum{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)\right)$$

通過微分，我們可以得到上式中$\boldsymbol{v}_c$的梯度

$$
\begin{aligned}
\frac{\partial \text{log}, P(w_o \mid w_c)}{\partial \boldsymbol{v}_c}
&= \boldsymbol{u}o - \frac{\sum{j \in \mathcal{V}} \exp(\boldsymbol{u}_j^\top \boldsymbol{v}_c)\boldsymbol{u}j}{\sum{i \in \mathcal{V}} \exp(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\
&= \boldsymbol{u}o - \sum{j \in \mathcal{V}} \left(\frac{\text{exp}(\boldsymbol{u}_j^\top \boldsymbol{v}c)}{ \sum{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}\right) \boldsymbol{u}_j\
&= \boldsymbol{u}o - \sum{j \in \mathcal{V}} P(w_j \mid w_c) \boldsymbol{u}_j.
\end{aligned}
$$

它的計算需要詞典中所有詞以$w_c$為中心詞的條件概率。有關其他詞向量的梯度同理可得。

訓練結束後，對於詞典中的任一索引為$i$的詞，我們均得到該詞作為中心詞和背景詞的兩組詞向量$\boldsymbol{v}_i$和$\boldsymbol{u}_i$。在自然語言處理應用中，一般使用跳字模型的中心詞向量作為詞的表徵向量。

以上這一段公式的推導是取自《dive into deeplearning》一書[7]中，其中更為詳細的推導可以見[4]，這篇文章中有著對整個word2vec模型與公式上更為詳細與嚴謹的推導過程。

連續詞袋模型（CBOW）

CBOW模型（Continuous Bag-of-Words Model）與skip-gram模型相反，CBOW模型是由周圍的詞（即背景詞）生成中心詞的一種神經概率模型，這裡我們將背景詞記為$v_o$，生成的中心詞記為$u_c$。由於是多個背景詞生成中心詞，因此在輸入層中，對背景詞的詞向量選取並進行求和取平均數，然後與跳字模型相同，通過與中心詞的向量做乘積運算（即在隱藏層和輸出層之間做矩陣運算），以及在輸出層上的softmax歸一化運算。

設中心詞$w_c$在詞典中索引為$c$，背景詞$w_{o_1}, \ldots, w_{o_{2m}}$在詞典中索引為$o_1, \ldots, o_{2m}$，那麼給定背景詞生成中心詞的條件概率

$$P(w_c \mid w_{o_1}, \ldots, w_{o_{2m}}) = \frac{\text{exp}\left(\frac{1}{2m}\boldsymbol{u}c^\top (\boldsymbol{v}{o_1} + \ldots + \boldsymbol{v}{o{2m}}) \right)}{ \sum_{i \in \mathcal{V}} \text{exp}\left(\frac{1}{2m}\boldsymbol{u}i^\top (\boldsymbol{v}{o_1} + \ldots + \boldsymbol{v}{o{2m}}) \right)}.$$
為了讓符號更加簡單，我們記$\mathcal{W}o= {w{o_1}, \ldots, w_{o_{2m}}}$，且$\bar{\boldsymbol{v}}o = \left(\boldsymbol{v}{o_1} + \ldots + \boldsymbol{v}{o{2m}} \right)/(2m)$，那麼上式可以簡寫成

$$P(w_c \mid \mathcal{W}_o) = \frac{\exp\left(\boldsymbol{u}_c^\top \bar{\boldsymbol{v}}o\right)}{\sum{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)}.$$

給定一個長度為$T$的文字序列，設時間步$t$的詞為$w^{(t)}$，背景視窗大小為$m$。連續詞袋模型的似然函式是由背景詞生成任一中心詞的概率

$$ \prod_{t=1}^{T} P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)}).$$

訓練連續詞袋模型

同樣對於CBOW模型的訓練與skip-gram模型類似，通過最大似然估計等價於最小化損失函式，可以得到$loss$：

$$ -\sum_{t=1}^T \text{log}, P(w^{(t)} \mid w^{(t-m)}, \ldots, w^{(t-1)}, w^{(t+1)}, \ldots, w^{(t+m)}).$$
注意到

$$\log,P(w_c \mid \mathcal{W}_o) = \boldsymbol{u}_c^\top \bar{\boldsymbol{v}}o - \log,\left(\sum{i \in \mathcal{V}} \exp\left(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o\right)\right).$$

通過微分，我們可以計算出上式中條件概率的對數有關任一背景詞向量$\boldsymbol{v}_{o_i}$（$i = 1, \ldots, 2m$）的梯度

$$\frac{\partial \log, P(w_c \mid \mathcal{W}o)}{\partial \boldsymbol{v}{o_i}} = \frac{1}{2m} \left(\boldsymbol{u}c - \sum{j \in \mathcal{V}} \frac{\exp(\boldsymbol{u}_j^\top \bar{\boldsymbol{v}}_o)\boldsymbol{u}j}{ \sum{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \bar{\boldsymbol{v}}_o)} \right) = \frac{1}{2m}\left(\boldsymbol{u}c - \sum{j \in \mathcal{V}} P(w_j \mid \mathcal{W}_o) \boldsymbol{u}_j \right).$$

有關其他詞向量的梯度同理可得。同跳字模型不一樣的一點在於，我們一般使用連續詞袋模型的背景詞向量作為詞的表徵向量。

這一部分的梯度推導也取自於《dive into deeplearning》一書[7]中。

3.3.2近似計算

在3.3.1節中，可以由兩種模型的條件概率看出，對於一個詞的條件概率而言，背景視窗雖然能夠限制背景詞的數量，但是這個背景詞需要從整個語料庫中選擇，即對於跳字模型中的條件概率而言：

$$
P(w_o \mid w_c) = \frac{\text{exp}(\boldsymbol{u}_o^\top \boldsymbol{v}c)}{ \sum{i \in \mathcal{V}} \text{exp}(\boldsymbol{u}_i^\top \boldsymbol{v}_c)}.
$$
其中的分母的$u_i$需要從訓練集的語料庫中選擇，因此使得最終的softmax的計算量非常的巨大，因此提出了兩種近似計算，分別是Hierarchical softmax(層序softmax)與Negative Sampling(負取樣)。我對這兩種方法深受[4]這篇文章的理解，因此接用其中的表示方法。

層序softmax

在一般書籍與論文的舉例中，通過使用平衡樹來解釋，但在實際實現的程式碼中則是通過Huffman樹去實現這個方法。

文章[4]中引入相關的表示記號如下：

1. $p^w$：從根節點出發到達w對應葉子節點的路徑。
2. $l^w$：路徑$p^w$中包含節點的個數。
3. $p^w_1, p^w_2, \cdots, p^w_{l^w}$：路徑$p^w$中的$l^w$個結點，其中$p^w_1$表示根結點，$p^w_{l^w}$表示詞w對應的結點。
4. $d^w_1, d^w_2, \cdots, d^w_{l^w} \in {0, 1}$：詞w的Huffman編碼，它由$l^w - 1$位編碼構成，$d^w_j$表示路徑$p^w$中第j個結點對應的編碼（根節點不對應編碼）。
5. $\theta^w_1, \theta^w_2, \cdots, \theta^w_{l^w-1} \in \mathbb{R}^m$：路徑$p^w$中非葉子結點對應的向量，$\theta^w_j$表示路徑$p^w$中第j個非葉子結點對應的向量。

由這些標記符號我們可以結合以下的二叉樹圖對整體引數的分佈記每個詞的條件概率做一個深入的理解。

其中，正如文章[4]中所提到的那樣，為何還要為Huffman樹中的每個非葉子結點也定義一個同長的向量呢？文章[4]中解釋道：“它們只是演算法中的輔助向量”。具體的詳細推導可見文章[4]，這裡給出一定簡要的理解與解釋。

首先是為什麼Huffman樹能夠大量的減少計算量。我們可以通過二叉樹形象的來看。

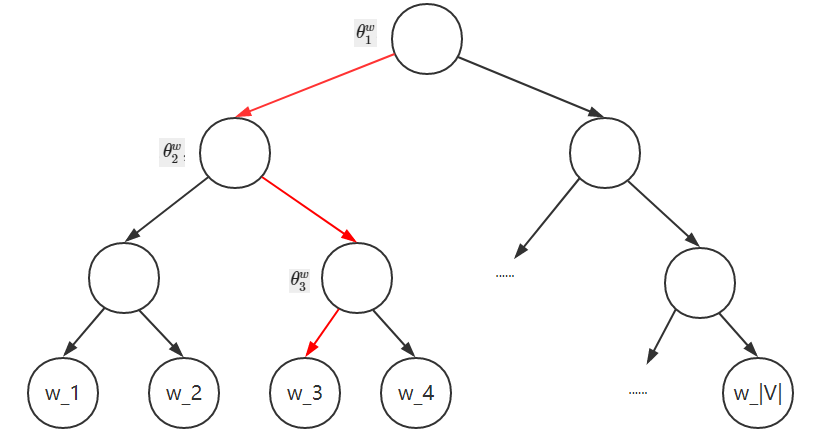
再上圖的二叉樹中，我們可以看到，語料庫大小為$|V|$的情況下，每個詞向量作為二叉樹的根節點的每個向量資料，其中由輔助引數$\theta^w_{l^w-1}$非葉子結點上的向量資料。那麼在二叉樹中如何定義條件概率函式$P(w_c \mid Context(w))$(其中使用CBOW模型的條件概率)？更具體的說，就是如何使用平衡二叉樹中的結點向量去定義這個條件概率函式。以圖中紅色的路徑為例，中間一共經歷了3次分支，每一次分支都可以視為二分類。
從二分類的角度來看，對於每一個非葉子結點，需要考慮為左右孩子制定一個分類類別，我們假設左為正，而右為負，根據邏輯迴歸，易知：

$$\sigma(x^T_w \theta) = \frac{1}{1+\exp(-x^T_w \theta)}.$$
那麼分類為負的概率則為：

$$
1 - \sigma(x^T_w \theta)
$$
其中$\theta$則是作為非葉子結點的輔助引數向量。

那麼，我們可以看到該路徑的條件概率則為（以下忽略引數）：

$$P(w_3 \mid Context(w)) = \sigma(\boldsymbol{x}w^\top \boldsymbol{\theta}{n(w_3,1)}) \cdot (1- \sigma(\boldsymbol{x}w^\top \boldsymbol{\theta}{n(w_3,2)})) \cdot \sigma(\boldsymbol{x}w^\top \boldsymbol{\theta}{n(w_3,3)}).$$

$$P(w_c \mid Context(w)) = \prod^{l^w}{j=2}p(d^w_j \mid x_w, \theta^w{j-1}),$$
其中

$$
p(d^w_j \mid x_w, \theta^w_{j-1}) =
\begin{cases}
\sigma(x^T_w \theta^w_{j-1}), & d^w_j = 1 \
1 - \sigma(x^T_w \theta^w_{j-1}), & d^w_j = 0
\end{cases}
$$

或寫成整體表達式：

$$
p(d^w_j \mid x_w, \theta^w_{j-1}) = [\sigma(x^T_w \theta^w_{j-1})]^{d^w_j} \cdot [1 - \sigma(x^T_w \theta^w_{j-1})]^{1-d^w_j}
$$

其中$d^w_j=1$表示為正類，$d^w_j=0$表示為負類。

也就是說，通過將語料庫中的每一個詞表示為二叉樹上的葉子結點，可以將原來的條件概率變為簡單的路徑上的二分類的相乘，由此大大的縮短了整個計算量。
那麼又為何使用Huffman樹呢？學過二叉樹與Huffman樹的同學到現在應該能夠想到，對於整個語料庫中，每一個詞的復現的頻率是不同的，因此在計算過程中，有一些高頻率的的詞用到的次數就較多，而Huffman樹則可以通過對高頻詞進行較短的編碼，對低頻詞進行較長的編碼來進一步縮短計算量。

負取樣

相比於層序softmax，負取樣顯得更為簡單。
負取樣同樣使用了正負樣本的概念，不再使用Huffman樹，而是利用隨機負取樣，如此能夠大幅提高效能。
同樣是在CBOW模型中，詞w的上下文為Context(w)需要預測w，那麼給定的Context(w)就是正樣本，而負樣本則是不出現在這個上下文視窗中的詞。

那麼，負樣本是如何選取的呢？在上一小節也提到，對於語料庫中的不同詞而言，不同的詞的復現頻率是不同的，因此在語料庫上的負樣本的選取就變成了一個帶權取樣問題。
而對於樣本的權值設定則是通過如下公式：

$$
p(w)=\frac{[count(w)]^{\frac{3}{4}}}{\sum_{u \in D}[count(u)]^{\frac{3}{4}}}
$$

在選取好一個關於w的負樣本子集NEG(w)，並且定義了詞典$D$中的任意詞$w'$，都有：

$$
L^w(w')=
\begin{cases}
1 & w'=w \
0 & w'\neq w
\end{cases}
$$

對於一個給定的正樣本$(Context(w),w)$，我們希望最大化

$$
g(w)=\prod_{u\in {w}\bigcup NEG(w)} p(u|Context(w))
$$

其中，正負樣本的條件概率類似於層序softmax中的正負類的條件概率：

$$
p(u|Context(w))=
\begin{cases}
\sigma(X_w^T\theta^u) & L^w(u)=1 \
1-\sigma(X_w^T\theta^u) & L^w(u)=0
\end{cases} \
= [\sigma(X_w^T\theta^u)]^{L^w(u)} \cdot [1-\sigma(X_w^T\theta^u)]^{1-L^w(u)}
$$

負取樣直接通過負樣本（取樣不出現在背景視窗中的詞）與正樣本（出現在背景視窗中的詞）計算目標詞出現的條件概率，相比於層序softmax，不需要構建一個Huffman樹與使用樹中每一個非葉子節點的引數向量，取而代之的是直接使用語料庫中的詞。

對於層序softmax與負取樣的梯度計算的詳細推導可以在文章[4]中有詳細提到。

詞向量的選取

對於層序softmax與負取樣這兩種近似計算訓練出來的詞向量，每一個詞其實有兩種形式的詞向量，一種是作為中心詞的詞向量，一種是作為背景詞的詞向量，一般情況下直接選擇中心詞的詞向量作為最終訓練得到的詞向量使用。可以從負取樣近似訓練中得出，作為背景詞的詞向量可能會是不存在生成目標詞的背景視窗中，因此作為背景詞的詞向量相比之下的置信度較低。

3.4word2vec的實際運用

詞向量的語言翻譯

在google的Tomas Mikolov團隊開發了一種詞典和術語表的自動生成技術，能夠把一種語言轉變成另一種語言，該技術利用資料探勘來構建兩種語言的結構模型，然後加以對比，每種語言詞語之間的關鍵即“語言空間”，可以被表徵成數學意義上的向量集合。在向量空間內，不同的語言享有許多共性，只有實現一個向量空間向另一個向量空間的對映與轉換，語言翻譯即可實現。該技術效果非常不錯，對英語和西班牙語的翻譯準確率高達90%。
文[5]在介紹演算法時舉了一個簡單的例子，可以幫助我們更好地理解詞向量的工作原理。

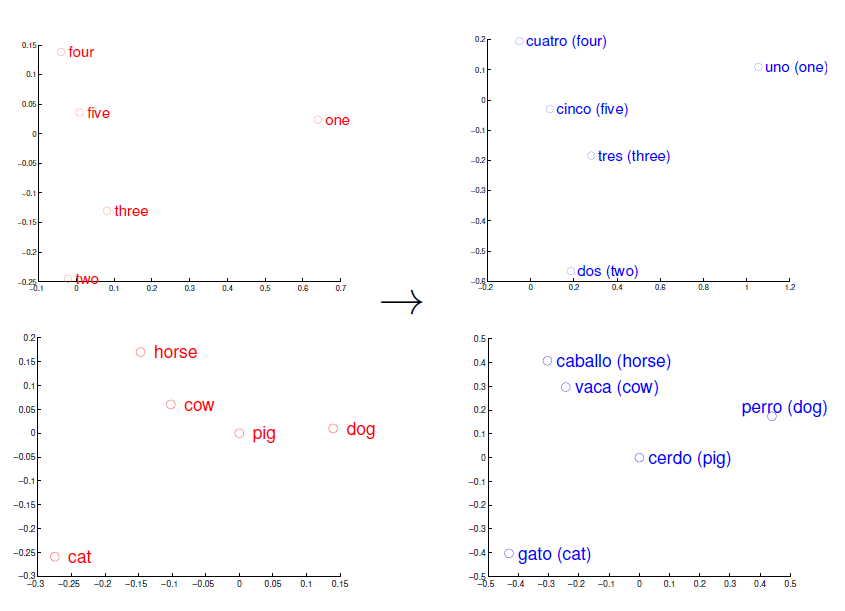
詞向量的近義詞與類比詞

詞向量的一個簡單應用就是求得當前次的近義詞與類比詞。

對於近義詞而言，直接在訓練好的詞向量中計算其他詞與當前次的餘弦相似度，選取最高的幾個即可求出當前次的近義詞。

除了求近義詞以外，我們還可以使用預訓練詞向量求詞與詞之間的類比關係。例如，“man”（男人）: “woman”（女人）:: “son”（兒子） : “daughter”（女兒）是一個類比例子：“man”之於“woman”相當於“son”之於“daughter”。求類比詞問題可以定義為：對於類比關係中的4個詞 $a : b :: c : d$，給定前3個詞$a$、$b$和$c$，求$d$。設詞$w$的詞向量為$\text{vec}(w)$。求類比詞的思路是，搜尋與$\text{vec}(c)+\text{vec}(b)-\text{vec}(a)$的結果向量最相似的詞向量。

又如“首都-國家”類比：“beijing”（北京）之於“china”（中國）相當於“tokyo”（東京）之於什麼？答案應該是“japan”（日本）。

通過詞向量之間的加減即可求得所對應詞的類比詞。

4.總結

本文中，簡要的對當前自然語言處理中所使用的詞向量做了一個簡要的介紹。在詞向量的訓練過程中，每一個詞向量（word vector）都被要求為相鄰上下文中的word的出現作預測，所以儘管我們是隨機初始化Word vectors，但是這些vectors最終仍然能通過上面的預測行為捕獲到word之間的語義關係，從而訓練到較好的word vectors。而這些訓練好的詞向量在一些自然語言任務中使用的效果非常出色，比如詞向量就可以應用到情感分類的問題中。

參考資料

[1] Yoshua Bengio, Réjean Ducharme, Pascal Vincent, Christian Jauvin. A Neural Probabilistic Language Model. Journal of machine learning(JMLR), 3:1137-1155, 2003
[2] Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[J]. arXiv preprint arXiv:1301.3781, 2013.
[3] Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]//Advances in neural information processing systems. 2013: 3111-3119.
[4] https://www.cnblogs.com/peghoty/p/3857839.html
[5] Tomas Mikolov, Quoc V. Le, llya Sutskever. Exploiting Similarities among Languages for Machine Translation. arXiv:1309.4168v1, 2013.
[6] https://www.zybuluo.com/Dounm/note/591752#5-%E5%9F%BA%E4%BA%8Enegative-sampling%E7%9A%84%E6%A8%A1%E5%9E%8B
[7] https://zh.d2l.ai/
[8] https://nndl.github