python實現直方圖均衡化,理想高通濾波與高斯低通濾波
寫在前面
HIT大三上學期視聽覺訊號處理課程中視覺部分的實驗二,經過和學長們實驗的對比發現每一級實驗要求都不一樣,因此這裡標明瞭是2019年秋季學期的視覺實驗二。
由於時間緊張,程式碼沒有進行任何優化,實驗演算法僅供參考。
實驗要求
實現影象直方圖均衡化,要求顯示均衡化前、後直方圖以及均衡化後圖像。
對單通道影象進行DFT變換,要求顯示幅度圖和相點陣圖,並設計理想高通濾波器和高斯低通濾波器對影象進行頻域濾波,並顯示濾波之後的影象。 注:除DFT和IDFT外,不允許調庫
實驗程式碼
程式碼首先貼在這裡,僅供參考
原始碼
首先是實現影象直方圖均衡化的程式碼
from ReadBmp import ReadBmp import matplotlib.pyplot as plt import numpy as np filename1 = "1.bmp" bmp = ReadBmp(filename1) bmp.gray() # 統計各畫素點數 h = np.array([0 for i in range(256)]) h1 = [] for pixel in bmp.data: h[pixel[0]] = h[pixel[0]] + 1 h1.append(pixel[0]) # 畫出原先的直方圖 plt.subplot(1,2,1) plt.hist(h1, bins = 256) # 歸一化 hs = h / len(bmp.data) # 計算累計分佈 hp = np.array([0.0 for i in range(256)]) for i in range(256): hp[i] = np.round(np.sum(hs[0:i+1]) * 255) T = hp.astype('uint8') # 建立新影象,並統計新影象的各個畫素點的個數 hn = np.array([0 for i in range(256)]) h2 = [] for pixel in bmp.data: s = T[pixel[0]] pixel[0] = s pixel[1] = s pixel[2] = s hn[pixel[0]] = hn[pixel[0]] + 1 h2.append(s) bmp.creataBmp("2.bmp") # 畫出新影象的直方圖 plt.subplot(1,2,2) plt.hist(h2, bins = 256) plt.show()
其中讀取bmp影象的程式是我自己寫的,這裡不再贅述(直接呼叫了實驗一寫好的bmp檔案讀取程式,具體程式碼見github)
然後是理想高通濾波和高斯低通濾波的程式
import numpy as np import cv2 import matplotlib.pyplot as plt def IdealHighPassFiltering(f_shift): # 設定濾波半徑 D0 = 8 # 初始化 m = f_shift.shape[0] n = f_shift.shape[1] h1 = np.zeros((m, n)) x0 = np.floor(m/2) y0 = np.floor(n/2) for i in range(m): for j in range(n): D = np.sqrt((i - x0)**2 + (j - y0)**2) if D >= D0: h1[i][j] = 1 result = np.multiply(f_shift, h1) return result def GaussLowPassFiltering(f_shift): # 設定濾波半徑 D0 = 8 # 初始化 m = f_shift.shape[0] n = f_shift.shape[1] h1 = np.zeros((m, n)) x0 = np.floor(m/2) y0 = np.floor(n/2) for i in range(m): for j in range(n): D = np.sqrt((i - x0)**2 + (j - y0)**2) h1[i][j] = np.exp((-1)*D**2/2/(D0**2)) result = np.multiply(f_shift, h1) return result img =cv2.imread('1.bmp',0) f=np.fft.fft2(img) f_shift=np.fft.fftshift(f) # 幅度圖 s= np.log(abs(f_shift)) # 相點陣圖 p= abs(np.angle(f_shift)) plt.subplot(2,2,1) plt.imshow(s, 'gray') plt.subplot(2,2,2) plt.imshow(p, 'gray') # 理想高通濾波 IHPF = IdealHighPassFiltering(f_shift) new_f1 = np.fft.ifftshift(IHPF) new_image1 = np.uint8(np.abs(np.fft.ifft2(new_f1))) plt.subplot(2,2,3) plt.imshow(new_image1, 'gray') # 高斯低通濾波 GLPF = GaussLowPassFiltering(f_shift) new_f2 = np.fft.ifftshift(GLPF) new_image2 = np.uint8(np.abs(np.fft.ifft2(new_f2))) plt.subplot(2,2,4) plt.imshow(new_image2, 'gray') plt.show()
實驗結果
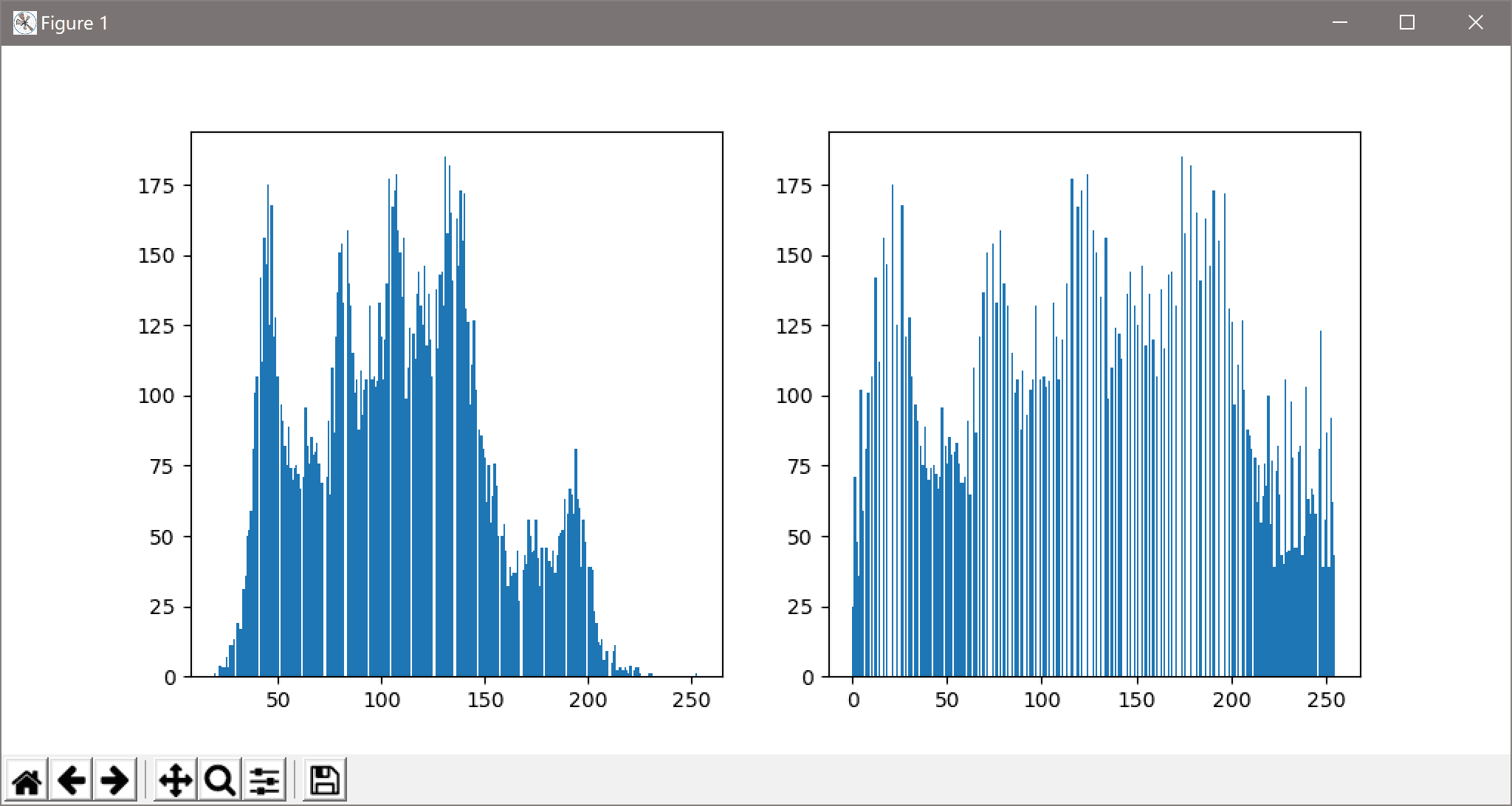
實驗結果的影象如下圖所示
這是直方圖均衡化的執行結果,其中左圖是做直方圖均衡化前對畫素統計的直方圖,右圖是做直方圖均衡化後對畫素統計的直方圖
這是畫出影象的幅度圖和相點陣圖,對影象做理想高通濾波和高斯低通濾波的結果,其中1是幅度圖,2是相點陣圖,3是理想高通濾波的結果,4是高斯低通濾波的結果

要點講解
關於實驗演算法的大致流程,已在程式中用註釋標明,這裡只記錄需要注意的地方
在直方圖均衡化中,要注意直方圖函式的用法,該函式可以對輸入的矩陣中的數值進行自動的分類,而不用手動分好之後再用直方圖函式去畫,之前沒有仔細看該函式的用法,導致找了好長時間沒找到問題。
關於直方圖均衡化的原理,需要一定的數學公式的推導,然而其結論十分簡單,只有一個公式,對理解公式推導無需求的直接拿公式來用就可以了。(即程式中的歸一化加計算累積分佈部分)
關於理想高通濾波和高斯低通濾波,可以看到其程式碼大體框架是一致的,只有中間if語句中的判斷條件不一樣,理解原理之後直接替換if語句即可。
最終畫出理想高通濾波的影象時,網上給出的一些執行結果可能和我們執行的不一致,類似於下圖中圖一的影象,原因在於這一句話中:
new_image1 = np.uint8(np.abs(np.fft.ifft2(new_f1))),注意到中間呼叫了np.abs()函式,由於經過DFT變換之後所得的數值是複數,而不是實數,若將np.abs()替換為np.real(),即只取其實部,則得到的是圖一,而使用np.abs(),得到的則是圖二。個人感覺圖二才是相對正確一些的結果,圖一相當於將虛部捨棄掉了,這是不太好的。
以下是圖一

以下是圖二

知識總結
關於直方圖均衡化的數學原理,我參考的是這篇部落格。直方圖均衡化的公式推導較為複雜,然而其結果卻十分簡單,因此在python中一個迴圈就實現了。
直方圖均衡化的數學原理
關於如何畫直方圖,參考的是這兩篇部落格
python之matplotlib.pyplot直方圖
關於相點陣圖和振幅圖的畫法,參考的是下面這兩篇部落格
python opencv dft
進行傅立葉變換,畫出幅值譜圖、相位譜圖以及實現位移後的幅值譜圖和相位譜圖
案例解釋影象傅立葉變換的幅度譜和相位譜的以及反變換
關於理想高通和高斯低通濾波器的實現,參考的是以下這幾篇部落格
理想高通濾波器
理想低通濾波器、Butterworth濾波器和高斯濾波器(matlab)
其中在理想高通和高斯低通濾波器中,需要用到矩陣乘法,關於幾種不同的矩陣乘法參考的是這篇部落格
numpy 三種矩陣乘法
實驗總結
很簡單的一個實驗,總時間加起來大致4個小時左右,做這麼快的主要原因是,本來同學來哈爾濱找我玩,正玩得開心,結果突然告訴我這個實驗要今天晚上交(之前以為這個實驗還有一週的ddl),所以潛能爆發,從三點寫到六點差不多就寫完
