非常完整的線性DP及記憶化搜尋講義
基礎概念
我們之前的課程當中接觸了最基礎的動態規劃。
動態規劃最重要的就是找到一個狀態和狀態轉移方程。
除此之外,動態規劃問題分析中還有一些重要性質,如:重疊子問題、最優子結構、無後效性等。
最優子結構 的概念:
1)如果問題的一個最優解包含了子問題的最優解,則該問題具有最優子結構。當一個問題具有最優子結構的時候,我們就可能要用到動態規劃(貪心策略也是有可能適用的)。
2)尋找最優子結構時,可以遵循一種共同的模式:
- 問題的一個解可以是一個選擇。例如,裝配站選擇問題。
- 假設對一個給定的問題,已知的是一個可以導致最優解的選擇。不必關心如何確定這個選擇,假定他是已知的。
- 在已知這個選擇之後,要確定那些子問題會隨之發生,以及如何最好的描述所的得到的子問題空間。
- 利用一種“剪貼”技術,來證明在問題的一個最優解中,使用的子問題的解本身也必須是最優的。
3)最優子結構在問題域中以兩種方式變化:
- 有多少個子問題被使用在原問題的一個最優解中,以及
- 在決定一個最優解中使用那些子問題時有多少個選擇
在裝配線排程問題中,一個最優解只使用了一個子問題,但是,為確定一個最優解,我們必須考慮兩種選擇。
4)動態規劃與貪心演算法的區別
- 動態規劃以自底向上的方式來利用最優子結構。也就是說,首先找到子問題的最優解,解決的子問題,然後找到問題的一個最優解。尋找問題的一個最優解需要首先在子問題中做出選擇,即選擇用哪一個來求解問題。問題解的代價通常是子問題的代價加上選擇本身帶來的開銷。
- 在貪心演算法中是以自頂向下的方式使用最優子結構。貪心演算法會先做選怎,在當時看來是最優的選擇,然後在求解一個結果子問題,而不是現尋找子問題的最優解,然後再做選擇。
重疊子問題 的概念:
適用於動態規劃求解的最優化問題必須具有的第二個要素是子問題的空間要“很小”,也就是用來解原問題的遞迴演算法可以反覆的解同樣的子問題,而不是總在產生新的子問題。
比如:狀態 \(i\) 的求解和狀態 \(i-1\) 有關,狀態 \(i-1\) 的求解和狀態 \(i-2\) 有關,那麼當我們計算得到狀態 \(i\) 的時候,我們就可以用 \(f[i]\) 來表示狀態 \(i\) ,那麼當我下一次需要用到狀態 \(i\) 的時候,我直接返回 \(f[i]\) 即可。
無後效性 的概念:
某階段的狀態一旦確定,則此後過程的演變不再受此前各種狀態及決策的影響,簡單的說,就是“未來與過去無關”,當前的狀態是此前歷史的一個完整總結,此前的歷史只能通過當前的狀態去影響過程未來的演變。具體地說,如果一個問題被劃分各個階段之後,階段I中的狀態只能由階段I-1中的狀態通過狀態轉移方程得來,與其它狀態沒有關係,特別是與未發生的狀態沒有關係。從圖論的角度去考慮,如果把這個問題中的狀態定義成圖中的頂點,兩個狀態之間的轉移定義為邊,轉移過程中的權值增量定義為邊的權值,則構成一個有向無環加權圖,因此,這個圖可以進行“拓撲排序”,至少可以按它們拓撲排序的順序去劃分階段。
我們在這篇講義中主要講解最基礎的線性DP記憶記憶化解法。
其實我們可以發現,如果一個搜尋解法新增上了記憶化,那麼他就解決了“最優子結構”和“重疊子問題”,就變成了一個遞迴版本的動態規劃了。
說明:
接下來的例題當中我們會講解這些問題的for迴圈解法和記憶化搜尋寫法。
雖然for迴圈寫法在我們這節課當中寫起來更方便且很好理解,但是希望同學們務必瞭解並掌握 記憶化搜尋 寫法,因為我們接下來的幾節課程會與記憶化搜尋有非常重要的關係。
例題1 最長上升子序列
題目大意:
給你一個長度為 \(n\) 的數列 \(a_1,a_2, \cdots , a_n\) ,請你求出它的最長上升子序列的長度。
最長上升子序列:在不交換順序的情況從序列 \(a\) 中選出一些元素(子序列不需要連續)使得前一個元素必然比後一個元素小。對應的最長的上升子序列就是最長上升子序列。
我們一般簡稱“最長上升子序列”為 LIS(Longest Increasing Subsequence)。
解題思路:
設狀態 \(f[i]\) 表示以 \(a_i\) 結尾(並且包含 \(a_i\))的最長上升子序列長度,則:
- \(f[i]\) 至少為 \(1\);
- \(f[i] = \max (f[j])\) + 1,其中 \(j\) 滿足 \(0 \le j \lt i\) 且 \(a[j] \lt a[i]\) 。
程式碼演示
首先我們定義陣列和一些必要的變數:
int n, a[1010], f[1010], ans;其中:
- \(n\) 表示陣列元素個數;
- \(a\) 陣列用於存值, \(a[i]\) 表示陣列第 \(i\) 個元素的值;
- \(f\) 陣列用於存狀態, \(f[i]\) 表示以 \(a[i]\) 結尾的LIS長度;
- \(ans\) 用於存放我們最終的答案。
然後我們處理輸入:
cin >> n;
for (int i = 1; i <= n; i ++)
cin >> a[i];然後,我們演示一下用for迴圈的方式實現求解 \(f[1]\) 到 \(f[n]\):
for (int i = 1; i <= n; i ++) {
f[i] = 1;
for (int j = 1; j < i; j ++) {
if (a[j] < a[i]) {
f[i] = max(f[i], f[j]+1);
}
}
}然後我們的答案就是 \(f[i]\) 的最大值:
for (int i = 1; i <= n; i ++)
ans = max(ans, f[i]);
cout << ans << endl;那麼,使用搜索+記憶化的方式怎麼實現呢?如下:
int dfs(int i) {
if (f[i]) return f[i];
f[i] = 1;
for (int j = 1; j < i; j ++)
if (a[j] < a[i])
f[i] = max(f[i], dfs(j)+1);
return f[i];
}記憶化搜尋 又被稱為 備忘錄 ,而我們這裡的備忘錄就是我們的 \(f[i]\) 。
- 如果
dfs(i)是第一次被呼叫,\(f[i]=0\),會執行一系列的計算; - 但是如果
dfs(i)不是第一次被呼叫,則必然 \(f[i] \gt 0\),所以dfs(i)會直接返回 \(f[i]\) 的值,這樣就避免了子問題的重讀計算。
所以我在函式的最開始就進行了判斷:
如果 \(f[i]\) 不為零,則直接返回 \(f[i]\)。
否則再進行計算。
然後,我們在可以通過如下方式計算答案:
for (int i = 1; i <= n; i ++)
ans = max(ans, dfs(i));
cout << ans << endl;一般形式的完整程式碼:
#include <bits/stdc++.h>
using namespace std;
int n, a[1010], f[1010], ans;
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++) {
f[i] = 1;
for (int j = 1; j < i; j ++) {
if (a[j] < a[i])
f[i] = max(f[i], f[j]+1);
}
}
for (int i = 1; i <= n; i ++)
ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}記憶化搜尋形式的完整程式碼:
#include <bits/stdc++.h>
using namespace std;
int n, a[1010], f[1010], ans;
int dfs(int i) {
if (f[i]) return f[i];
f[i] = 1;
for (int j = 1; j < i; j ++)
if (a[j] < a[i])
f[i] = max(f[i], dfs(j)+1);
return f[i];
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++)
ans = max(ans, dfs(i));
cout << ans << endl;
return 0;
}例題2 最大欄位和
題目大意:
我們可以把“欄位”理解為“連續子序列”。
最大欄位和問題就是求解所有連續子序列的和當中最大的那個和。
解題思路:
首先我們定義狀態 \(f[i]\) 表示以 \(a[i]\) 結尾(並且包含\(a[i]\))的最大欄位和。
那麼我們可以得到狀態轉移方程:
\(f[i] = \max(f[i-1], 0) + a[i]\)
首先我們初始化及輸入的部分如下(座標從\(1\)到\(n\)):
int n, a[1010], f[1010], ans;
cin >> n;
for (int i = 1; i <= n; i ++)
cin >> a[i];然後以一般方式求解的方式如下:
for (int i = 1; i <= n; i ++)
f[i] = max(f[i-1], 0) + a[i];然後我們的答案就是所有 \(f[i]\) 的最大值:
for (int i = 1; i <= n; i ++)
ans = max(ans, f[i]);
cout << ans << endl;遞迴形式,我們同樣開一個函式 dfs(i) 用於返回 \(f[i]\) 的值。
但是這裡我們無法通過 \(f[i]\) 的值確定 \(f[i]\) 是否已經求出來,所以我再開一個bool型別的 \(vis\) 陣列,通過 \(vis[i]\) 來判斷 \(f[i]\) 是否已經求過了。
bool vis[1010];記憶化搜尋實現如下:
int dfs(int i) {
if (i == 0) return 0; // 邊界條件
if (vis[i]) return f[i];
vis[i] = true;
return f[i] = max(dfs(i-1), 0) + a[i];
}注意:搜尋/遞迴一定要注意邊界條件。
然後,答案的求解方式1如下:
ans = dfs(1);
for (int i = 2; i <= n; i ++)
ans = max(ans, dfs(i));
cout << ans << endl;答案的另一種求解方式如下:
dfs(n);
ans = f[1];
for (int i = 2; i <= n; i ++)
ans = max(ans, f[i]);
cout << ans << endl;有沒有發現,在這裡我就呼叫了一次 \(dfs(n)\) ,所有的 \(f[i](1 \le i \le n)\) 的值就都求出來了呢。
因為我在第一次求 \(dfs(n)\) 的時候,會呼叫 \(dfs(n-1)\) ,而第一次 \(dfs(n-1)\) 會呼叫 \(dfs(n-2)\) ,……,第一次 \(dfs(2)\) 會呼叫 \(dfs(1)\)。
所以呼叫一下 \(dfs(n)\) ,我就把所有的 \(f[i]\) 都求出來了。
一般形式的完整實現程式碼如下:
#include <bits/stdc++.h>
using namespace std;
int n, a[1010], f[1010], ans;
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
for (int i = 1; i <= n; i ++)
f[i] = max(f[i-1], 0) + a[i];
for (int i = 1; i <= n; i ++)
ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}記憶化搜尋的完整實現程式碼如下:
#include <bits/stdc++.h>
using namespace std;
int n, a[1010], f[1010], ans;
bool vis[1010];
int dfs(int i) {
if (i == 0) return 0; // 邊界條件
if (vis[i]) return f[i];
vis[i] = true;
return f[i] = max(dfs(i-1), 0) + a[i];
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
// ans = dfs(1);
// for (int i = 2; i <= n; i ++)
// ans = max(ans, dfs(i));
dfs(n);
ans = f[1];
for (int i = 1; i <= n; i ++)
ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}例題3 數塔問題
題目大意:
有如下所示的數塔,要求從頂層走到底層,若每一步只能走到相鄰的結點,則經過的結點的數字之和最大是多少?
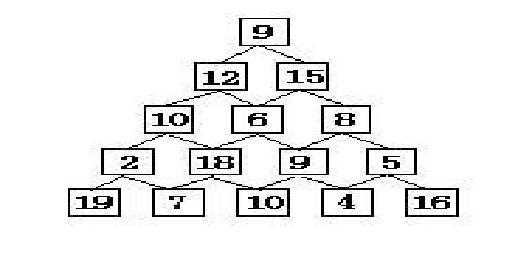
解題思路:
首先我們做一些假設:總共有 \(n\) 行,最上面的那行是第 \(1\) 行,最下面的那行是第 \(n\) 行,我們用 \((i,j)\) 來表示第 \(i\) 行第 \(j\) 個格子,用 \(a[i][j]\) 表示 \((i,j)\) 格子存放的值。
我們可以發現,從 \((i,j)\) 往下走走到最底層的最大數字和與從最下面的格子往上走走到 \((i,j)\) 的最大數字和是相等的。
所以我們可以把問題變成:求從最底下任意一個格子往上走走到 (1,1) 的最大數字和。
可以發現,經過這樣一下思維的轉換,我們就把一個“自頂向上”的問題轉換成了一個“自底向上”的問題。
(請好好體會 “自頂向下” 和 “自底向上” 這兩個概念,因為我們這道題接下來還會在另一個情景中討論這兩個概念)
我們可以發現,除了最底層(第 \(i\) 層)是直接走到的意外,上層的所有 \((i,j)\) 不是從 \((i+1,j)\) 走上來的,就是從 \((i+1, j+1)\) 走上來的。
所以我們不妨設 \(f[i][j]\) 表示從最底層任意一個位置往上走走到 \((i,j)\) 位置的最大數字和。
可以推匯出:
- 當 \(i=n\) 時,\(f[i][j] = a[i][j]\);
- 當 \(i \lt n\) 時, \(f[i][j] = \max(f[i+1][j], f[i+1][j+1]) + a[i][j]\)
在推導的過程中,記得從 \(n\) 到 \(1\) 遍歷 \(i\) ,因為高層的狀態要先通過低層的狀態推匯出來。
一般形式的主要實現程式碼段如下:
for (int i = n; i >= 1; i --) { // 自底向上
for (int j = 1; j <= n; j ++) {
if (i == n)
f[i][j] = a[i][j];
else
f[i][j] = max(f[i+1][j], f[i+1][j+1]) + a[i][j];
}
}可以發現,我們採用一般形式的寫法,是先求解較低層的轉態,然後通過低層的轉態推匯出高層的狀態,所以我們也說這種實現思想是 自底向上 的。
講完一般形式的實現方式,我們再來講解使用 記憶化搜尋 的形式進行求解的實現方式。
我們同樣還是要定義一個狀態 \(f[i][j]\) 表示從最底層任何一個位置走到 \((i,j)\) 的最大數字和(和上面的描述一樣)。
但是我們不是以上面的一般形式來求解 \(f[i][j]\) ,而是開一個函式 dfs(int i, int j) 來求解 \(f[i][j]\)。
那麼,我們怎麼樣來進行 記憶化 :即:判斷當前的 \(f[i][j]\) 已經訪問過呢?
因為一開始 \(f[i][j]\) 均為 \(0\),如果所有的數塔中的元素 \(a[i][j]\) 均 \(\gt 0\) ,那麼 \(f[i][j]\) 一旦求過則 \(f[i][j]\) 必然也 \(\gt 0\)。
但是如果 \(a[i][j] \ge 0\)(即 \(a[i][j]\) 可以為 \(0\))或者 \(a[i][j]\) 可以是負數的情況下,我們就不能靠 \(f[i][j]\) 是否為 \(0\) 來判斷 \((i,j)\) 這個格子有沒有訪問過了( 仔細思考一下為什麼 )。
所以最靠譜,最不容易錯的方式就是跟採用跟例2一樣的方式,開一個二維 \(vis\) 陣列, 用 \(vis[i][j]\) 來標識 \((i, j)\) 是否訪問過。
記憶化搜尋形式的主要程式碼片段如下:
int dfs(int i, int j) { // dfs(i,j)用於計算並返回f[i][j]的值
if (vis[i][j]) return f[i][j];
vis[i][j] = true;
if (i == n) // 邊界條件——最底層
return f[i][j] = a[i][j];
return f[i][j] = max(dfs(i+1, j), dfs(i+1, j+1)) + a[i][j];
}一般形式的完整程式碼如下:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 101;
int n, a[maxn][maxn], f[maxn][maxn];
int main() {
cin >> n;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= i; j ++)
cin >> a[i][j];
for (int i = n; i >= 1; i --) { // 自底向上
for (int j = 1; j <= n; j ++) {
if (i == n) f[i][j] = a[i][j];
else f[i][j] = max(f[i+1][j], f[i+1][j+1]) + a[i][j];
}
}
cout << f[1][1] << endl;
return 0;
}記憶化搜尋的完整程式碼如下:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 101;
int n, a[maxn][maxn], f[maxn][maxn];
bool vis[maxn][maxn];
int dfs(int i, int j) { // dfs(i,j)用於計算並返回f[i][j]的值
if (vis[i][j]) return f[i][j];
vis[i][j] = true;
if (i == n) // 邊界條件——最底層
return f[i][j] = a[i][j];
return f[i][j] = max(dfs(i+1, j), dfs(i+1, j+1)) + a[i][j];
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= i; j ++)
cin >> a[i][j];
cout << dfs(1, 1) << endl;
return 0;
}
