一曲新詞酒一杯，去年天氣舊亭臺。夕陽西下幾時回？
無可奈何花落去，似曾相識燕歸來。小園香徑獨徘徊。
———《浣溪沙·一曲新詞酒一杯》——晏殊

更多精彩內容請關注微信公眾號 “優化與演算法”

上一期介紹了低秩矩陣填充問題，這一期介紹一下低秩稀疏矩陣恢復問題。

1. 低秩矩陣恢復

將一個矩陣 \(\bf{D}~(\bf {D} = \bf {A_0} +\bf E_0)\) 分解為一個低秩矩陣部分 \(\bf{A}\) 和一個獨立同分布的高斯矩陣 \(\bf{E}\) 的問題是經典的主成分分析（PCA）問題，可以通過對矩陣 \(\bf{D}\) 進行奇異值分解得到最優解。

然而，當矩陣 \(\bf{E_0}\) 為稀疏的噪聲矩陣時，PCA不再適用於解決這個問題。此時 ，將一個矩陣 \(\bf{D}~(\bf {D} = \bf {A_0} +\bf E)\) 分解為一個低秩矩陣部分 \(\bf{A}\) 和一個稀疏矩陣部分 \(\bf{E}\) 的問題可以建模為下述優化問題：

\[\begin{array}{l} \mathop {\min }\limits_{{\bf{A}},{\bf{E}}} ~~~rank({\bf{A}}) + \lambda {\left\| {\bf{E}} \right\|_0} \\ s.t.~~~{\bf{D}} = {\bf{A}} + {\bf{E}} \\ \end{array}~~~~~(1)\]

其中 \({\bf{D}},{\bf{A}},{\bf{E}},{{\bf{A}}_0},{{\bf{E}}_0}{ \in \mathbb{R}^{m \times n}}\)，\(\bf D\) 是觀測矩陣。(1)式中 \(rank(\bf A)\) 和 \({\left\| {\bf{E}} \right\|_0}\) 都是非線性且非凸的，優化起來非常困難，這個問題也被稱為主成分追蹤（Principal component pursuit, PCP）。幸運的是我們提前知道一些先驗資訊，即矩陣 \(\bf A\) 是低秩的且矩陣 \(\bf E\) 是稀疏的，從上一期介紹的關於矩陣填充理論中可知，矩陣的秩和 \(\ell_0\) 範數問題都可以進行凸鬆弛，從而為求解上述問題提供了途徑。由於矩陣的核範數是矩陣秩的凸包絡，矩陣的（1,1）範數是矩陣0範數的凸包絡，因此可以將問題(1)鬆弛為如下凸優化問題：
\[\begin{array}{l} \mathop {\min }\limits_{{\bf{A}},{\bf{E}}}~~~ {\left\| {\bf{A}} \right\|_*} + \lambda {\left\| {\bf{E}} \right\|_{1,1}} \\ s.t.~~~{\bf{D}} = {\bf{A}} + {\bf{E}} \\ \end{array}~~~~~~(2)\]

求解式(2)也稱為魯棒主成分分析(RPCA)。

文獻[1]中指出，只要低秩矩陣 \(\bf{A_0}\) 的奇異值分佈合理且稀疏矩陣的非零元素均勻分佈，那麼凸優化問題PCP就能夠以接近1的概率從未知的任意誤差中恢復出原始低秩矩陣 \(\bf A_0\) 來。

求解(2)式的演算法可以分為如下幾大類：

1. 迭代閾值演算法
   對於PCP問題時，迭代閾值演算法(Iterative Thresholding, IT) 通過交替更新矩陣 \(\bf A\) 和 \(\bf E\) 來求解。IT演算法的迭代形式簡單且收斂，但它的收斂速度比較慢，且難以選取合適的步長。因此，IT演算法具有有限的應用範圍。
2. 加速近端梯度演算法
   加速近端梯度演算法(Accelerated Proximal Gradient, APG)的主要思想是利用了Nesterov加速，使演算法能夠快速收斂。
3. 對偶方法
   將原問題轉化為其對偶問題(非線性、非光滑)，並使用最速上升法等可以求解。對偶方法比APG演算法具有更好的可擴充套件性，這是因為在每次迭代過程中對偶方法不需要矩陣的完全奇異值分解。
4. 增廣拉格朗日乘子法

這些方法都非常經典，這裡不再細述，總的來說，只要將問題轉化為凸問題，就有一大堆方法可以用來求解。這裡僅介紹一種增廣拉格朗日乘子演算法，即交替方向方法(Alternating direction methods, ADM)，也稱為不精確拉格朗日乘子法(Inexact ALM, IALM)。
下面給出上述幾種演算法的比較(資料來源於網路)

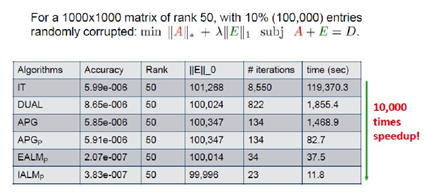
2. 交替方向演算法(ADM)

對於優化問題(2)，首先構造增廣拉格朗日函式：
\[L({\bf{A}},{\bf{E}},{\bf{Y}},u) = {\left\| {\bf{A}} \right\|_*} + \lambda {\left\| {\bf{E}} \right\|_{1,1}} + \left\langle {{\bf{Y}},{\bf{D}} - {\bf{A}} - {\bf{E}}} \right\rangle + \frac{u}{2}\left\| {{\bf{D}} - {\bf{A}} - {\bf{E}}} \right\|_F^2~~~(3)\]

當 \({\bf{Y}} = {{\bf{Y}}_k},u = {u_k}\) 時，使用交替方法求解塊優化問題：
\[\mathop {\min }\limits_{{\bf{A}},{\bf{E}}} L({\bf{A}},{\bf{E}},{{\bf{Y}}_k},{u_k})~~~(4)\]

使用精確拉格朗日乘子法(Exact ALM, EALM)交替迭代矩陣 \(\bf A\) 和 \(\bf E\)，直到滿足終止條件為止。若 \({\bf{E}} = {\bf{E}}_{k + 1}^j\)，則
\[\begin{array}{l} {\bf{A}}_{k + 1}^{j + 1} = \arg \mathop {\min }\limits_{\bf{A}} L({\bf{A}},{\bf{E}}_{k + 1}^j,{{\bf{Y}}_k},{u_k}) \\ = \arg \mathop {\min }\limits_{\bf{A}} {\left\| {\bf{A}} \right\|_*} + \frac{{{u_k}}}{2}\left\| {{\bf{A}} - ({\bf{D}} - {\bf{E}}_{k + 1}^j + \frac{{{{\bf{Y}}_k}}}{{{u_k}}})} \right\|_F^2 \\ = {D_{\frac{1}{{{u_k}}}}}({\bf D} - {\bf{E}}_{k + 1}^j + \frac{{{{\bf{Y}}_k}}}{{{u_k}}}) \\ \end{array}~~~(5)\]

再根據 \({\bf{A}}_{k + 1}^{j + 1}\) 更新矩陣 \(\bf E\)：
\[\begin{array}{l} {\bf{E}}_{k + 1}^{j + 1} = \arg \mathop {\min }\limits_{\bf{E}} L({\bf{A}}_{k + 1}^{j + 1},{\bf{E}},{{\bf{Y}}_k},{u_k}) \\ = \arg \mathop {\min }\limits_{\bf{E}} \lambda {\left\| {\bf{E}} \right\|_{1,1}} + \frac{{{u_k}}}{2}\left\| {{\bf{E}} - ({\bf{D}} - {\bf{A}}_{k + 1}^{j + 1} + \frac{{{{\bf{Y}}_k}}}{{{u_k}}})} \right\|_F^2 \\ = {S_{\frac{\lambda }{{{u_k}}}}}({\bf D} - {\bf{A}}_{k + 1}^{j + 1} + \frac{{{{\bf{Y}}_k}}}{{{u_k}}}) \\ \end{array}~~~(6)\]

記 \({\bf{A}}_{k + 1}^{\rm{*}}\) 和 \({\bf{E}}_{k + 1}^{\rm{*}}\) 分別為 \({\bf{A}}_{k + 1}^{j + 1}\) 和 \({\bf{E}}_{k + 1}^{j + 1}\) 的精確值，則矩陣 \(\bf Y\) 的更新公式為：
\[{{\bf{Y}}_{k{\rm{ + }}1}}{\rm{ = }}{{\bf{Y}}_k}{\rm{ + }}{u_k}({\bf{D}} - {\bf{A}}_{k + 1}^{\rm{*}} - {\bf{E}}_{k + 1}^{\rm{*}})~~~(7)\]

引數 \({u_k}\) 可以更新如下：
\[{u_{k + 1}} = \left\{ {\begin{array}{*{20}{c}} {\rho {u_k}~~~\frac{{{u_k}{{\left\| {{\bf{E}}_{k + 1}^{\rm{*}}{\rm{ - }}{\bf{E}}_k^{\rm{*}}} \right\|}_F}}}{{{{\left\| {\bf{D}} \right\|}_F}}} < \varepsilon } \\ {{u_k}~~~~~~~~otherwise} \\ \end{array}} \right.~~~~(8)\]

其中 \(\rho>1\) 為常數，\(\varepsilon>0\) 為一個小的正數。

上述精確ALM方法在內迴圈中要多次更新，進行多次奇異值分解，為此文獻[1]提出了非精確拉格朗日乘子法(Inecact ALM, IALM)，它不需要在每次外迴圈開始之前要求 \(\mathop {\min }\limits_{{\bf{A}},{\bf{E}}} L({\bf{A}},{\bf{E}},{{\bf{Y}}_k},{u_k})\) 的精確解，也就是去掉了ALM方法的內迴圈，其更新公式變成了如下形式：
\[\begin{array}{l} {{\bf{A}}_{k + 1}} = \arg \mathop {\min }\limits_{\bf{A}} L({\bf{A}},{{\bf{E}}_{k + 1}},{{\bf{Y}}_k},{u_k}) \\ ~~~~~~~~~= {D_{\frac{1}{{{u_k}}}}}({\bf{D}} - {{\bf{E}}_{k + 1}} + \frac{{{{\bf{Y}}_k}}}{{{u_k}}}) \\ \end{array}~~~(9)\]

\[\begin{array}{l} {{\bf{E}}_{k + 1}} = \arg \mathop {\min }\limits_{\bf{E}} L({{\bf{A}}_{k + 1}},{\bf{E}},{{\bf{Y}}_k},{u_k}) \\ {~~~~~~~~~=S_{\frac{\lambda }{{{u_k}}}}}({\bf{D}} - {{\bf{A}}_{k + 1}} + \frac{{{{\bf{Y}}_k}}}{{{u_k}}}) \\ \end{array}~~~~(10)\]

上面式子中的奇異值閾值運算元 \({D_{\frac{1}{{{u_k}}}}}( \cdot )\) 和軟閾值運算元 \({S_{\frac{\lambda }{{{u_k}}}}}( \cdot )\) 的定義參見上一期<低秩矩陣填充|奇異值閾值演算法>。

4. 低秩矩陣恢復的應用

低秩矩陣恢復技術是一個非常有研究價值和實用價值的技術，它的應用也非常廣泛，比如說：

1. 視訊背景建模。
   

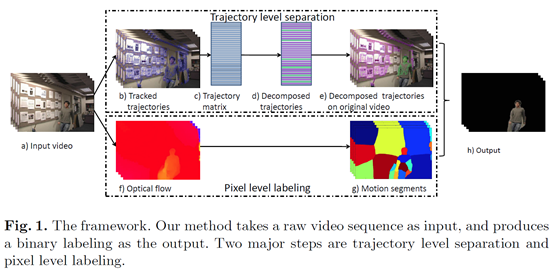
2. 影象恢復(去光照、陰影等)
   

3. 影象類別標籤淨化
4. 文字主題分析
5. 音樂詞曲分離

6. 影象矯正與去噪
   

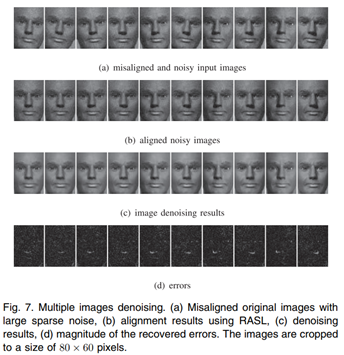
7. 影象對齊

5. 模擬

ADM演算法matlab程式碼如下：

function [L,S] = pcp_ad(M,u,lambda,itemax,tol)
% solve PCP problem by ADM algorithm
% v1.0 2020-1-1
% function：solve the following optimization problem
%                  min  ||X||*+lambda||E||_F
%                  s.t. M = A+E

% initialize S0 and Y0 and L0
[m,n] = size(M) ;
S = zeros(m,n) ;
Y = S ;
L = S ;

% the observed matrix can contain non number
unobserved = isnan(M);
M(unobserved) = 0;

if nargin < 2
    lambda = 1 / sqrt(max(m,n));
end
if nargin < 3
    u = 10*lambda;
end
if nargin < 4
    tol = 1e-6;
end
if nargin < 5
    itemax = 1000;
end

for ii = 1:itemax
    L = sig_thre(M-S+(1/u)*Y,(1/u)) ;
    S = soft_thre(M-L+(1/u)*Y, lambda/u) ;
    Z = M-L-S ;
    Y = Y+u*Z ;
    error = norm(M-L-S,'fro')/norm(M,'fro') ;
    if (ii == 1) || (mod(ii, 10) == 0) || (error < tol)
        fprintf(1, 'iter: %04d\terr: %f\trank(L): %d\tcard(S): %d\n', ...
            ii, error, rank(L), nnz(S));
    end
    if error<tol
        break;
    end
end

數值測試程式碼：

% solve PCP problem by alternating direction method
clear
clc

m = 100 ;
n = 100 ;
r = 0.05*n ;
rate = 0.05 ;
% Generating a low rank matrix
LL = randn(m,r)/sqrt(m)*randn(r,n)/sqrt(n) ;
% Generating a large sparse noise matrix (Bernoulli matrix)
SS = randi([0,1],m,n) ;
SS(SS==0) = -1 ;

% sampling
ss = SS(:) ;
index = sort(randperm(m*n,ceil(rate*n*m))) ;
ss1 = zeros(m*n,1) ;
ss1(index) = ss(index) ;
SS = reshape(ss1,m,n) ;
M = LL+SS ;

lambda = 1/sqrt(max(m,n)) ;
u = 10*lambda ;

% [L,S] = pcp_ad(M,u,lambda,1000) ;
[L,S] = RobustPCA(M,lambda,u);
% [L,S] = pcp_ad(M,u,lambda,500,1e-8);
% [L,S] = adm_lrr(M);
MM = M-L-S ;

norm(M-MM,'fro')/norm(M,'fro')
norm(M-L-S,'fro')/norm(M,'fro')
norm(L-LL,'fro')/norm(LL,'fro')
norm(S-SS,'fro')/norm(SS,'fro')

執行上面程式，顯示結果norm(M-L-S,'fro')/norm(M,'fro')約為9e-7，norm(L-LL,'fro')/norm(LL,'fro')約為1e-5。

低秩影象恢復模擬程式：

% low rank and sparse noise image recovery
clear
clc

A = imread('C:\xxx\xxx\xxx.bmp') ;

WW = double(A) ;
a1 = double(A(:,:,1)) ;
a2 = double(A(:,:,2)) ;
a3 = double(A(:,:,3)) ;
[M,N] = size(a1);
X = zeros(M,N,3);
    
for jj = 1:3
    lambda = 1*1 / sqrt(max(M,N)); 
    u =  1*lambda;
    [ X(:,:,jj),S(:,:,jj)] = RobustPCA(WW(:,:,jj),lambda,u,1e-8,200) ;
end

figure(1)
subplot(3,1,1)
imshow(A)
title("原圖",'fontsize',12)
subplot(3,1,2)
imshow(uint8(X))
title("低秩圖",'fontsize',12)
d = S ;
d(d<20) = 255 ;
subplot(3,1,3)
imshow(uint8(d))
title("噪聲圖",'fontsize',12)

低秩影象恢復結果如下：

從上面影象恢復結果來看，效果還不錯。

參考文獻

[1] Candès, E. J., Li, X., Ma, Y., & Wright, J. (2011). Robust principal component analysis?. Journal of the ACM (JACM), 58(3), 11.
[2] 史加榮, 鄭秀雲, 魏宗田, & 楊威. (2013). 低秩矩陣恢復演算法綜述. 計算機應用研究, 30(6), 1601-1605.
[3] Cui, X., Huang, J., Zhang, S., & Metaxas, D. N. (2012, October). Background subtraction using low rank and group sparsity constraints. In European Conference on Computer Vision (pp. 612-625). Springer, Berlin, Heidelberg.
[4] Wright, J., Ganesh, A., Rao, S., Peng, Y., & Ma, Y. (2009). Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Advances in neural information processing systems (pp. 2080-2088).
[5] Peng, Y., Ganesh, A., Wright, J., Xu, W., & Ma, Y. (2012). RASL: Robust alignment by sparse and low-rank decomposition for linearly correlated images. IEEE transactions on pattern analysis and machine intelligence, 34(11), 2233-2246.

更多精彩內容請關注訂閱號優化與演算法

更多精彩內容請關注微信公眾號 “優化與演算法