你沒聽過的梅森旋轉演算法
(標準開頭)
如果單獨提梅森旋轉演算法可能大家都很陌生,但如果說到C++11的random可能大家就都熟悉多了。事實上,C++,python等多種計算機語言的隨機數都是通過梅森旋轉演算法產生的。(也有一個稱呼是梅森纏繞演算法)
那,本文就著重介紹這個梅森螺旋旋轉演算法
(演算法本身挺學術的,我努力寫得輕鬆點)
先在這裡感謝一下@dgklr大佬的引導。如果沒有他提及,筆者可能還不知道這個演算法。
旋轉演算法簡介
梅森旋轉演算法,也可以寫作MT19937。是有由松本真和西村拓士在1997年開發的一種能快速產生優質隨機數的演算法。
其實這個演算法跟梅森沒有什麼關係,它之所以叫做是梅森旋轉演算法是因為它的迴圈節是2^19937-1,這個叫做梅森素數。
如果看過我的那篇隨機數的文章應該知道關於偽隨機的一些知識。這個隨機演算法之所以說是產生“優質“”隨機數,特點就是它的迴圈節特別長。而且產生的數分佈是比較平均的。
可能有的同學對這個迴圈節有點質疑。可能覺得2^19937-1有點短?
我在這裡大概給一個概念:
銀河系中的恆星數量級10^11
撒哈拉沙漠中的沙子數數量級是10^26
宇宙中目前可觀察的粒子數量級是10^87
2^19937數量級是10^6001
這個比較大概心裡有數了吧
相差的已經不止是一個數量級了
同時他在623維中的分佈都十分的均勻(這個不用理解)
知道分佈平均就好了

(梅森鎮樓)
->continue
前置知識
分析這個演算法的原理需要的前置知識在網上講的都比較繞,我在這裡就通俗的科普一下,主要是認識這幾個名詞。
(用詞不準確輕噴)
線性反饋移位暫存器(LFSR)
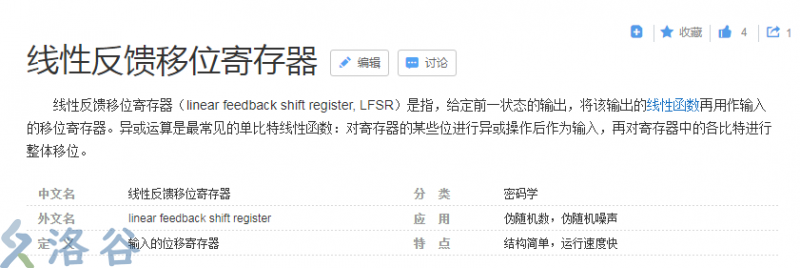
這個,就當它是隨機數發生器就完事了,不要太去糾結定義。後面會講。
本原多項式
簡單的說來就是沒法化簡的多項式
比如 y=x^4+x^2 就可以化簡
也是知道就好
級
計算機的一個二進位制單位(0或1)就是一級
這個應該比較好理解
反饋函式
這個應該是網上看別的部落格最繞的知識點
簡單地理解成告訴你你要對這個暫存器幹什麼的一個函式就好了
(看到這裡應該還沒懵吧)
異或
這個...
還要我科普嗎?
就是兩個數,如果都是0或都是1就輸出0,一個1一個0輸出1.
->continue
原理分析
這個旋轉演算法實際上是對一個19937級的二進位制序列作變換。
首先我們達成一個共識:
一個長度為n的二進位制序列,它的排列長度最長為2^n。
當然這個也是理論上的,實際上可能因為某些操作不當,沒挺到2^n個就開始迴圈了。
那麼如何將這個序列的排列撐滿2^n個,就是這個旋轉演算法的精髓。
如果反饋函式的本身+1是一個本原多項式,那麼它的迴圈節達到最長,即2^n-1
這個數學證明本文不作過多論述,有興趣者可以自己查閱資料
個人感覺單講知識點挺難懂的(筆者就是這麼被坑的)
我們就拿一個4級的暫存器模擬一下:
我們這裡使用的反饋函式是 y=x^4+x^2+x+1(這個不是本原多項式,只是拿來好理解) 這個式子中x^4,x^2,x的意思就是我們每次對這個二進位制序列的從後往前數第4位和第2位做異或運算 ,然後再拿結果和最後一位做異或運算。把最後的結果放到序列的開頭,整個序列後移一位,最後一位捨棄(或者輸出)
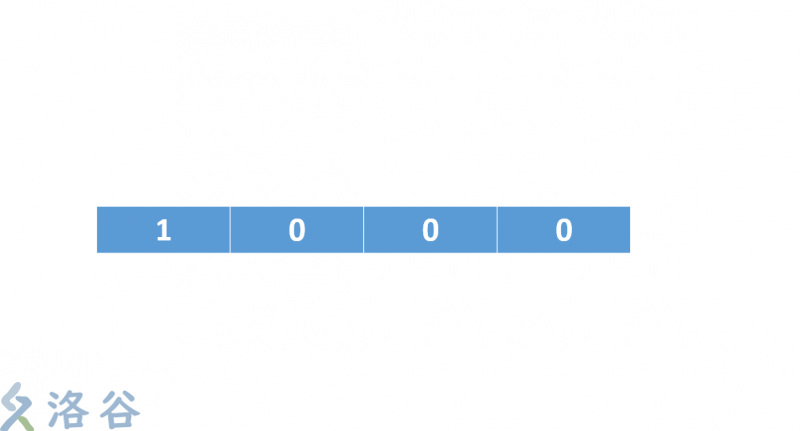
- 初始陣列 { 1 , 0 , 0 , 0 } (為什麼不是 0,0,0,0 你們可以自己想想,文章末尾揭曉)
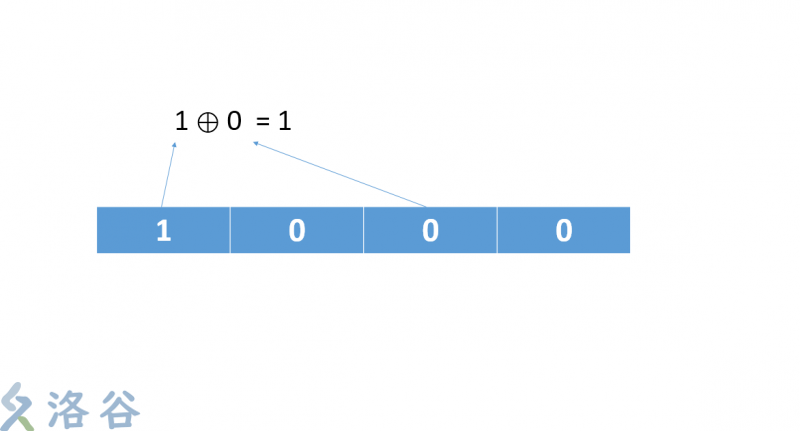
- 將它的第四位和第二位抓出來做異或運算
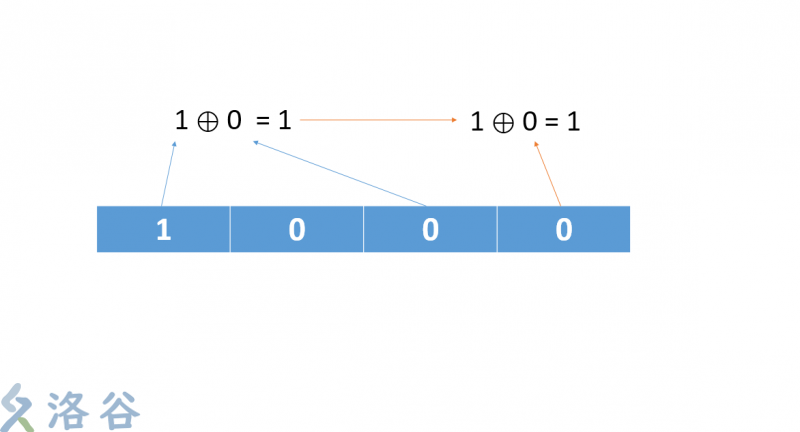
- 把剛剛的運算結果和最後一位再做一次運算
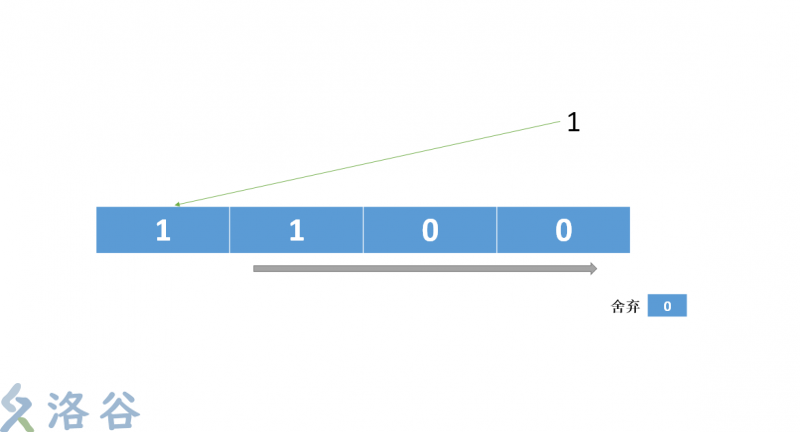
- 把最後的運算結果放到第一位,序列後移。最後一位被無情的拋棄
這就是一次運算,然後這個演算法就是不斷迴圈這幾步,從而不斷偽隨機改變這個序列。

上圖是一個網上找的一個4級暫存器的模擬過程
大家可以推一下,它所使用的反饋函式(y=x^4+x+1)
因為這個是本原多項式
所以他最後的迴圈節是2^4-1=15
運算結果如下:

(圖片摘自原文連結)
關於旋轉
可能有人到這裡還沒看出“旋轉”在哪裡。因為我們每次計算出來的結果會放在開頭,序列後移一位。看起來就像陣列在向後旋轉...
(本來想做gif的,後來不知道怎麼做出旋轉)
大家自行腦補

->continue
程式碼實現
(筆者很懶,直接搬原始碼出處的程式碼)
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <time.h>
using namespace std;
bool isInit;
int index;
int MT[624]; //624 * 32 - 31 = 19937
void srand(int seed)
{
index = 0;
isInit = 1;
MT[0] = seed;
for(int i=1; i<624; i++)
{
int t = 1812433253 * (MT[i-1] ^ (MT[i-1] >> 30)) + i;
MT[i] = t & 0xffffffff; //取最後的32位
}
}
void generate()
{
for(int i=0; i<624; i++)
{
// 2^31 = 0x80000000
// 2^31-1 = 0x7fffffff
int y = (MT[i] & 0x80000000) + (MT[(i+1) % 624] & 0x7fffffff);
MT[i] = MT[(i + 397) % 624] ^ (y >> 1);
if (y & 1)
MT[i] ^= 2567483615;
}
}
int rand()
{
if(!isInit)
srand((int)time(NULL));
if(index == 0)
generate();
int y = MT[index];
y = y ^ (y >> 11);
y = y ^ ((y << 7) & 2636928640);
y = y ^ ((y << 15) & 4022730752);
y = y ^ (y >> 18);
index = (index + 1) % 624;
return y; //筆者注:y即為產生的隨機數
}
int main()
{
srand(0); //設定隨機種子
int cnt = 0;
for(int i=0; i<1000000; i++) //下面的迴圈是用來判斷隨機數的奇偶概率的
{
if(rand() & 1)
cnt++;
}
cout<<cnt / 10000.0<<"%"<<endl;
return 0;
}->continue
填一下前面的坑
這裡回答一下前面的那個問題:
為什麼迴圈節是2^n-1而不是2^n
這個問題的答案和為什麼初始序列不能是 { 0 , 0 , 0 , 0 }是一樣的,因為如果全是0的話,無論怎麼異或運算都不能產生迴圈。那麼還怎麼偽隨機啊。
因為不能是全0,所以迴圈節要-1
(* o *)
( ⊕ o ⊕ )
最後非常感謝你能有耐心讀到這裡。
大家都很強,可與之共勉
