一、初探二分查詢

在面試的時候，尤其的一面，感覺讓你手寫二分，還真的不一定就能很快寫出來，所以在此總結分享給大家

1 二分查詢是什麼？

”查詢“顧名思義是在一堆數去找出我們需要的數，但是我們又想更快的找出我們需要找的數，所以我們就儘量的減少查詢比較的次數。"二分"就是分成兩份來減少我們查詢次數。

不急不急，假設我們這裡有十個數，我們來畫圖看看這是個什麼神操作。

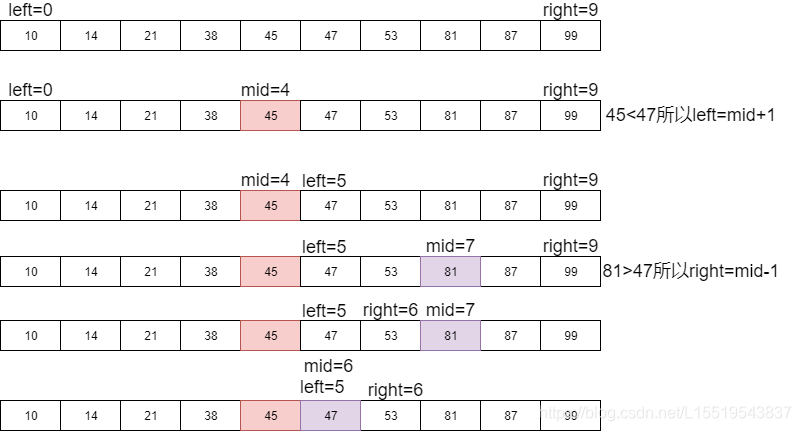
從上圖我們知道，我們每次都和區間的中間項值進行比較，從而縮小查詢區間的值。

2 時間複雜度？

這裡我們假設搜尋區間一共n個數，第一次切分n/2,第二次n/4,第三次n/8..........n/2(k).這是一個等比數列，n/2(k)=1,k=log2n,那麼時間複雜度為logn.

二 、二分的注意事項

1 二分查詢要求資料必須是有序的。
2 二分查詢依賴於陣列隨機查詢的特性，要求記憶體連續

三 、二分的實現

1 第一種小白寫法

int BinarySerach(vector<int>& nums, int target) {
    int left = 0, right = nums.size();
    while (left < right) {
        int mid = (left+right)/2;
        if (nums[mid] == target) return mid;
        else if (nums[mid] < target) left = mid + 1;
        else right = mid;
    }
    return -1;
}
 

面試官發話了

2 方法二優化版
如果right和left比較的時候，兩者之和可能溢位。那麼改進的方法是mid=left+(right-left)/2.還可以繼續優化，我們將除以2這種操作轉換為位運算mid=left+((right-left)>>1).

哪有這麼簡單的事兒，大多數的筆試面試中可能會出現下面的幾種情況。

四 、二分的各種變種

這裡主要是看看原始陣列有重複數的情況。

1 查詢第一個值等於給定值的情況(查詢元素7)
思路

首先7與中間值a[4]比較，發現小於7，於是在5到9中繼續查詢，中間a[7]=7,但是這個數7不是第一次出現的。那麼我們檢查這個值的前面是不是等於7，如果等於7，說明目前這個值不是第一次出現的7，此時更新rihgt=mid-1.ok我們看看程式碼

int BinarySerach(vector<int>& nums, int n,int target) {
    int left = 0, right = n-1;
    while (left <= right) {
        int mid = left+((right-left)>>1);
        if (nums[mid]>value)
        {
            right=mid-1;
        } else if(nums[mid]<value)
        {
            left=mid+1;
        }else
        {
            if((mid==0)||(nums[mid-1]!=value))
            {
                return mid;
            }else
            {
                left=mid-1;
            }
        }
    return -1;
}

2 查詢最後一個值等於給定值的情況

假設nums[mid]這個值已經是最後一個元素了，那麼它肯定是要找到最後一個值。如果nums[mid]的下一個不等於value，那說明nums[mid]就是我們需要找到最後一個等於給定值的值。

int BinarySerach(vector<int>& nums, int n,int target) {
    int left = 0, right = n-1;
    while (left <= right) {
        int mid = left+((right-left)>>1);
        if (nums[mid]>value)
        {
            right=mid-1;
        } else if(nums[mid]<value)
        {
            left=mid+1;
        }else
        {
            if((mid==n-1)||(nums[mid+1]!=value))
            {
                return mid;
            }else
            {
                left=mid+1;
            }
        }
    return -1;
}

3 查詢第一個大於等於給定值的情況

1 如果nums[mid]小於要查詢的值，那麼我們需要查詢在[mid+1,right]之間，所以此時更新為left=mid+1
2 如果nums[mid]大於給定值value,這個時候需要檢視nums[mid]是不是我們需要找的第一個值大於等於給定值元素，如果nums[mid]前面沒有元素或者前面一個元素小於查詢的值，那麼nums[mid]就是我們需要查詢的值。相反
3 如果nums[mid-1]也是大於等於查詢的值，那麼說明查詢的元素在[left,mid-1]之間，所以我們需要將right更新為mid-1

int BinarySerach(vector<int>& nums, int n,int target) {
    int left = 0, right = n-1;
    while (left <= right) {
        int mid = left+((right-left)>>1);
        if (nums[mid]>=value)
        {
            if(mid==0||nums[mid-1]<value)
            {
                return mid;
            }else
            {
                right=mid-1;
            }
        }else
        {
            left=mid+1;
        }
    return -1;
}

4 查詢最後一個小於等於給定值的情況

1 如果nums[mid]小於查詢的值，那麼需要查詢的值肯定在[mid+1,right]之間，所以我們需要更新left=mid+1
2 如果nums[mid]大於等於給定的value，檢查nums[mid]是不是我們的第一個值大於等於給定值的元素

int BinarySerach(vector<int>& nums, int n,int target) {
    int left = 0, right = n-1;
    while (left <= right) {
        int mid = left+((right-left)>>1);
        if (nums[mid]>value)
        {
            right=mid-1;
        }else
        {
            if(mid==n-1||(nums[mid+1]>value))
            {
                return mid;
            }else
            {
                left=mid+1;
            }
        }
    return -1;
}

六 結尾

好了，今天文章就到這了，如果你讀到這裡了，老鐵麼麼噠！非常感謝！
點關注，不跑路

文章會首於與微信，可以微信搜尋[我是程式設計師小賤]第一時間檢視。

後面每週都會更新幾篇面試高頻題目和自己總結的文章，如果覺得學到了一點東西，來個三連擊，點贊，關注，分享。

創作不易，各位的支援和認可，就是我創作的最大動力，我們下篇文章見！

如果本篇部落格有任何錯誤，請批評指教，不勝感激 ！

相關推薦