演算法入門基礎
阿新 • • 發佈:2020-02-06
排序分類:
內部排序:把資料載入到記憶體中進行排序,適用於資料量小的情況。
外部排序:藉助外部的檔案等,資料量大,無法載入到記憶體。
常見分類如圖:
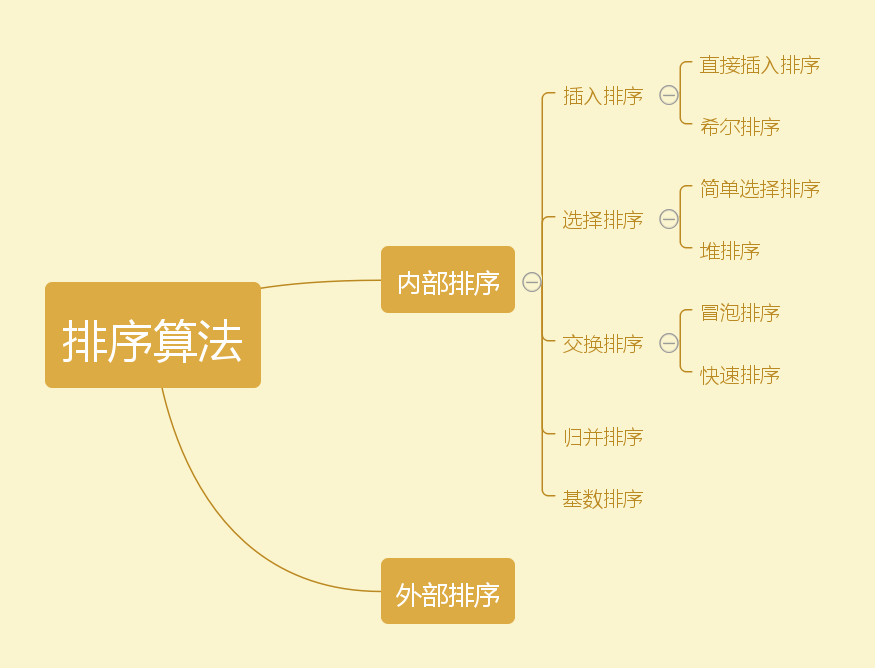
演算法複雜度
演算法複雜度分為時間複雜度和空間複雜度。其作用: 時間複雜度時間複雜度是指執行演算法所需要的計算工作量;而空間複雜度是指執行這個演算法所需要的記憶體空間。演算法的複雜性體執行該演算法時的計算機所需資源的多少上,計算機資源最重要的是時間和空間,即暫存器資源,因此複雜度分為時間和空間複雜度。
空間複雜度:
描述一個演算法所需要的空間大小,即佔用的內部記憶體,或者外部的記憶體大小,目前的裝置效能各方面發展較快,空間複雜度已經不是影響程式效能的主要因素。
時間複雜度:
概述:
時間複雜度是一個函式,它定性描述該演算法的執行時間。這是一個代表演算法輸入值的字串的長度的函式。時間複雜度常用大O符號表述,不包括這個函式的低階項和首項係數。使用這種方式時,時間複雜度可被稱為是漸近的,亦即考察輸入值大小趨近無窮時的情況。
時間頻度
一個語句執行次數稱為語句頻度或時間頻度,記為T(n)。演算法花費的時間與演算法中語句的執行次數成正比例,哪個演算法中語句執行次數多,它花費時間就多。
時間複雜度:
一般情況下,演算法中基本操作重複執行的次數是問題規模n的某個函式,用T(n)表示,若有某個輔助函式f(n),使得當n趨近於無窮大時,T(n)/f (n)的極限值為不等於零的常數,則稱f(n)是T(n)的同數量級函式。記作T(n)=O(f(n)),稱O(f(n)) 為演算法的漸進時間複雜度,簡稱時間複雜度
舉個栗子:int sum = 0; int b = 100; for(int i = 0; i<= b;i++){ sum += i; } // T(n) = n+1 = 100+1 sum = (1+b)*b/2 //同樣也可以計算出結果,但是T(n) = 1簡而言之,在
T(n)=O(f(n))中,當n趨近無窮大時,有T(n)/f(n) = c,極限值c是一個不為0 的常數,就叫 f(n) 是T(n)的同量級函式,若求得 f(n) = n ,則O(f(n)) =O(n).各時間複雜度增長曲線:

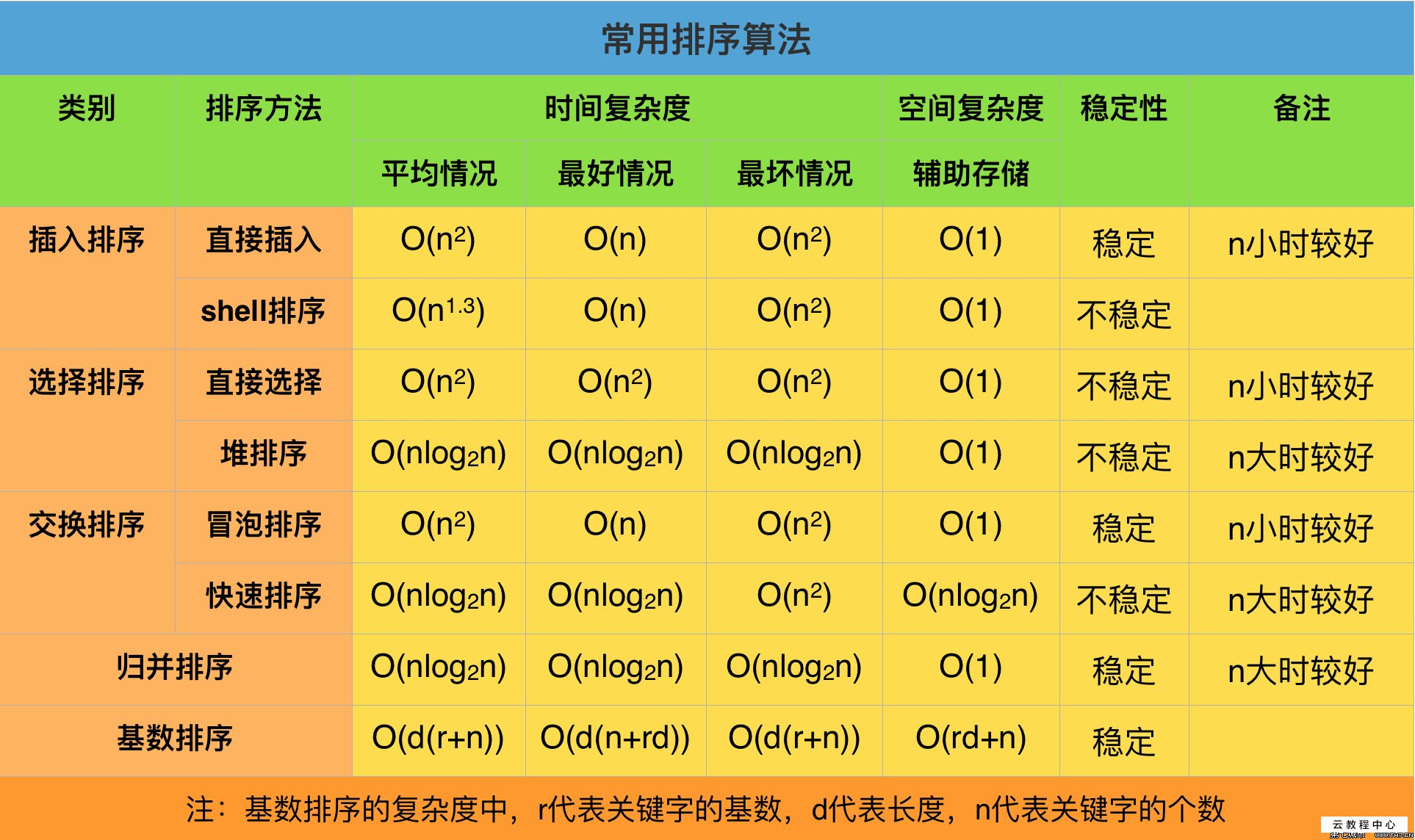
各演算法時間複雜度: