斐波拉契數列

首先我們來看看斐波拉契數列，這是一個大家都很熟悉的數列：

// f = [1, 1, 2, 3, 5, 8]
f(1) = 1;
f(2) = 1;
f(n) = f(n-1) + f(n -2); // n > 2

有了上面的公式，我們很容易寫出計算f(n)的遞迴程式碼：

function fibonacci_recursion(n) {
  if(n === 1 || n === 2) {
    return 1;
  }
  
  return fibonacci_recursion(n - 1) + fibonacci_recursion(n - 2);
}

const res = fibonacci_recursion(5);
console.log(res);   // 5
 

現在我們考慮一下上面的計算過程，計算f(5)的時候需要f(4)與f(3)的值，計算f(4)的時候需要f(3)與f(2)的值，這裡f(3)就重複算了兩遍。在我們已知f(1)和f(2)的情況下，我們其實只需要計算f(3)，f(4)，f(5)三次計算就行了，但是從下圖可知，我們總共計算了8次，裡面f(3), f(2), f(1)都有多次重複計算。如果n不是5，而是一個更大的數，計算次數更是指數倍增長。不考慮已知1和2的情況的話，這個遞迴演算法的時間複雜度是\(O(2^n)\)。

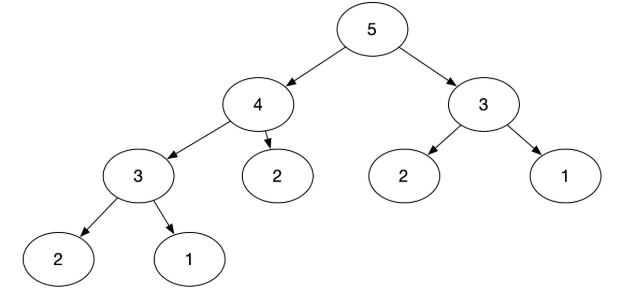
非遞迴的斐波拉契數列

為了解決上面指數級的時間複雜度，我們不能用遞迴演算法了，而要用一個普通的迴圈演算法。應該怎麼做呢？我們只需要加一個數組，裡面記錄每一項的值就行了，為了讓陣列與f(n)的下標相對應，我們給陣列開頭位置填充一個0

const res = [0, 1, 1];
f(n) = res[n];

我們需要做的就是給res陣列填充值，然後返回第n項的值就行了:

function fibonacci_no_recursion(n) {
  const res = [0, 1, 1];
  for(let i = 3; i <= n; i++){
    res[i] = res[i-1] + res[i-2];
  }
  
  return res[n];
}

const num = fibonacci_no_recursion(5);
console.log(num);   // 5

上面的方法就沒有重複計算的問題，因為我們把每次的結果都存到一個數組裡面了，計算f(n)的時候只需要將f(n-1)和f(n-2)拿出來用就行了，因為是從小往大算，所以f(n-1)和f(n-2)的值之前就算好了。這個演算法的時間複雜度是O(n)，比\(O(2^n)\)好的多得多。這個演算法其實就用到了動態規劃的思想。

動態規劃

動態規劃主要有如下兩個特點

1. 最優子結構：一個規模為n的問題可以轉化為規模比他小的子問題來求解。換言之，f(n)可以通過一個比他規模小的遞推式來求解，在前面的斐波拉契數列這個遞推式就是f(n) = f(n-1) + f(n -2)。一般具有這種結構的問題也可以用遞迴求解，但是遞迴的複雜度太高。
2. 子問題的重疊性：如果用遞迴求解，會有很多重複的子問題，動態規劃就是修剪了重複的計算來降低時間複雜度。但是因為需要儲存中間狀態，空間複雜度是增加了。

其實動態規劃的難點是歸納出遞推式，在斐波拉契數列中，遞推式是已經給出的，但是更多情況遞推式是需要我們自己去歸納總結的。

鋼條切割問題

先看看暴力窮舉怎麼做，以一個長度為5的鋼條為例：

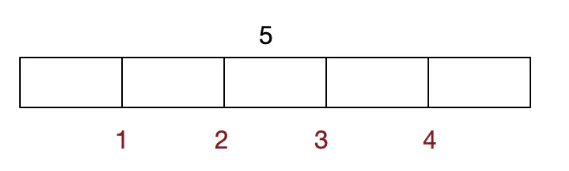
上圖紅色的位置表示可以下刀切割的位置，每個位置可以有切和不切兩種狀態，總共是\(2^4 = 16\)種，對於長度為n的鋼條，這個情況就是\(2^{n-1}\)種。窮舉的方法就不寫程式碼了，下面直接來看遞迴的方法：

遞迴方案

還是以上面那個長度為5的鋼條為例，假如我們只考慮切一刀的情況，這一刀的位置可以是1，2，3，4中的任意位置，那切割之後，左右兩邊的長度分別是：

// [left, right]: 表示切了後左邊，右邊的長度
[1, 4]: 切1的位置
[2, 3]: 切2的位置
[3, 2]: 切3的位置
[4, 1]: 切4的位置

分成了左右兩部分，那左右兩部分又可以繼續切，每部分切一刀，又變成了兩部分，又可以繼續切。這不就將一個長度為5的問題，分解成了4個小問題嗎，那最優的方案就是這四個小問題裡面最大的那個值，同時不要忘了我們也可以一刀都不切，這是第五個小問題，我們要的答案其實就是這5個小問題裡面的最大值。寫成公式就是，對於長度為n的鋼條，最佳收益公式是：

• \(r_n\) : 表示我們求解的目標，長度為n的鋼條的最大收益
• \(p_n\): 表示鋼條完全不切的情況
• \(r_1 + r_{n-1}\): 表示切在1的位置，分為了左邊為1，右邊為n-1長度的兩端，他們的和是這種方案的最優收益
• 我們的最大收益就是不切和切在不同情況的子方案裡面找最大值

上面的公式已經可以用遞迴求解了：

const p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]; // 下標表示鋼條長度，值表示對應價格

function cut_rod(n) {
  if(n === 1) return 1;
  
  let max = p[n];
  for(let i = 1; i < n; i++){
    let sum = cut_rod(i) + cut_rod(n - i);
    if(sum > max) {
      max = sum;
    }
  }
  
  return max;
}

cut_rod(9);  // 返回 25

上面的公式還可以簡化，假如我們長度9的最佳方案是切成2 3 2 2，用前面一種演算法，第一刀將它切成2 7和5 4，然後兩邊再分別切最終都可以得到2 3 2 2，所以5 4方案最終結果和2 7方案是一樣的，都會得到2 3 2 2，如果這兩種方案，兩邊都繼續切，其實還會有重複計算。那長度為9的切第一刀，左邊的值肯定是1 -- 9，我們從1依次切過來，如果後面繼續對左邊的切割，那繼續切割的那個左邊值必定是我們前面算過的一個左邊值。比如5 4切割成2 3 4，其實等價於第一次切成2 7，第一次如果是3 6,如果繼續切左邊，切為1 2 6，其實等價於1 8，都是前面切左邊為1的時候算過的。所以如果我們左邊依次是從1切過來的，那麼就沒有必要再切左邊了，只需要切右邊。所以我們的公式可以簡化為：
\[ r_n = \max_{1<=i<=n}(pi+r_{n-i}) \]
繼續用遞迴實現這個公式：

const p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]; // 下標表示鋼條長度，值表示對應價格

function cut_rod2(n) {
  if(n === 1) return 1;
  
  let max = p[n];
  for(let i = 1; i <= n; i++){
    let sum = p[i] + cut_rod2(n - i);
    if(sum > max) {
      max = sum;
    }
  }
  
  return max;
}

cut_rod2(9);  // 結果還是返回 25

上面的兩個公式都是遞迴，複雜度都是指數級的，下面我們來講講動態規劃的方案。

動態規劃方案

動態規劃方案的公式和前面的是一樣的，我們用第二個簡化了的公式：
\[ r_n = \max_{1<=i<=n}(pi+r_{n-i}) \]
動態規劃就是不用遞迴，而是從底向上計算值，每次計算上面的值的時候，下面的值算好了，直接拿來用就行。所以我們需要一個數組來記錄每個長度對應的最大收益。

const p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]; // 下標表示鋼條長度，值表示對應價格

function cut_rod3(n) {
  let r = [0, 1];   // r陣列記錄每個長度的最大收益
  
  for(let i = 2; i <=n; i++) {
    let max = p[i];
    for(let j = 1; j <= i; j++) {
      let sum = p[j] + r[i - j];
      
      if(sum > max) {
        max = sum;
      }
    }
    
    r[i] = max;
  }
  
  console.log(r);
  return r[n];
}

cut_rod3(9);  // 結果還是返回 25

我們還可以把r陣列也打出來看下，這裡面存的是每個長度對應的最大收益：

r = [0, 1, 5, 8, 10, 13, 17, 18, 22, 25]

使用動態規劃將遞迴的指數級複雜度降到了雙重迴圈，即\(O(n^2)\)的複雜度。

輸出最佳方案

上面的動態規劃雖然計算出來最大值，但是我們並不是知道這個最大值對應的切割方案是什麼，為了知道這個方案，我們還需要一個數組來記錄切割一次時左邊的長度，然後在這個陣列中回溯來找出切割方案。回溯的時候我們先取目標值對應的左邊長度，然後右邊剩下的長度右繼續去這個陣列找最優方案對應的左邊切割長度。假設我們左邊記錄的陣列是：

leftLength = [0, 1, 2, 3, 2, 2, 6, 1, 2, 3]

我們要求長度為9的鋼條的最佳切割方案：

1. 找到leftLength[9], 發現值為3，記錄下3為一次切割
2. 左邊切了3之後，右邊還剩6，又去找leftLength[6]，發現值為6，記錄下6為一次切割長度
3. 又切了6之後，發現還剩0，切完了，結束迴圈；如果還剩有鋼條繼續按照這個方式切
4. 輸出最佳長度為[3, 6]

改造程式碼如下：

const p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]; // 下標表示鋼條長度，值表示對應價格

function cut_rod3(n) {
  let r = [0, 1];   // r陣列記錄每個長度的最大收益
  let leftLength = [0, 1];  // 陣列leftLength記錄切割一次時左邊的長度
  let solution = [];
  
  for(let i = 2; i <=n; i++) {
    let max = p[i];
    leftLength[i] = i;     // 初始化左邊為整塊不切
    for(let j = 1; j <= i; j++) {
      let sum = p[j] + r[i - j];
      
      if(sum > max) {
        max = sum;
        leftLength[i] = j;  // 每次找到大的值，記錄左邊的長度
      } 
    }
    
    r[i] = max;
  }
  
  // 回溯尋找最佳方案
  let tempN = n;
  while(tempN > 0) {
    let left = leftLength[tempN];
    solution.push(left);
    tempN = tempN - left;
  }
  
  console.log(leftLength);  // [0, 1, 2, 3, 2, 2, 6, 1, 2, 3]
  console.log(solution);    // [3, 6]
  console.log(r);           // [0, 1, 5, 8, 10, 13, 17, 18, 22, 25]
  return {max: r[n], solution: solution};
}

cut_rod3(9);  // {max: 25, solution: [3, 6]}

最長公共子序列

上敘問題也可以用暴力窮舉來求解，先列舉出X字串所有的子串，假設他的長度為m，則總共有\(2^m\)種情況，因為對於X字串中的每個字元都有留著和不留兩種狀態，m個字元的全排列種類就是\(2^m\)種。那對應的Y字串就有\(2^n\)種子串, n為Y的長度。然後再遍歷找出最長的公共子序列，這個複雜度非常高，我這裡就不寫了。

我們觀察兩個字串，如果他們最後一個字元相同，則他們的LCS就是兩個字串都去調最後一個字元的LCS再加一，如果他們最後一個字元不相同，那他們的LCS就是X去掉最後一個字元與Y的LCS，或者是X與Y去掉最後一個字元的LCS，是他們兩個中較長的那一個。寫成數學公式就是：

看著這個公式，一個規模為(i, j)的問題轉化為了規模為(i-1, j-1)的問題，這不就又可以用遞迴求解了嗎？

遞迴方案

公式都有了，不廢話，直接寫程式碼：

function lcs(str1, str2) {
  let length1 = str1.length;
  let length2 = str2.length;
  
  if(length1 === 0 || length2 === 0) {
    return 0;
  }
  
  let shortStr1 = str1.slice(0, -1);
  let shortStr2 = str2.slice(0, -1);
  if(str1[length1 - 1] === str2[length2 -  1]){
    return lcs(shortStr1, shortStr2) + 1;
  } else {
    let lcsShort2 = lcs(str1, shortStr2);
    let lcsShort1 = lcs(shortStr1, str2);
    
    return lcsShort1 > lcsShort2 ? lcsShort1 : lcsShort2;
  }
}

let result = lcs('ABBCBDE', 'DBBCD');
console.log(result);   // 4

動態規劃

遞迴雖然能實現我們的需求，但是複雜度是在太高，長一點的字串需要的時間是指數級增長的。我們還是要用動態規劃來求解，根據我們前面講的動態規劃原理，我們需要從小的往大的算，每算出一個值都要記下來。因為c(i, j)裡面有兩個變數，我們需要一個二維陣列才能存下來。注意這個二維陣列的行數是X的長度加一，列數是Y的長度加一，因為第一行和第一列表示X或者Y為空串的情況。程式碼如下：

function lcs2(str1, str2) {
  let length1 = str1.length;
  let length2 = str2.length;
  
  // 構建一個二維陣列
  // i表示行號，對應length1 + 1
  // j表示列號， 對應length2 + 1
  // 第一行和第一列全部為0
  let result = [];
  for(let i = 0; i < length1 + 1; i++){
    result.push([]); //初始化每行為空陣列
    for(let j = 0; j < length2 + 1; j++){
      if(i === 0) {
        result[i][j] = 0; // 第一行全部為0
      } else if(j === 0) {
        result[i][j] = 0; // 第一列全部為0
      } else if(str1[i - 1] === str2[j - 1]){
        // 最後一個字元相同
        result[i][j] = result[i - 1][j - 1] + 1;
      } else{
        // 最後一個字元不同
        result[i][j] = result[i][j - 1] > result[i - 1][j] ? result[i][j - 1] : result[i - 1][j];
      }
    }
  }
  
  console.log(result);
  return result[length1][length2]
}

let result = lcs2('ABCBDAB', 'BDCABA');
console.log(result);   // 4

上面的result就是我們構造出來的二維陣列，對應的表格如下，每一格的值就是c(i, j)，如果\(X_i = Y_j\)，則它的值就是他斜上方的值加一，如果\(X_i \neq Y_i\)，則它的值是上方或者左方較大的那一個。

輸出最長公共子序列

要輸出LCS，思路還是跟前面切鋼條的類似，把每一步操作都記錄下來，然後再回溯。為了記錄操作我們需要一個跟result二維陣列一樣大的二維陣列，每個格子裡面的值是當前值是從哪裡來的，當然，第一行和第一列仍然是0。每個格子的值要麼從斜上方來，要麼上方，要麼左方，所以：

1. 我們用1來表示當前值從斜上方來
2. 我們用2表示當前值從左方來
3. 我們用3表示當前值從上方來

看程式碼：

function lcs3(str1, str2) {
  let length1 = str1.length;
  let length2 = str2.length;
  
  // 構建一個二維陣列
  // i表示行號，對應length1 + 1
  // j表示列號， 對應length2 + 1
  // 第一行和第一列全部為0
  let result = [];
  let comeFrom = [];   // 儲存來歷的陣列
  for(let i = 0; i < length1 + 1; i++){
    result.push([]); //初始化每行為空陣列
    comeFrom.push([]);
    for(let j = 0; j < length2 + 1; j++){
      if(i === 0) {
        result[i][j] = 0; // 第一行全部為0
        comeFrom[i][j] = 0;
      } else if(j === 0) {
        result[i][j] = 0; // 第一列全部為0
        comeFrom[i][j] = 0;
      } else if(str1[i - 1] === str2[j - 1]){
        // 最後一個字元相同
        result[i][j] = result[i - 1][j - 1] + 1;
        comeFrom[i][j] = 1;      // 值從斜上方來
      } else if(result[i][j - 1] > result[i - 1][j]){
        // 最後一個字元不同,值是左邊的大
        result[i][j] = result[i][j - 1];
        comeFrom[i][j] = 2;
      } else {
        // 最後一個字元不同,值是上邊的大
        result[i][j] = result[i - 1][j];
        comeFrom[i][j] = 3;
      }
    }
  }
  
  console.log(result);
  console.log(comeFrom);
  
  // 回溯comeFrom陣列，找出LCS
  let pointerI = length1;
  let pointerJ = length2;
  let lcsArr = [];   // 一個數組儲存LCS結果
  while(pointerI > 0 && pointerJ > 0) {
    console.log(pointerI, pointerJ);
    if(comeFrom[pointerI][pointerJ] === 1) {
      lcsArr.push(str1[pointerI - 1]);
      pointerI--;
      pointerJ--;
    } else if(comeFrom[pointerI][pointerJ] === 2) {
      pointerI--;
    } else if(comeFrom[pointerI][pointerJ] === 3) {
      pointerJ--;
    }
  }
  
  console.log(lcsArr);   // ["B", "A", "D", "B"]
  //現在lcsArr順序是反的
  lcsArr = lcsArr.reverse();
  
  return {
    length: result[length1][length2], 
    lcs: lcsArr.join('')
  }
}

let result = lcs3('ABCBDAB', 'BDCABA');
console.log(result);   // {length: 4, lcs: "BDAB"}

最短編輯距離

這是leetcode上的一道題目，題目描述如下：

這道題目的思路跟前面最長公共子序列非常像，我們同樣假設第一個字串是\(X=(x_1, x_2 ... x_m)\),第二個字串是\(Y=(y_1, y_2 ... y_n)\)。我們要求解的目標為\(r\), \(r[i][j]\)為長度為\(i\)的\(X\)和長度為\(j\)的\(Y\)的解。我們同樣從兩個字串的最後一個字元開始考慮：

1. 如果他們最後一個字元是一樣的，那最後一個字元就不需要編輯了，只需要知道他們前面一個字元的最短編輯距離就行了，寫成公式就是：如果\(Xi = Y_j\)，\(r[i][j] = r[i-1][j-1]\)。
2. 如果他們最後一個字元是不一樣的，那最後一個字元肯定需要編輯一次才行。那最短編輯距離就是\(X\)去掉最後一個字元與\(Y\)的最短編輯距離，再加上最後一個字元的一次；或者是是\(Y\)去掉最後一個字元與\(X\)的最短編輯距離，再加上最後一個字元的一次，就看這兩個數字哪個小了。這裡需要注意的是\(X\)去掉最後一個字元或者\(Y\)去掉最後一個字元，相當於在\(Y\)上進行插入和刪除，但是除了插入和刪除兩個操作外，還有一個操作是替換，如果是替換操作，並不會改變兩個字串的長度，替換的時候，距離為\(r[i][j]=r[i-1][j-1]+1\)。最終是在這三種情況裡面取最小值，寫成數學公式就是：如果\(Xi \neq Y_j\)，\(r[i][j] = \min(r[i-1][j], r[i][j-1],r[i-1][j-1]) + 1\)。
3. 最後就是如果\(X\)或者\(Y\)有任意一個是空字串，那為了讓他們一樣，就往空的那個插入另一個字串就行了，最短距離就是另一個字串的長度。數學公式就是：如果\(i=0\)，\(r[i][j] = j\)；如果\(j=0\)，\(r[i][j] = i\)。

上面幾種情況總結起來就是
\[ r[i][j]= \begin{cases} j, & \text{if}\ i=0 \\ i, & \text{if}\ j=0 \\ r[i-1][j-1], & \text{if}\ X_i=Y_j \\ \min(r[i-1][j], r[i][j-1], r[i-1][j-1]) + 1, & \text{if} \ X_i\neq Y_j \end{cases} \]

遞迴方案

老規矩，有了遞推公式，我們先來寫個遞迴：

const minDistance = function(str1, str2) {
    const length1 = str1.length;
    const length2 = str2.length;

    if(!length1) {
        return length2;
    }

    if(!length2) {
        return length1;
    }

    const shortStr1 = str1.slice(0, -1);
    const shortStr2 = str2.slice(0, -1); 

    const isLastEqual = str1[length1-1] === str2[length2-1];

    if(isLastEqual) {
        return minDistance(shortStr1, shortStr2);
    } else {
        const shortStr1Cal = minDistance(shortStr1, str2);
        const shortStr2Cal = minDistance(str1, shortStr2);
        const updateCal = minDistance(shortStr1, shortStr2);

        const minShort = shortStr1Cal <= shortStr2Cal ? shortStr1Cal : shortStr2Cal;
        const minDis = minShort <= updateCal ? minShort : updateCal;

        return minDis + 1;
    }
}; 

//測試一下
let result = minDistance('horse', 'ros');
console.log(result);  // 3

result = minDistance('intention', 'execution');
console.log(result);  // 5

動態規劃

上面的遞迴方案提交到leetcode會直接超時，因為複雜度太高了，指數級的。還是上我們的動態規劃方案吧，跟前面類似，需要一個二維陣列來存放每次執行的結果。

const minDistance = function(str1, str2) {
    const length1 = str1.length;
    const length2 = str2.length;

    if(!length1) {
        return length2;
    }

    if(!length2) {
        return length1;
    }

    // i 為行，表示str1
    // j 為列，表示str2
    const r = [];
    for(let i = 0; i < length1 + 1; i++) {
        r.push([]);
        for(let j = 0; j < length2 + 1; j++) {
            if(i === 0) {
                r[i][j] = j;
            } else if (j === 0) {
                r[i][j] = i;
            } else if(str1[i - 1] === str2[j - 1]){ // 注意下標，i,j包括空字串，長度會大1
                r[i][j] = r[i - 1][j - 1];
            } else {
                r[i][j] = Math.min(r[i - 1][j ], r[i][j - 1], r[i - 1][j - 1]) + 1;
            }
        }
    }

    return r[length1][length2];
};

//測試一下
let result = minDistance('horse', 'ros');
console.log(result);  // 3

result = minDistance('intention', 'execution');
console.log(result);  // 5

上述程式碼因為是雙重迴圈，所以時間複雜度是\(O(n^2)\)。

總結

動態規劃的關鍵點是要找出遞推式，有了這個遞推式我們可以用遞迴求解，也可以用動態規劃。用遞迴時間複雜度通常是指數級增長，所以我們有了動態規劃。動態規劃的關鍵點是從小往大算，將每一個計算記過的值都記錄下來，這樣我們計算大的值的時候直接就取到前面計算過的值了。動態規劃可以大大降低時間複雜度，但是增加了一個存計算結果的資料結構，空間複雜度會增加。這也算是一種用空間換時間的策略了