本文綜合了幾個相關的維基百科，加了點自己的理解，從比較基礎的向量投影和叉積講起，推匯出羅德里格斯旋轉公式。公式比較繁雜，如有錯誤，歡迎評論區指出。

　　對於向量的三維旋轉問題，給定旋轉軸和旋轉角度，用羅德里格斯（Rodrigues）旋轉公式可以得出旋轉後的向量。另外，羅德里格斯旋轉公式可以用旋轉矩陣表示，即將三維旋轉的軸-角（axis-angle）表示轉變為旋轉矩陣表示。

向量投影（Vector projection）

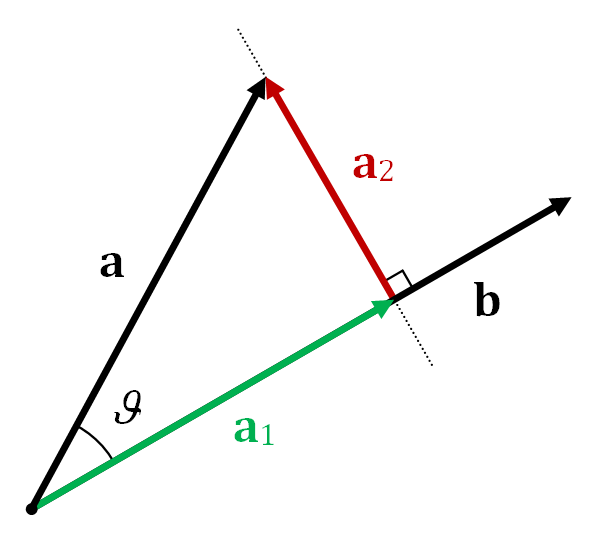
　　向量a在非零向量b上的向量投影指的是a在平行於向量b的直線上的正交投影。結果是一個平行於b的向量，定義為\(\mathbf{a}_1=a_1\hat{\mathbf{b}}\)，其中，\(a_1\)是一個標量，稱為a在b上的標量投影，\(\hat{\mathbf{b}}\)是與b同向的單位向量。\(a_1=\left\Vert\mathbf{a}\right\Vert\cos\theta=\mathbf{a}\cdot \hat{\mathbf{b}}=\mathbf{a}\cdot\frac{\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}\)，其中\(\cdot\)表示點積，\(\left\Vert\mathbf{a}\right\Vert\)表示a的長度，\(\theta\)表示a和b的夾角。標量投影有正負，正負號與夾角\(\theta\)有關。

　　有了向量投影\(\textbf{a}_1\)，向量a可以表示為\(\mathbf{a}=\mathbf{a}_1+\mathbf{a}_2\)，其中\(\mathbf{a}_2\)稱為a from b的vector rejection（沒找到比較官方的翻譯），也即a向正交於b的超平面的正交投影，\(\mathbf{a}_2=\mathbf{a}-\mathbf{a}_1=\mathbf{a}-(\left\Vert\mathbf{a}\right\Vert\cos\theta)\hat{\mathbf{b}}\)。下圖比較清晰地表示出\(\mathbf{a}\)、\(\mathbf{a}_1\)、\(\mathbf{a}_2\)的關係。

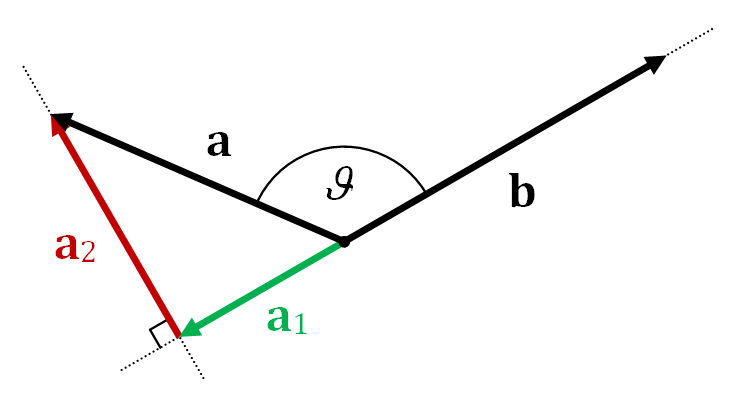
　　當\(90^{\circ}<\theta\le180^{\circ}\)時，向量投影示意圖如圖2所示：

記號

　　向量a在b上的向量投影用加粗的\(\mathbf{a}_1\)表示，標量投影用不加粗的\(a_1\)。有時向量投影和vector rejection分別用\(\mathbf{a}_{\parallel\mathbf{b}}\)和\(\mathbf{a}_{\perp\mathbf{b}}\)表示。

用a和b表示

　　當\(\theta\)未知時，可通過a和b計算得出，\(\cos\theta = \frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert}\)，從而標量投影、向量投影和vector rejection可以分別表示如下：

• 標量投影：
  

  
  \begin{equation}
  a_1=\left\Vert\mathbf{a}\right\Vert\cos\theta=\left\Vert\mathbf{a}\right\Vert\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert}=\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}
  \end{equation}
  

• 向量投影：
  

  
  \begin{equation}
  \mathbf{a}_1=a_1\hat{\mathbf{b}}=\frac{\mathbf{a}\cdot\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}\frac{\mathbf{b}}{\left\Vert\mathbf{b}\right\Vert}=\left(\mathbf{a}\cdot\hat{\mathbf{b}}\right)\hat{\mathbf{b}}=\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\mathbf{b}
  \end{equation}
  

• vector rejection：
  

  
  \begin{equation}
  \mathbf{a}_2=\mathbf{a}-\mathbf{a}_1=\mathbf{a}-\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\mathbf{b}
  \end{equation}
  

叉積

定義

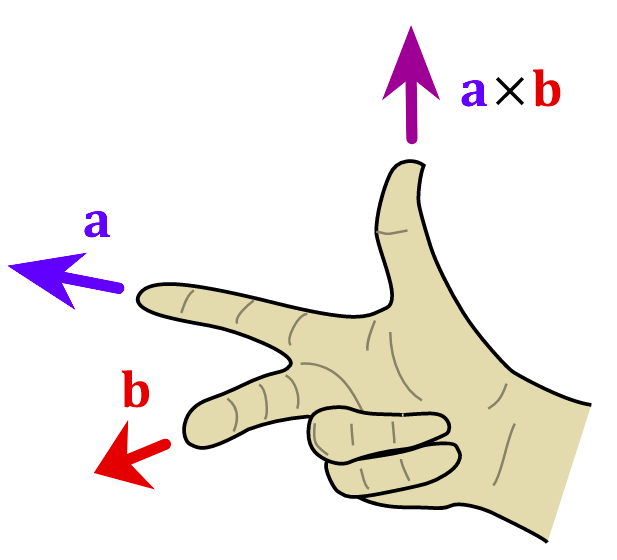
　　叉積（又稱向量積）是三維空間（\(\mathbb{R}^3\)）向量的二元操作，用符號\(\times\)表示，給定兩個線性獨立的向量a和b，叉積\(\mathbf{a}\times\mathbf{b}\)的結果是一個向量，這個向量與a、b都正交，也就是正交於a、b所在的平面。為什麼要強調線性獨立呢，因為非線性獨立的兩個向量（同向或反向）的叉積為\(\mathbf{0}\)。

　　叉積定義為：

\begin{equation}
\mathbf{a}\times\mathbf{b}=\left\Vert\mathbf{a}\right\Vert\left\Vert\mathbf{b}\right\Vert\sin(\theta)\mathbf{n}
\end{equation}

性質

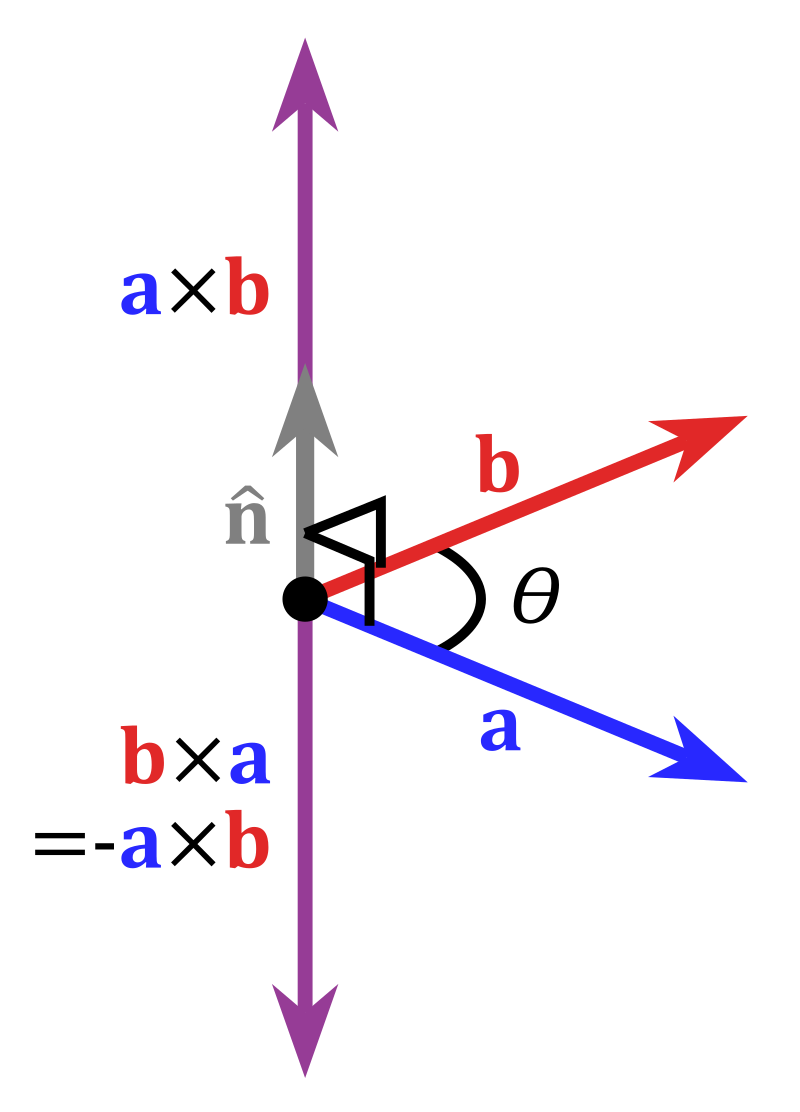
　　右手法則決定了叉積不符合交換律，而符合反交換律，即\(\mathbf{a}\times\mathbf{b}=-\mathbf{b}\times\mathbf{a}\)，如圖4所示：

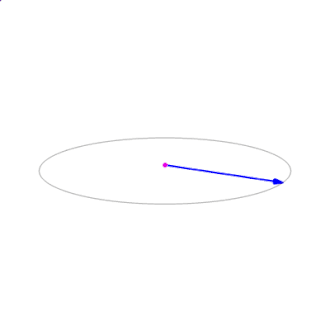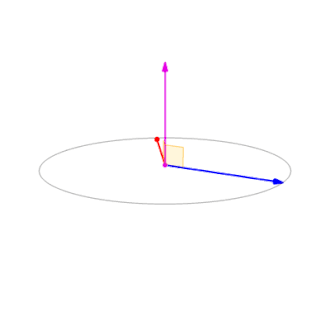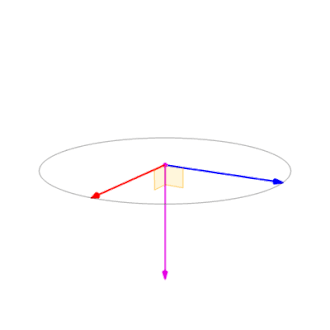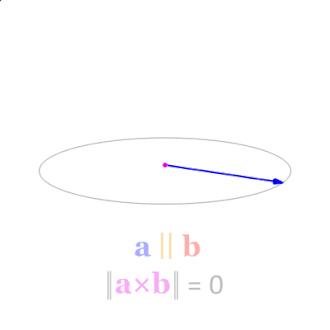
　　由公式也可以看出當a、b的不線性獨立時，即夾角為\(0^\circ\)或\(180^\circ\)時，叉積為零向量\(\mathbf{0}\)。叉積隨夾角\(\theta\)的變化如圖5所示。

　　另外，叉積符合分配律，即\(\mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}\)。如圖6所示，左圖向量b和c都被分解為vector projection和vector rejection兩部分，右圖則解釋了分配律成立的原因，看圖時要注意圖中的平行四邊形和正方形都表示了相等的關係。

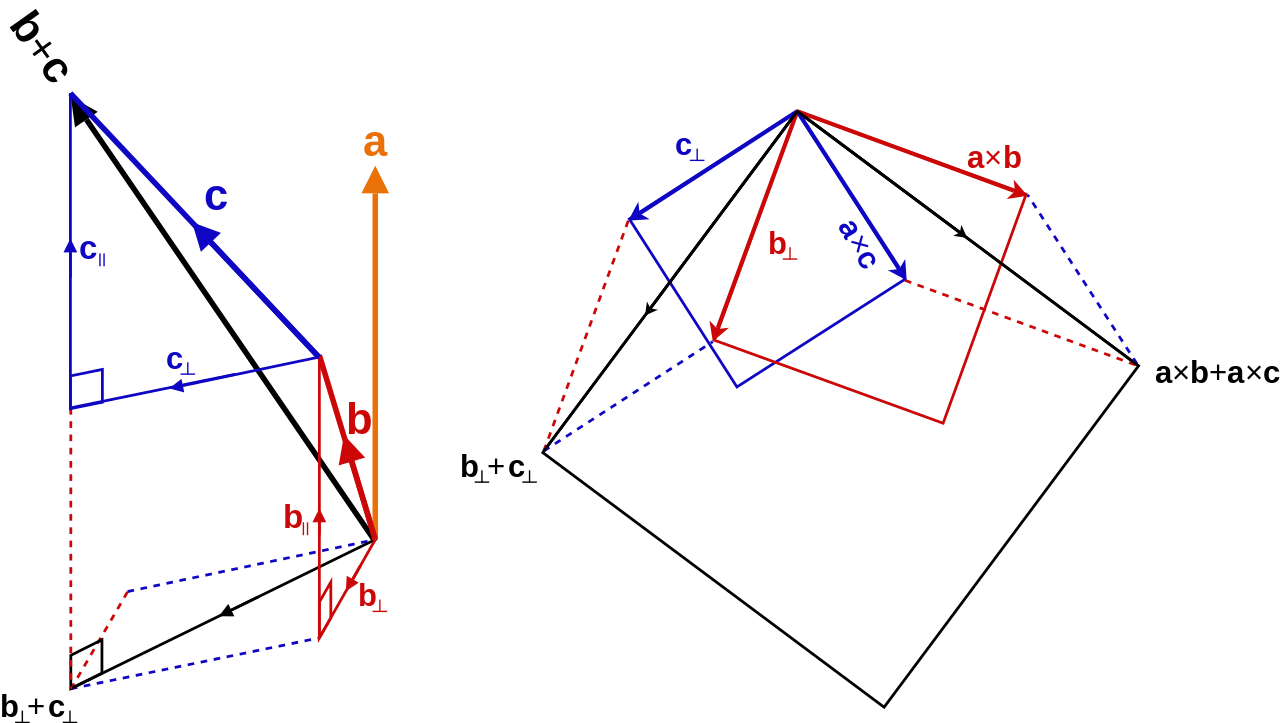
座標表示

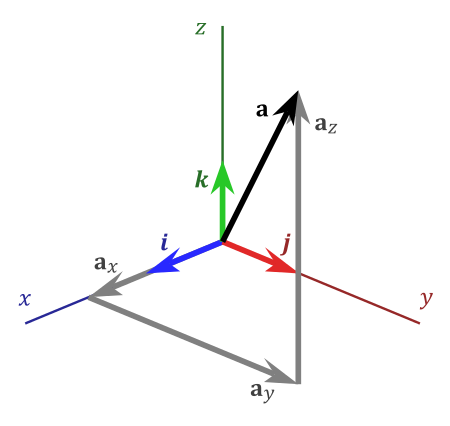
　　考慮右手法則定義的標準三維座標系，三個座標軸\(\mathbf{i}\)、\(\mathbf{j}\)、\(\mathbf{{k}}\)如圖7所示，並滿足以下等式關係：
\[ \mathbf{i}\times\mathbf{j}=\mathbf{k}\\ \mathbf{j}\times\mathbf{k}=\mathbf{i}\\ \mathbf{k}\times\mathbf{i}=\mathbf{j} \]
同樣，由叉積的反交換律可得下面三個等式關係：
\[ \mathbf{j}\times\mathbf{i}=-\mathbf{k}\\ \mathbf{k}\times\mathbf{j}=-\mathbf{i}\\ \mathbf{i}\times\mathbf{k}=-\mathbf{j} \]
由平行向量的叉積為零向量可得：\(\mathbf{i}\times\mathbf{i}=\mathbf{j}\times\mathbf{j}=\mathbf{k}\times\mathbf{k}=\mathbf{0}\)。
　　由圖7也可得，任意一個三維向量都可以表示為三個基向量的線性組合，例如：
\[ \mathbf{a}=a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k}\\ \mathbf{b}=b_1\mathbf{i}+b_2\mathbf{j}+b_2\mathbf{k} \]

　　進而，可以用座標表示叉積運算如下：

\begin{equation} \begin{split} \mathbf{a}\times\mathbf{b}&=(a_1\mathbf{i}+a_2\mathbf{j}+a_3\mathbf{k})\times(b_1\mathbf{i}+b_2\mathbf{j}+b_2\mathbf{k})\\ &=(a_2b_3-a_3b_2)\mathbf{i}+(a_3b_1-a_1b_3)\mathbf{j}+(a_1b_2-a_2b_1)\mathbf{k}\\ &=\left|\begin{array}{cccc} i & j & k \\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array}\right| \end{split} \end{equation}

上式中，將括號展開分別進行叉積推匯出第二個等號，而第三個等號則可通過行列式計算得出。
　　進一步，可將叉積表示為矩陣與向量相乘的形式，由於\(\mathbf{a}\times\mathbf{b}=(a_2b_3-a_3b_2, a_3b_1-a_1b_3,a_1b_2-a_2b_1)\)，則叉積可表示為：

\begin{equation} \begin{split} \mathbf{a}\times\mathbf{b}=\left[\mathbf{a}\right]_\times\mathbf{b}=\left[\begin{array}{cccc} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{array} \right]\left[ \begin{array}{cc} b_1\\b_2\\b_3 \end{array}\right]=\left[\mathbf{b}\right]^T_\times\mathbf{a}=\left[\begin{array}{cccc} 0 & b_3 & -b_2\\ -b_3 & 0 & b_1\\ b_2 & -b_1 & 0 \end{array} \right]\left[ \begin{array}{cc} a_1\\a_2\\a_3 \end{array}\right] \end{split} \end{equation}

其中，\(\left[\mathbf{a}\right]_\times\)（slam14講書上記為\(\mathbf{a}^\wedge\)）表示由向量\(\mathbf{a}\)得到的反對稱矩陣，定義為：

\begin{equation} \begin{split} \left[\mathbf{a}\right]_\times=\left[\begin{array}{cccc} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{array} \right] \end{split} \end{equation}

通過該反對稱矩陣的定義可以將叉積表示為矩陣與向量的乘法。

羅德里格斯旋轉公式

　　考慮\(\mathbf{v}\in\mathbb{R}^3\)的三維旋轉問題，旋轉軸\(\mathbf{k}\)是單位向量，旋轉角為\(\theta\)，按照右手法則（即逆時針）旋轉。則可通過羅德里格斯旋轉公式得出旋轉後的向量\(\mathbf{v}_{rot}\)為：

\begin{equation} \mathbf{v}_{rot}=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{k}\cdot\mathbf{v})\mathbf{k}+\sin\theta\mathbf{k}\times\mathbf{v} \end{equation}

推導過程

　　由上文中向量投影部分的知識我們知道，一個向量\(\mathbf{v}\)可以分解為平行於\(\mathbf{k}\)的分量\(\mathbf{v}_\parallel\)和正交於\(\mathbf{k}\)的分量\(\mathbf{v}_{\perp}\)：

\begin{equation} \mathbf{v}=\mathbf{v}_{\parallel}+\mathbf{v}_\perp \end{equation}

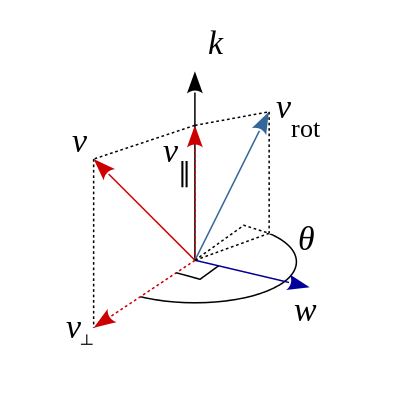
如圖8所示，因為\(\mathbf{k}\)為單位向量，由向量投影部分知識可得

\begin{equation} \mathbf{v}_\parallel=(\mathbf{v}\cdot\mathbf{k})\mathbf{k} \end{equation}

\begin{equation} \mathbf{v}_\perp=\mathbf{v}-\mathbf{v}_\parallel=\mathbf{v}-(\mathbf{k}\cdot\mathbf{v})\mathbf{k}=-\mathbf{k}\times(\mathbf{k}\times\mathbf{v}) \end{equation}

關於上式最後一個等號的推導如下：

　　回顧叉積的知識，\(\mathbf{k}\times\mathbf{v}=\mathbf{k}\times(\mathbf{v}_{\parallel}+\mathbf{v}_\perp)=\mathbf{0}+\mathbf{k}\times\mathbf{v}_\perp=\mathbf{k}\times\mathbf{v}_\perp\)，\(\mathbf{k}\times\mathbf{v}\)可以看做將\(\mathbf{v}_\perp\)以\(\mathbf{k}\)為旋轉軸逆時針旋轉了\(90^\circ\)。正如圖9所示，\(\mathbf{v}\)分解為\(\mathbf{v}_\parallel\)和\(\mathbf{v}_\perp\)，用右手法則不難確定出\(\mathbf{k}\times\mathbf{v}\)的方向，進而不難發現，\(\mathbf{k}\times(\mathbf{k}\times\mathbf{v})\)可以看做將\(\mathbf{v}_\perp\)以\(\mathbf{k}\)為旋轉軸逆時針旋轉了\(180^\circ\)，圖9中的(橢)圓正反映了\(\mathbf{k}\times(\mathbf{k}\times\mathbf{v})\)、\(\mathbf{k}\times\mathbf{v}\)、\(\mathbf{v}_\perp\)三者“大小相等”的關係。最終，可知\(\mathbf{v}_\perp=-\mathbf{k}\times(\mathbf{k}\times\mathbf{v})\)。
　　

　　從圖8還可以看出，v的平行分量\(\mathbf{v}_\parallel\)不會因為旋轉而改變，旋轉後的向量\(\mathbf{v}_{rot}\)的平行分量依然等於\(\mathbf{v}_\parallel\)，即\(\mathbf{v}_{\parallel rot}=\mathbf{v}_\parallel\)。
　　而v的正交分量\(\mathbf{v}_\perp\)在旋轉過程中大小不變，方向會發生變化，即

\begin{equation} \begin{split} &|\mathbf{v}_{\perp rot}|=|\mathbf{v}_\perp|\\ &\mathbf{v}_{\perp rot}=\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}_\perp=\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v} \end{split} \end{equation}

上述第2個等式通過圖9可以得出，將圓看做\(xOy\)座標系平面，\(\mathbf{v}_\perp\)所在的直線看做\(x\)軸，\(\mathbf{k}\times\mathbf{v}\)所在的直線看做\(y\)軸，結合三角函式，很容易用\(\mathbf{v}_\perp\)和\(\mathbf{k}\times\mathbf{v}\)表示出\(\mathbf{v}_\perp\)。

　　到這已經得出羅德里格斯公式了：

\begin{equation} \begin{split} \mathbf{v}_{rot}&=\mathbf{v}_{\parallel rot}+\mathbf{v}_{\perp rot}\\ &=\mathbf{v}_\parallel+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\mathbf{v}_\parallel+\cos\theta(\mathbf{v}-\mathbf{v}_\parallel)+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\cos\theta\mathbf{v}+(1-\cos\theta)\mathbf{v}_\parallel+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\cos\theta\mathbf{v}+(1-\cos\theta)(\mathbf{k}\cdot\mathbf{v})\mathbf{k}+\sin\theta\mathbf{k}\times\mathbf{v} \end{split} \end{equation}

矩陣形式

　　在叉積部分提到過叉積可以表示為矩陣乘向量的形式，類似地，羅德里格斯旋轉公式可以表示為旋轉矩陣乘以向量的形式，\(\mathbf{v}_{rot}=\mathbf{R}\mathbf{v}\)，其中\(\mathbf{R}\)是旋轉矩陣。在slam14講\(^{[4]}\)中的表示如下：
\begin{equation}
\mathbf{R}=\cos\theta\mathbf{I}+(1-\cos\theta)\mathbf{k}\mathbf{k}^T+\sin\theta\mathbf{k}^\wedge
\end{equation}
其中，\(\mathbf{I}\)表示單位矩陣，\(\mathbf{k}\)表示旋轉向量（書中用\(\mathbf{n}\)表示旋轉向量），\(\mathbf{k}^\wedge\)表示由\(\mathbf{k}\)得到的反對稱矩陣。從式(13)不難看出上式，另外，結合式(13)還可以得到下面這個式子：

\begin{equation} \begin{split} \mathbf{v}_{rot}&=\mathbf{v}_{\parallel rot}+\mathbf{v}_{\perp rot}\\ &=\mathbf{v}_\parallel+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\mathbf{v}-\mathbf{v}_\perp+\cos\theta\mathbf{v}_\perp+\sin\theta\mathbf{k}\times\mathbf{v}\\ &=\mathbf{v}+(\sin\theta)\mathbf{k}\times\mathbf{v}+(1-\cos\theta)\mathbf{k}\times\mathbf{k}\times\mathbf{v} \end{split} \end{equation}

從而，得出這個維基百科上的矩陣表示：

\begin{equation} \begin{split} \mathbf{v}_{rot}=\mathbf{R}\mathbf{v}=\mathbf{v}+(\sin\theta)\mathbf{K}\mathbf{v}+(1-\cos\theta)\mathbf{K}^2\mathbf{v} \end{split} \end{equation}

其中，\(\mathbf{R}=\mathbf{I}+(\sin\theta)\mathbf{K}+(1-\cos\theta)\mathbf{K}^2\)，\(\mathbf{K}\)表示由旋轉向量\(\mathbf{k}\)生成的反對稱矩陣。

參考：

[1] Rodrigues' rotation formula
[2] Cross product
[3] Vector projection
[4] 視覺SLAM十四講：從理論到實