引言

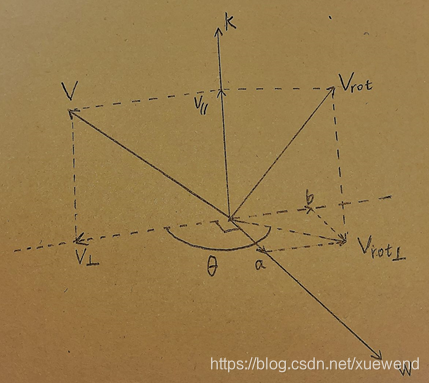
k為單位向量，向量v繞旋轉軸k旋轉Θ得到向量v_rot, 那麼就有下面的旋轉方程使等式成立：
v_rot = Rv
而這個旋轉方程就是羅德里格斯方程：
R=cosΘ I + (1 - cosΘ )kk^τ + sinΘK

下面開始推導：

推導：

向量分解 ,
v _// = (v•k)k (向量點乘得標量，k為單位向量)
v_rot = v_rot⊥ + v _//
v_rot⊥ = a + b
由圖中的向量關係可得：b= cosΘ v_⊥ a=sinΘ k x v

v_rot = v_rot⊥+v_//

= a + b + v_//

= sinΘ k x v + cosΘ v_⊥ + (v • k)k

= sinΘ k x v + cosΘ (v - v_//)+ (v • k)k

= sinΘ k x v + cosΘ (v - (v • k)k)+ (v • k)k

= cosΘ v + (1 - cosΘ )(v • k)k + sinΘ k x v
　　　　　　
所以:
cosΘ v + (1 - cosΘ )(v • k)k + sinΘ k x v

= cosΘ v + (1 - cosΘ )kk^τv + sinΘKv

=( cosΘ I + (1 - cosΘ )kk^τ + sinΘK ) v

=Rv