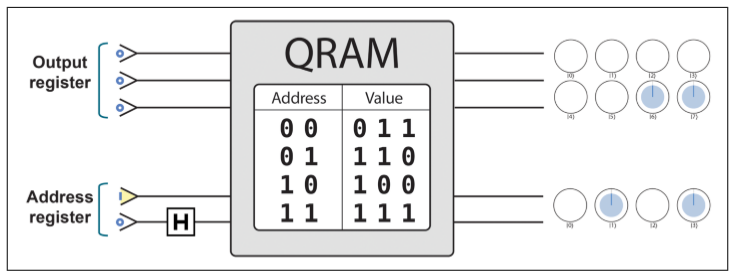
[量子計算機程式設計(一)——QPU程式設計](https://www.cnblogs.com/zmzzzz/p/12323743.html) [量子計算機程式設計(二)——QPU基礎函式](https://www.cnblogs.com/zmzzzz/p/12470253.html) [量子計算機程式設計(三)——量子應用](https://www.cnblogs.com/zmzzzz/p/12493916.html) 量子程式設計一層層搭建，最後是應用層 都到應用了，肯定會涉及資料，本節內容主要包括，量子資料、量子搜尋、量子超級取樣、Shor演算法、量子機器學習。 ### 真實資料 和資料有關的討論一般圍繞在兩個方面，儲存和表示。 #### QRAM 本書沒有討論QRAM如何製造，只是提了用法。  和普通的QRAM有一個重要區別，地址也可以是疊加態。 #### 表示 **小數：**我們可以借鑑經典的手法，就像經典裡面如何表達浮點數的一樣，我們也這樣來表述量子的小數，$Q_{n.m}$n位的資料，其中m位是小數，（n-m）位是整數。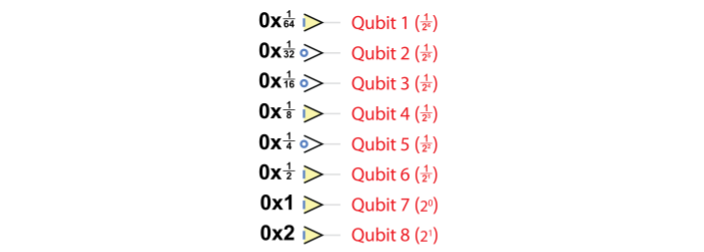  **向量：** [0,1,2,3]這個向量要怎麼表示？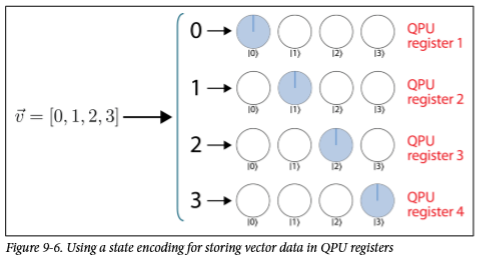 最基礎的：  很容易理解，但是也很浪費空間，沒有用到量子自身的特性。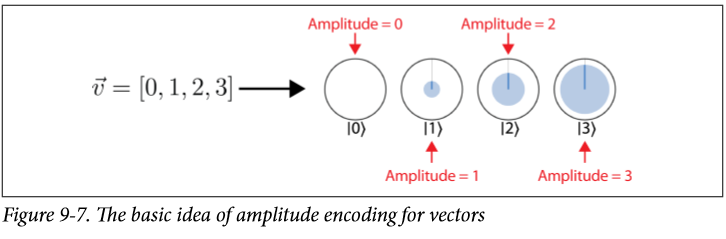 **amplitude encoding for vectors：**  這個就利用了量子的性質，不過他也有自己的侷限性： - 量子疊加態基本就是 unREADable 的 - 因為概率需要歸一化，所以他能表示的態也需要歸一化 **矩陣：** 整體思路是用opertate來表示矩陣： 不過這裡有兩個限制：operator只能unitary的，矩陣不僅不一定是unitary，都不一定是hermitian的。解決方案如下： 不是hermitian的矩陣，可以構建成hermitian，通過 $H=\left[\begin{array}{ll}0 & X \\ X^{\dagger} & 0\end{array}\right]$ 1. Deconstruct $H=H_{1}+\ldots H_{n}$ 把H分解成更容易模擬的hermitian（也就是更容易執行第二步） 2. Simulate components $U=\exp (-i H t)$ 操作只有unitary的操作，但是矩陣可以把他們聯絡到一起 3. Reconstruction 把得到的U乘起來，因為H是在指數上分解的，所以這裡直接乘起來就可以 ### 量子搜尋Quantum Search (QS) Phase Logic ，我們不僅可以改變他們的0或者1，還可以通過01來改變數子態的相位，就像這樣：  相位邏輯和其他邏輯最大的區別就是他把操作結果隱藏到了unreadable的相位裡，通過改變疊加態裡的相位，我們可以在一組暫存器裡標記很多的態，並且還能通過AA之類的方法提取出來。 輸入值還是那些量子態，輸出值則被編碼到了相對相位裡。 那麼這些是怎麼完成的呢？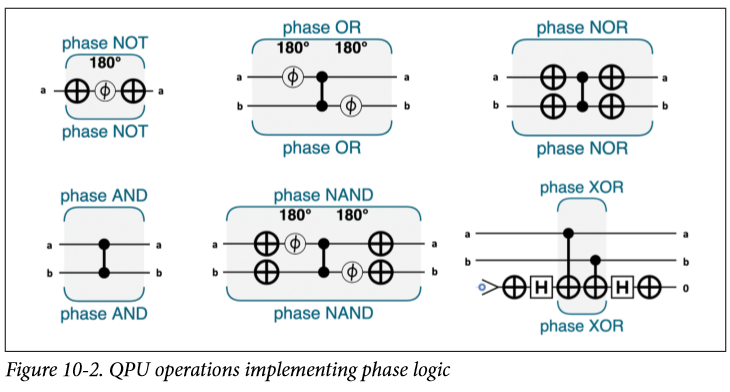簡單的相位邏輯的元件：  所以這個有什麼用？ 圍觀一個小公主找國王爸爸要禮物的例子： 小公主想要一隻小貓咪，爸爸就給了他兩個盒子，盒子A說：至少有一個盒子有貓咪，盒子B說：另一隻盒子有老虎。 爸爸又說，這兩個盒子要麼同時為真，要麼同時為假。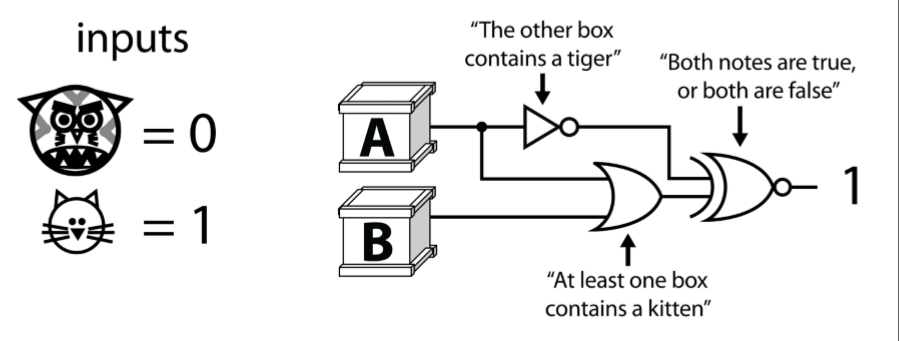 於是我們的小公主殿下搞出了這麼一個數字邏輯：  這樣，跑把四種可能性都跑一遍，輸出為1就滿足了邏輯。 但是爸比就是很喜歡為難他的小可愛，他給公主提出一個要求，這個裝置只能跑一次。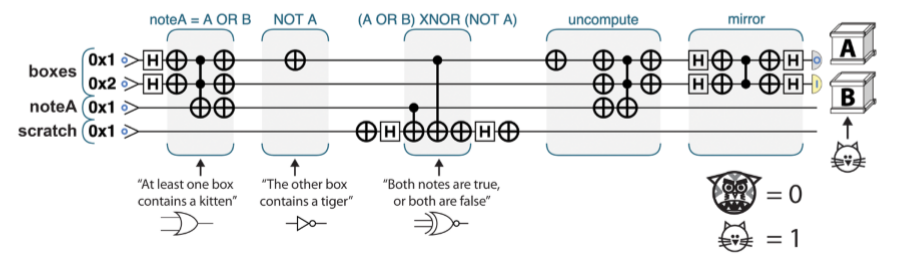 於是小公主就搞了一個量子版本：  首先，用量子的把實驗跑一遍，相對相位上把答案翻轉，然後做實驗的逆操作（所有的量子操作都是可逆的），現在答案就寫在$|00\rangle,|01\rangle|10\rangle|11\rangle$的相對相位裡，再grover把他們找到。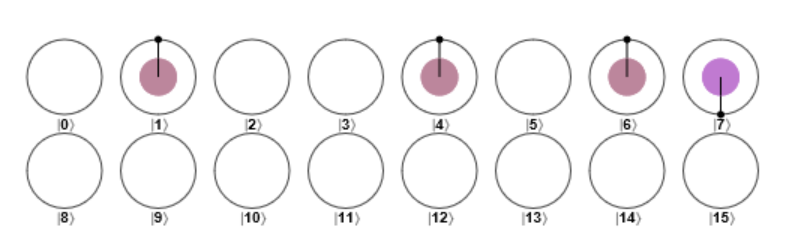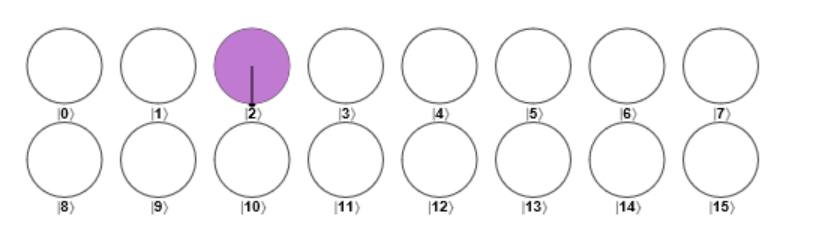 實驗在這裡，https://oreilly-qc.github.io/?p=10-2 把答案翻轉後的狀態：  把答案 uncompute後：  Grover mirror 後：  ### 量子超取樣 超取樣是什麼？ 簡單的說，這是抗鋸齒的一種方法，電腦顯示的圖片由畫素組成，一條線如果不是完全水平或者豎直，那麼表現出來就會有鋸齒，超取樣就是在畫素內部的多個例項處（而不是像正常情況一樣在中心處）獲取顏色樣本，然後計算平均顏色值。通過以比顯示的影象高得多的解析度渲染影象，然後使用多餘的畫素進行計算將其縮小到所需的大小，以此達到目的。 這項任務，我們執行並行處理（計算與場景互動的許多光線的結果），但最終僅需要結果的總和，而不是單個結果本身。（聽起來就可以量子加速） 那麼量子處理器在這裡能做些什麼嗎？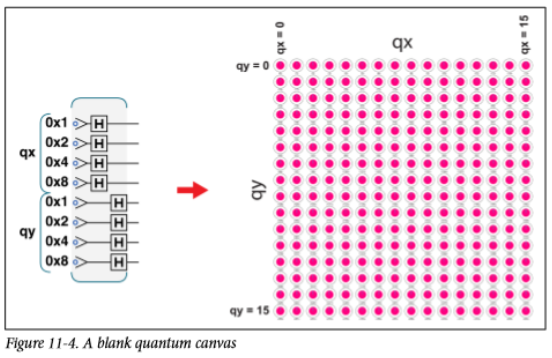  不過首先，在應用QSS之前，我們要知道如何用量子暫存器來表示影象。  這樣就擁有一張畫布，我們可以通過相位翻轉來改變他們的顏色，我們在上面施加的操作就是畫筆。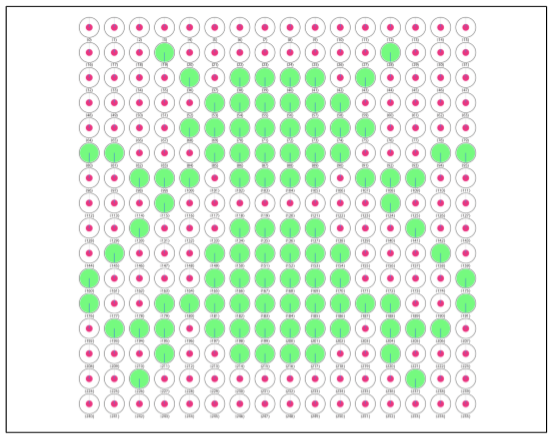  如果想要畫曲線怎麼辦：https://oreilly-qc.github.io/?p=11-2 這是一個畫了曲線的例子。 現在我們來討論超級取樣，對於每個圖塊，我們要估計已被相位翻轉的子畫素的數量。在黑白子畫素（為我們表示為翻轉或非翻轉相位）的情況下，這使我們能夠為每個最終畫素獲取一個代表其原始組成子畫素強度的值。 此問題與前面“多個翻轉項”中的“量子和估計”問題完全相同。要使用量子和估計，我們僅將實現繪製指令的量子程式視為用於翻轉子程式的幅度放大量子程式。將其與第7章中的量子傅立葉變換相結合，可以近似估算每個圖塊中翻轉的子畫素的總數。 不過這樣得到值不是確定的翻轉的數目，我們需要將這個值和look up table結合著來看。  如果還在考慮顏色問題，那就是RGB各來一張圖就好。 ### Shor演算法 因數分解究竟在做什麼，大家可以看一眼這個 [因數分解演算法、週期查詢演算法（簡化）](https://www.cnblogs.com/zmzzzz/p/11290227.html) 預設大家看完有了大概瞭解，現在來看一個具體例子：因數分解15=3*5 程式碼是簡單的呼叫 ``` var N = 15; // The number we're factoring var precision_bits = 4; // See the text for a description of this var coprime = 2; // For this QPU implementation, this must be 2 var result = Shor(N, precision_bits, coprime); ``` 整個過程一共有八步，•Steps 1–4製備 $a^x mod(N)$ 的疊加態，Steps 5–6 量子傅立葉找到週期 Steps 7–8 拿到週期後計算因數 - Step 1: Initialize QPU Registers - Step 2: Expand into Quantum Superposition  前面兩個步驟結束後就是紅色箭頭這裡，現在量子態的狀態如下：  - 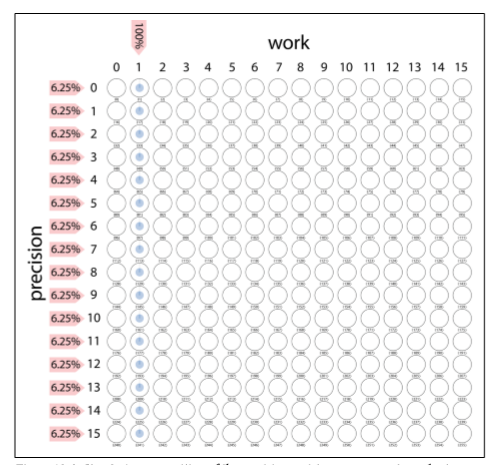Step 3: Conditional Multiply-by-2 這一步是用來計算$2^x$，任何的二進位制暫存器都可通過簡單的移位實現2的乘積（或者實際上是2的任何冪）。在我們的例子中，每個量子位都與下一個最高加權位置交換。需要注意的是我們將只使用精度暫存器的兩個最低權重的量子位來表示x的值（這意味著x可以取值0、1、2、3）,線路為圖上iter0 - Step 4: Conditional Multipy-by-4 線路為圖上iter1，目前我們已經得到了$a^x$,對於我們考慮過的特定示例，我們的電路設法自動處理模數。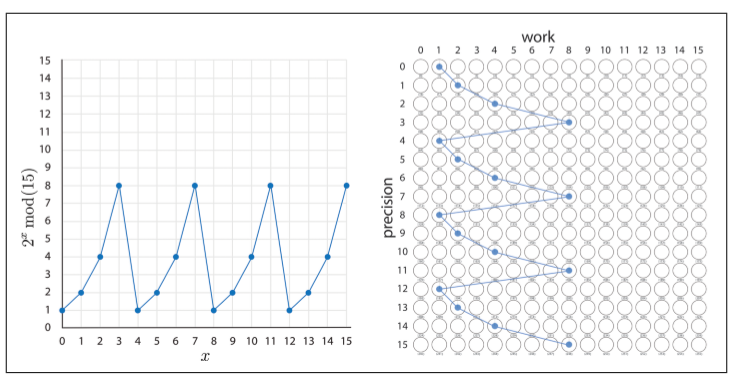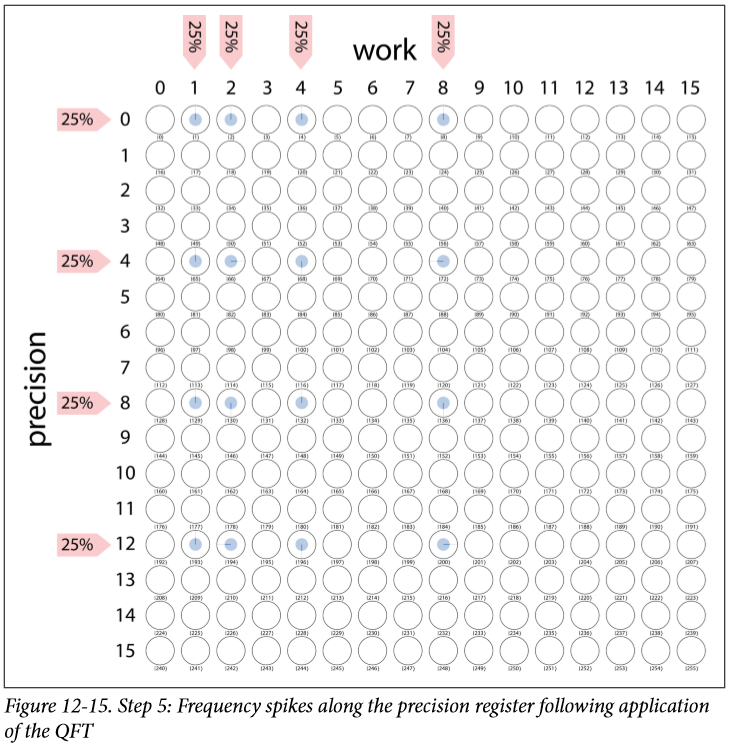 乘2和乘4後量子態的狀態如下：   - Step 5: Quantum Fourier Transform  - Step 6: Read the Quantum Result 測量，我們測量的結果可能是0、4、8、12中的任意一個，他們是等概率25% - Step 7: Digital Logic ``` function ShorLogic(N, repeat_period, coprime) { // Given the repeat period, find the actual factors var ar2 = Math.pow(coprime, repeat_period / 2.0); var factor1 = gcd(N, ar2 - 1); var factor2 = gcd(N, ar2 + 1); return [factor1, factor2]; } ``` 把4丟到這裡面去算，得到的結果是3，5 - Step 8: Check the Result ### 量子機器學習 在這裡我們將要介紹三種QML應用：線性方程組的求解，量子主成分分析和量子支援向量機。 #### [HHL](https://arxiv.org/abs/0811.3171)解線性方程 線性方程很容易變成矩陣乘法的形式$\overrightarrow{\mathbf{A}} \vec{x}=\vec{b}$ ，求解線性方程也就是$\vec{x}=\mathbf{A}^{-1} \vec{b}$ 而HHL提供了一種比共軛梯度下降法更快地方式來找矩陣的逆。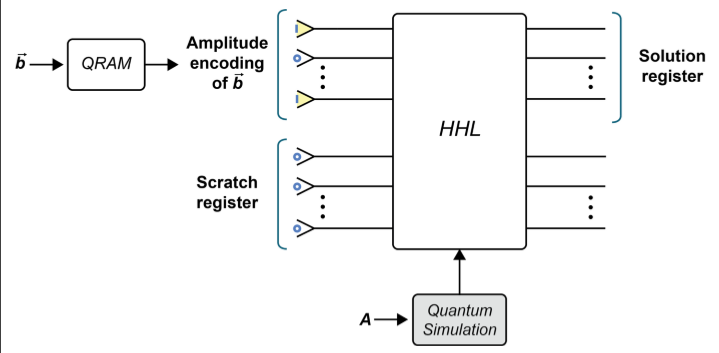  Scratch register 也就是輔助位元包含由HHL中的各種基元使用的許多臨時量子位，所有臨時量子位均以“ 0”狀態準備。因為HHL處理定點（或浮點）資料並且涉及非平凡的算術運算（例如取平方根），所以我們需要大量的臨時qubit。即使最簡單的情況，這也使得HHL難以模擬。 當然如果我們得到了疊加態$|x\rangle$，也不是裡面每一個數據都能讀出來，但是在有的情況下，我們並不需要裡面的每一個值，比如： - 我們可能不需要$|x\rangle$的每個分量的值，而是他們平均值或者和 - 或者我們只想要比較一下看是否等於 - 或者$|x\rangle$只是程式下一部分的輸入 這個演算法的時間複雜度是$O\left(x^{2} s^{2} \epsilon^{-1} \log n\right)$ HHL演算法適合於求解由稀疏，條件良好的矩陣表示的線性方程組。 那具體HHL又是怎麼做的呢是怎麼做到的？ HHL的靈感來自特徵值分解來獲得矩陣逆的資訊，一個栗子： $$A=\left|\begin{array}{ll} 2 & 2 \\ 2 & 3 \end{array}\right|, \quad \vec{z}=\left|\begin{array}{l} 1 \\ 0 \end{array}\right|$$ A的特徵向量為$v_1 = [−0.7882,0.615]$ and $v_2 = [−0.615, −0.788]$,對應的特徵值為 λ1 = 0.438 and λ2 = 4.56， 那麼，在特徵基的表示下，我們可以把z改寫成 [−0.788, −0.615]，因為$\vec{z}=-0.788 \vec{v}_{1}-0.615 \vec{v}_{2}$ 而A可以改寫成：$\Lambda=\left[\begin{array}{cc}0.438 & 0 \\ 0 & 4.56\end{array}\right]$ 現在求逆就很容易了，$\mathbf{A}^{-1}=\left[\begin{array}{cc}\frac{1}{0.438} & 0 \\ 0 & \frac{1}{4.56}\end{array}\right]=\left[\begin{array}{cc}2.281 & 0 \\ 0 & 0.219\end{array}\right]$ 那麼，$\vec{x}=\left[\begin{array}{ccc}\frac{1}{\lambda_{1}} & - & 0 \\ \vdots & \ddots & \vdots \\ 0 & - & \frac{1}{\lambda_{n}}\end{array}\right]\left[\begin{array}{c}\dot{b}_{1} \\ \vdots \\ \tilde{b}_{n}\end{array}\right]=\left[\begin{array}{c}\frac{1}{\lambda_{1}} \dot{b}_{1} \\ \vdots \\ \frac{1}{\lambda_{n}} \dot{b}_{n}\end{array}\right]$  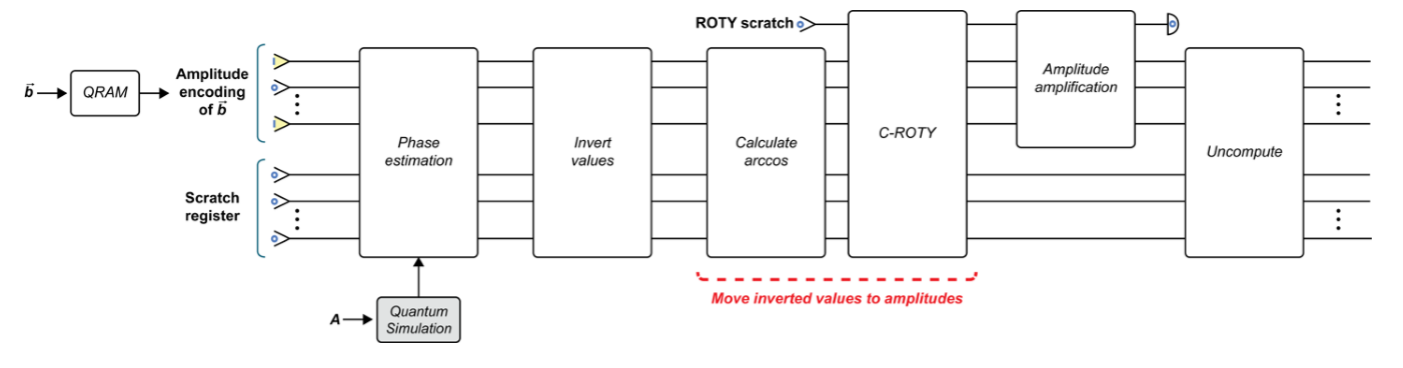1. Quantum simulation, QRAM, and phase estimation 2. Invert values 3. Move inverted values into amplitudes 4. Amplitude amplification 5. Uncompute #### 量子主成分分析 在量子之前，先了解一下什麼是PAC，PCA通常用作預處理步驟，可以將一組輸入的特徵轉換為新的、不相關的集合。 PCA產生的不相關功能可以根據它們編碼的資料差異量進行排序。通過僅保留其中一些新功能，PCA通常被用作降維技術，僅保留前幾個主要成分，可以在儘可能保留差異的情況下減少所需處理的資料量。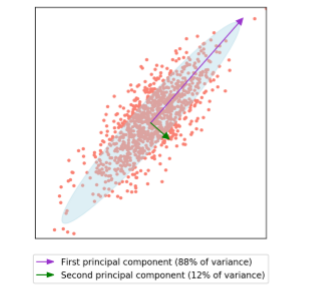 一個簡單例子：  我們一般通過找到該協方差矩陣$\sigma=\frac{1}{n-1} \mathbf{X}^{T} \mathbf{X}$的特徵分解來給出主成分，特徵向量對應於主成分方向，而每個關聯的特徵值均與沿該主成分的資料方差成比例。 其中PCA中計算上最複雜的步驟是執行協方差矩陣的特徵分解。 既然又是特徵分解，那麼我們可能覺得以下行為是有幫助的： - 將資料的協方差矩陣表示為QPU操作。 - 對此QPU操作執行相位估計，以確定其特徵值。 但是這同樣也有問題： - Quantum simulation with σ 協方差矩陣很少能滿足量子模擬技術的稀疏性要求，因此我們需要一種不同的方法來找到σ的QPU運算表示。 - Input for phase estimation 相位估計有兩個輸入暫存器，我們必須使用其中之一來指定要為其關聯本徵相位（並由此獲得本徵值）的本徵態。但是知道σ的任何特徵向量正是我們要使用QPCA解決的問題的一部分。（HHL中可以解決是因為我們有$|b\rangle$） 解決方案： - 用mini-SWAP來改變矩陣的稀疏性，具體見 https://arxiv.org/abs/1307.0401 - σ的密度算符表示正好是我們相位估計的輸入，如果這樣的話，輸出就正好是編碼了的特徵值。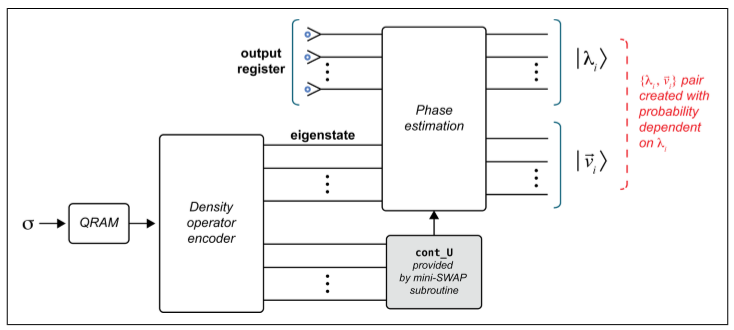  #### 量子支援向量機 支援向量機的主要目的是找到一個超平面，把左右兩類資料給隔開，並且儘可能的，讓這個平面離兩邊資料都遠遠的。 通過對偶問題轉換，我們可以把SVM問題變成最小二乘優化問題。 變成這個問題後，我們的問題就又一次變成如何把這個現有的問題塞到HHL的接替框架