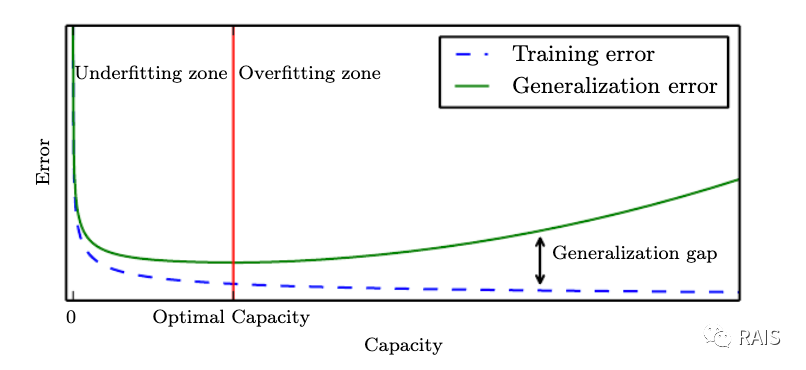
- 本文首發自公眾號：[RAIS](https://ai.renyuzhuo.cn/about) ## ​前言 本系列文章為 [《Deep Learning》](https://ai.renyuzhuo.cn/books/DeepLearning) 讀書筆記，可以參看原書一起閱讀，效果更佳。 ## 構建複雜的機器學習演算法 上一篇文章中我們介紹了什麼叫做機器學習演算法極其具體的定義和所關心的問題，比較簡單，接下來的文章我們將介紹一些設計學習演算法的基本準則。 ### 誤差 - 泛化：機器學習的目的是在新的輸入上具有良好的表現，而不是已有的資料，這很好理解，在新的資料上表現良好的能力叫做 **泛化**。 在機器學習中，總是存在誤差的，百分之百的確定的事件已經不是機器學習研究的範圍了。既然如此，就一定存在誤差，訓練過程在訓練集上誤差稱作 **訓練誤差**，泛化後的在新的輸入上的誤差稱為 **泛化誤差** 或 **測試誤差**。我們都希望誤差儘可能的小，並且相比較而言泛化誤差減小更重要（畢竟解決問題才是最重要的）。 這裡會遇到一個問題就是我們往往只能得到訓練資料集，沒有什麼好的辦法提前獲取模型交付生產環境後所新輸入的資料，針對這樣的問題，我們往往在收集統計訓練資料時，儘量接近實際生產環境，並且假設資料之間是 **獨立同分布** 的，稱為 **資料生成分佈**，基於這樣的原因，我們會假設訓練誤差和測試誤差兩者的期望是一樣的。因此我們針對資料集，具體的做法就會是先儘可能的減小 **訓練誤差**，讓模型在已有的資料上表現良好，然後再儘可能減小 **測試誤差** 與訓練誤差之間的差距，這樣就會得到一個測試誤差較低的模型。 ### 欠擬合和過擬合 上面描述的過程中，會遇到兩個問題，過擬合和欠擬合。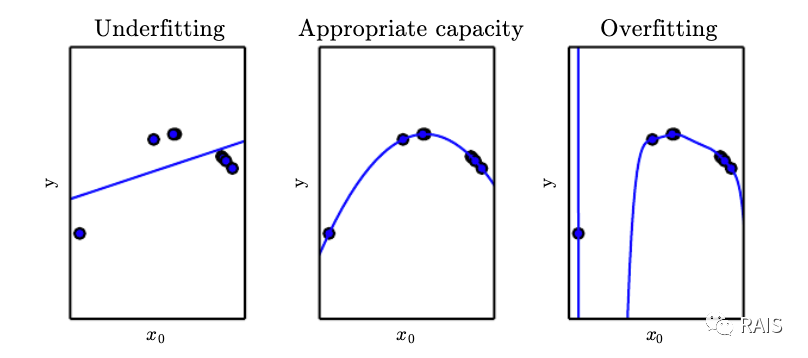 針對訓練集，如果訓練出的模型類似於將每一個訓練集的資料對映到其結果上，訓練誤差幾乎為 0，但是這樣的網路關注了訓練集中的每一個數據的每一個細節，甚至極其特殊的細節，本應該被忽略，卻由於過度追求訓練誤差而被放大了，這是不可取的，這樣訓練出的網路處於過擬合狀態，對新的輸入，尤其是包含特殊細節的輸入，會導致其結果不夠準確，會導致過擬合。 另外一種情況是訓練出的網路針對訓練集中的特徵點訓練不充分，沒有抓住儘可能多的特點，也會導致網路訓練的不夠，處於欠擬合狀態。 ### 容量 網路中模型節點的引數多少，代表著擬合各種函式的能力，稱作 **容量**，節點越多，所關注的網路的特徵就越多，過多會導致過擬合，過少會導致欠擬合，因此控制網路的容量就很重要。 一種控制容量的演算法是選擇 **假設空間**，具體的實現就是選擇解決方案的函式集。比如線性迴歸演算法將關於其輸入的所有線性函式作為假設空間，廣義線性迴歸的假設空間包含多項式函式，而不僅僅是線性函式。在實際的情況中，找到最合適的擬合函式容量比較難，往往是找到一個大致的容量。  - 表示容量：我們可以從哪些函式族中選擇擬合函式； - 有效容量：有可能小於表示容量，基本達到最初的目標，只找到了一個效果還不錯但並非完全完美的擬合函式。 ### 一些概念 - 奧卡姆剃刀：在同樣能夠解釋已知觀測的現象中，應該挑選最簡單一個（像不像物理上追求大一統的理論）。 - VC 維：Vapnic-Chervonenkis Dimension，用來度量容量。如二維假設空間，如果平面上有兩個點，分成兩類，可能有四種情況；三個點有八種情況；四個點有十四種情況，這樣整個平面就分為了相應的部分，無窮的假設點分為了有限的部分。 - 非引數模型：引數模型學習的函式在觀測到新資料前，引數向量的分量個數是有限且固定的，非引數模型沒有這些限制。 ### 最近臨近迴歸 線性迴歸的做法是訓練出固定長度的向量作為權重，最近臨近演算法則不同，而是儲存了所有的訓練集中的資料，所需要測量的測試點分別與訓練集中的點計算距離，認為距離最近的點就和測試點所在同一個類別中，返回同一個迴歸目標。  ### 貝葉斯誤差 也稱 **貝葉斯錯誤率**，應用貝葉斯分類規則分類器的錯誤率，貝葉斯分類規則在最小分類錯誤率上是最優的，因此在所有分類問題中，貝葉斯誤差是一個分類器對某個類別所能達到的最低的分類錯誤率。 ### 沒有免費午餐定理 在所有可能的資料生成分佈上平均後，每個分類演算法在未事先觀測的點上都有相同的錯誤率；換一句話說，沒有任何一種機器學習演算法是適用於所有情況的；再換一句話說，在某些問題上演算法 A 比演算法 B 更好，則一定有另外一些問題，演算法 B 比演算法 A 更好。這告訴我們不要去試圖找到一個大一統的演算法理論，而應該根據實際問題去尋找相應的最優的演算法。 ### 正則化 這個問題真的是太複雜了，在本書這種級別的書，在後面有一整章來討論這個問題，非常重，因此很幸運在這裡可以簡單的先進行簡單瞭解，在後面的文章中詳細介紹。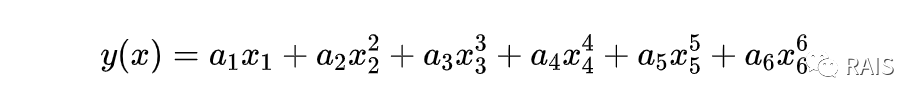 在上面的過擬合的圖中，也在本篇文章的第一個圖，通過過擬合的曲線，我們可以想一下究竟是什麼樣的函式能是這樣的曲線，一定是這個函式好多項，其中變數的次數非常高，例如這樣子的，當然這是隨便一個例子，並不一定完全是這個圖的影象：  對於這個還算簡單的問題，用這麼複雜的函式去擬合，有點過於追求擬合程度了，過猶不及，這不好。怎麼辦呢，假設後面四項的係數 a 接近於 0，是不是可以後面這些項對於整個函式來說貢獻的值就微乎其微了，則這個函式退化為二次函式，這是我們認為擬合程度最好的情況，這就是一種正則化的方法。在後續的文章中還會介紹大量正則化的形式。總結 欠擬合和過擬合是常見機器學習中的擬合不好的情況，上面介紹了相關內容。 - 本文首發自公眾號：[RAIS](https://ai.renyuzhuo.cn