R與金錢遊戲:美股與ARIMA模型預測
阿新 • • 發佈:2020-04-02
似乎突如其來,似乎合情合理,我們和巴菲特老先生一起親見了一次,又一次,雙一次,叒一次的美股熔斷。身處歷史的洪流,渺小的我們會不禁發問:那以後呢?還會有叕一次嗎?於是就有了這篇記錄:利用ARIMA模型來預測美股的走勢。
#### 1. Get Train Dataset and Test Dataset
本例子簡單地以2020年第一季度的道指的收盤價為資料集(資料來源雅虎財經),將前面95%的資料用作本次預測的訓練集,後面5%的資料用作本次預測的測試集。 ```r library(quantmod) stock <- getSymbols("^DJI", from="2020-01-01", from="2020-03-31", auto.assign=FALSE) names(stock) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted") stock <- stock$Close stock <- na.omit(stock) train.id <- 1: (0.95*length(stock)) train <- stock[train.id] test <- stock[-train.id] ``` #### 2. Stationarity Test
由於ARIMA預測要求輸入資料為平穩時間序列。如果輸入資料為非平穩時間序列,則需要對資料進行平穩化處理。識別資料集是否為平穩時間序列,本例子用了兩種方法:1)簡單粗暴的觀察法;2)白噪聲檢驗。 其實對於多次熔斷向下再向下的道指來說,撇開各種觀察和檢驗的方法,我們都知道他一定是非平穩時間序列了。下面兩種方法就是打個版:當我們遇到不太明顯的時間序列時可以怎麼做? ###### 2.1 Observational Method 下圖斷崖式下降的曲線表明訓練集為非平穩時間序列。 ```r library(ggplot2) library(scales) plot<-ggplot(data=train) + geom_line(aes(x=as.Date(Index), y=Close), size=1, color="#0072B2")+ scale_x_date(labels=date_format("%m/%d/%Y"), breaks=date_breaks("2 weeks"))+ ggtitle("Dow Jones Industrial Average") + xlab("")+ theme_light() print(plot) ``` 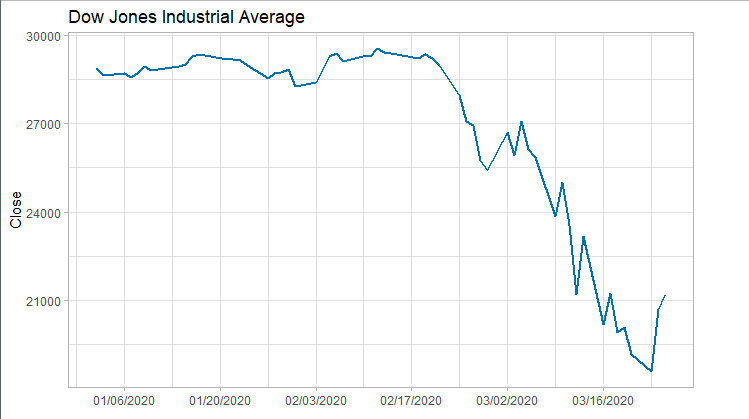 ###### 2.2 Ljung‐Box Statistics Test 利用 Ljung–Box test 得到 p-value = 2.2e-16 < 0.05, 由此拒絕時間序列為白噪聲的假設。 ```r Box.test(train, lag=1, type = "Ljung-Box") ``` #### 3. Differencing
上述我們可知本訓練集為非平穩時間序列,所以我們利用差分對它進行平穩化處理。對訓練集分別進行一階差分和二階差分後,從下圖其實並不能很容易看出一階差分以及二階差分是否為平穩序列。於是我們對其進行了ADF檢驗。從檢驗結果可知: 原序列:p-value = 0.5336 > 0.05,拒絕它是平穩序列的假設; 一階差分:p-value = 0.4495 > 0.05,拒絕它是平穩序列的假設; 二階差分:p-value = 0.01 < 0.05,接受它是平穩序列的假設。 所以我們將利用其二階差分序列進行ARIMA預測。 ```r library("tseries") train.diff1 <- diff(train, lag = 1, differences = 1) train.diff2 <- diff(train, lag = 1, differences = 2) adf.test(train) adf.test(na.exclude(train.diff1)) adf.test(na.exclude(train.diff2)) ``` 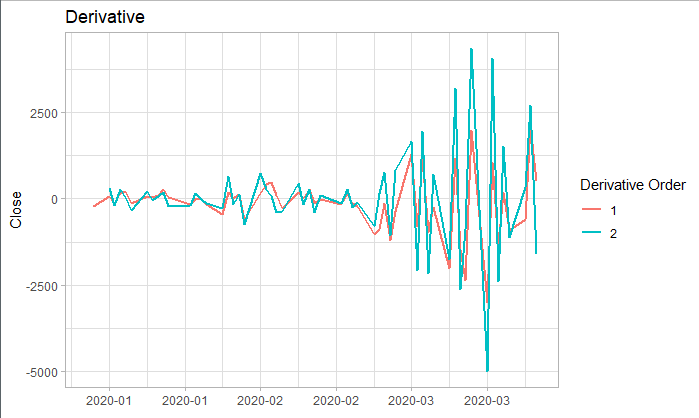 #### 4. ARIMA Model
###### 4.1 Choosing the order 當我們確定用二階差分序列進行預測後,則需要對模型進行定階。如下圖所示,對於ACF,滯後1-2階在2倍標準差外,所以q=2;對於PACF,同樣也是滯後1-2階都在2倍標準差外,所以p=2,所以將會選擇模型ARIMA(2,2,2)。 ```r acf <- acf(na.omit(train.data.diff2$Close), plot=TRUE) pacf <- pacf(na.omit(train.data.diff2$Close), plot=TRUE) ``` 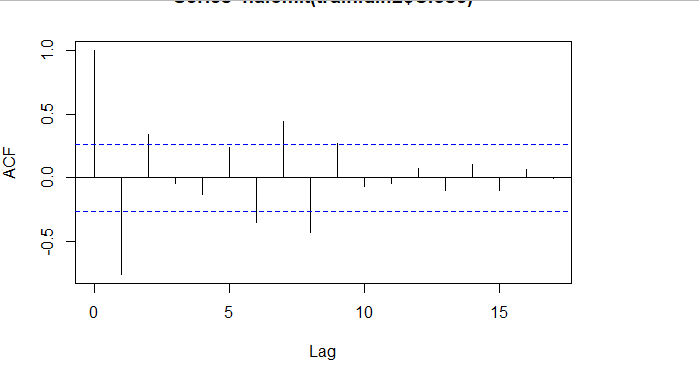 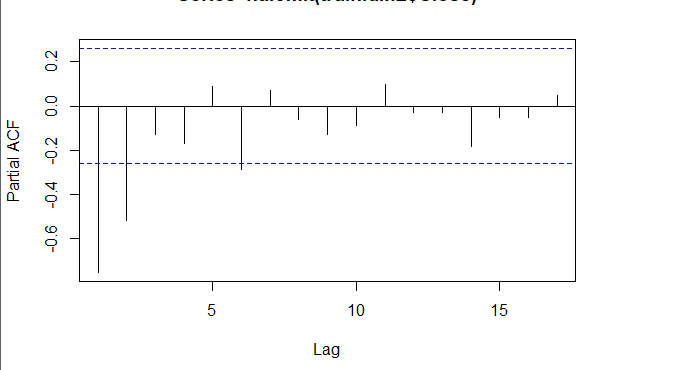 為了保證選擇的模型是最優的,建議可以多選擇接近的模型,然後根據AIC準則或者BIC準則選取最優的模型。比如利用自動定階的方法,得出一個模型ARIMA(1,1,0) ```r library(forecast) auto.arima(train.data,trace=TRUE) #Best model is ARIMA(1,1,0) ``` 經過比較發現還是模型ARIMA(2,2,2)較優: ```r data.autofit<-arima(train.data,order=c(1,1,0)) AIC(data.autofit) BIC(data.autofit) data.fit<-arima(train.data,order=c(2,2,2)) AIC(data.fit) BIC(data.fit) ``` | Model | AIC | BIC | | :-----------:| :-------:| :-------:| | ARIMA(1,1,0) | 930.5894 | 934.6755 | | ARIMA(2,2,2) | 919.8881 | 930.0149 | ###### 4.2 Model Validation 對擬合殘差進行白噪聲檢驗,得到p-value = 0.8221 > 0.05,而且acf在lag=1後迅速減小,可得殘差為白噪聲。 ```r forecast <-forecast(data.fit, h=4, level=c(99.5)) forecast.data <- data.frame("Date"=index(train), "Input"=forecast$x, "Fitted"=forecast$fitted, "Residuals"=forecast$residuals) acf(forecast.data$Residuals) Box.test(forecast.data$Residuals, lag=sqrt(length(forecast.data$Residuals)), type = "Ljung-Box") ``` 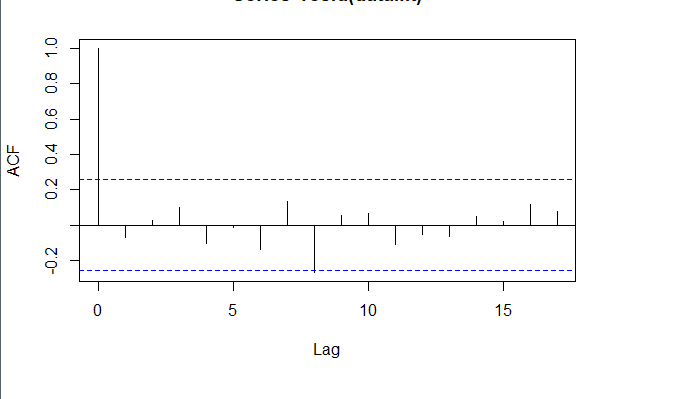 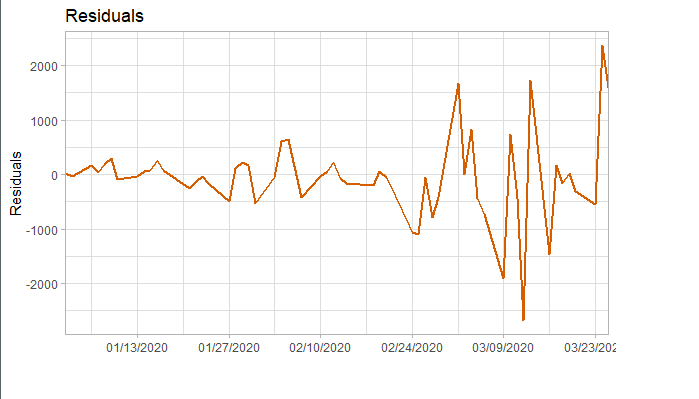 我們將訓練集資料和擬合數據同時畫在圖上,可以看到兩者的差別是在可接受範圍的。 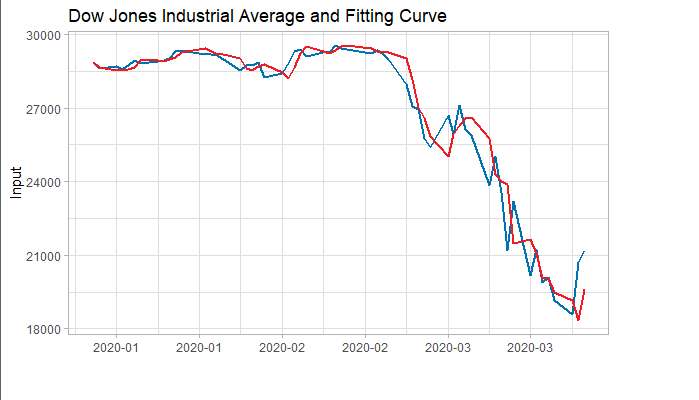 ###### 4.3 Forecast and Test Data 將預測結果與測試集對比,兩者的最大相對誤差為 0.056,可見模型是表達充分的,預測結果良好。 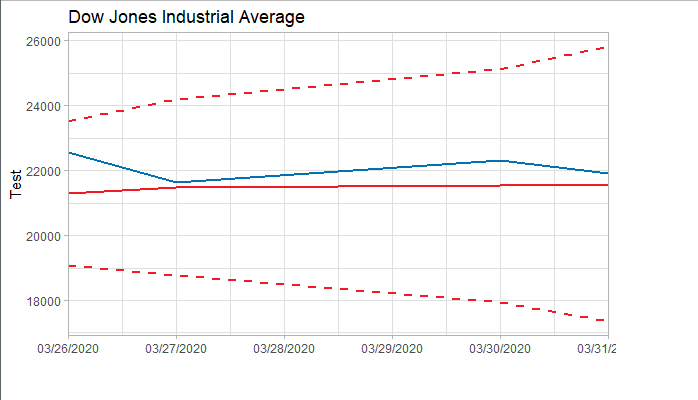 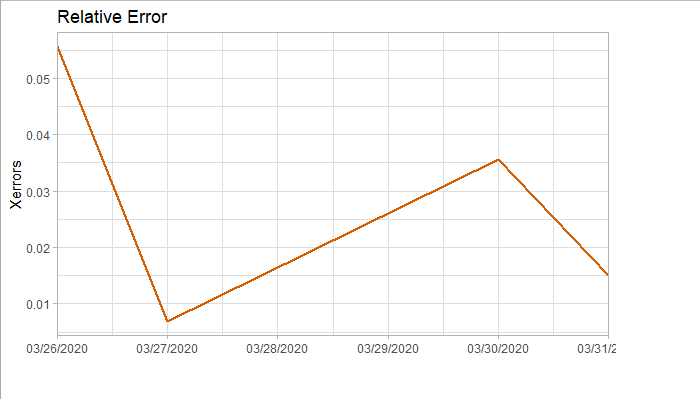 #### 5. Forecast
上述已經找到合適的預測模型了, 於是就可以用這個模型ARIMA(2,2,2)來預測未來5天的道指走勢了。預測未來道指將在22000波動,均值微跌(呈下跌趨勢),波動範圍為16000-26000左右。簡單說,這個模型的預測是前景不容樂觀。 ```r data.forecast<-arima(stock,order=c(2,2,2)) newforecast<-forecast(data.forecast, h=5, level=c(99.5)) ``` 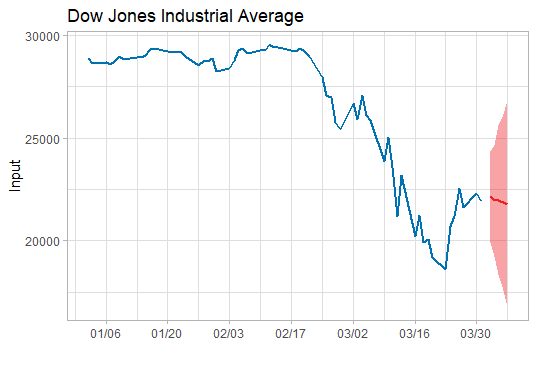 ,將前面95%的資料用作本次預測的訓練集,後面5%的資料用作本次預測的測試集。 ```r library(quantmod) stock <- getSymbols("^DJI", from="2020-01-01", from="2020-03-31", auto.assign=FALSE) names(stock) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted") stock <- stock$Close stock <- na.omit(stock) train.id <- 1: (0.95*length(stock)) train <- stock[train.id] test <- stock[-train.id] ``` #### 2. Stationarity Test
由於ARIMA預測要求輸入資料為平穩時間序列。如果輸入資料為非平穩時間序列,則需要對資料進行平穩化處理。識別資料集是否為平穩時間序列,本例子用了兩種方法:1)簡單粗暴的觀察法;2)白噪聲檢驗。 其實對於多次熔斷向下再向下的道指來說,撇開各種觀察和檢驗的方法,我們都知道他一定是非平穩時間序列了。下面兩種方法就是打個版:當我們遇到不太明顯的時間序列時可以怎麼做? ###### 2.1 Observational Method 下圖斷崖式下降的曲線表明訓練集為非平穩時間序列。 ```r library(ggplot2) library(scales) plot<-ggplot(data=train) + geom_line(aes(x=as.Date(Index), y=Close), size=1, color="#0072B2")+ scale_x_date(labels=date_format("%m/%d/%Y"), breaks=date_breaks("2 weeks"))+ ggtitle("Dow Jones Industrial Average") + xlab("")+ theme_light() print(plot) ```  ###### 2.2 Ljung‐Box Statistics Test 利用 Ljung–Box test 得到 p-value = 2.2e-16 < 0.05, 由此拒絕時間序列為白噪聲的假設。 ```r Box.test(train, lag=1, type = "Ljung-Box") ``` #### 3. Differencing
上述我們可知本訓練集為非平穩時間序列,所以我們利用差分對它進行平穩化處理。對訓練集分別進行一階差分和二階差分後,從下圖其實並不能很容易看出一階差分以及二階差分是否為平穩序列。於是我們對其進行了ADF檢驗。從檢驗結果可知: 原序列:p-value = 0.5336 > 0.05,拒絕它是平穩序列的假設; 一階差分:p-value = 0.4495 > 0.05,拒絕它是平穩序列的假設; 二階差分:p-value = 0.01 < 0.05,接受它是平穩序列的假設。 所以我們將利用其二階差分序列進行ARIMA預測。 ```r library("tseries") train.diff1 <- diff(train, lag = 1, differences = 1) train.diff2 <- diff(train, lag = 1, differences = 2) adf.test(train) adf.test(na.exclude(train.diff1)) adf.test(na.exclude(train.diff2)) ```  #### 4. ARIMA Model
###### 4.1 Choosing the order 當我們確定用二階差分序列進行預測後,則需要對模型進行定階。如下圖所示,對於ACF,滯後1-2階在2倍標準差外,所以q=2;對於PACF,同樣也是滯後1-2階都在2倍標準差外,所以p=2,所以將會選擇模型ARIMA(2,2,2)。 ```r acf <- acf(na.omit(train.data.diff2$Close), plot=TRUE) pacf <- pacf(na.omit(train.data.diff2$Close), plot=TRUE) ```   為了保證選擇的模型是最優的,建議可以多選擇接近的模型,然後根據AIC準則或者BIC準則選取最優的模型。比如利用自動定階的方法,得出一個模型ARIMA(1,1,0) ```r library(forecast) auto.arima(train.data,trace=TRUE) #Best model is ARIMA(1,1,0) ``` 經過比較發現還是模型ARIMA(2,2,2)較優: ```r data.autofit<-arima(train.data,order=c(1,1,0)) AIC(data.autofit) BIC(data.autofit) data.fit<-arima(train.data,order=c(2,2,2)) AIC(data.fit) BIC(data.fit) ``` | Model | AIC | BIC | | :-----------:| :-------:| :-------:| | ARIMA(1,1,0) | 930.5894 | 934.6755 | | ARIMA(2,2,2) | 919.8881 | 930.0149 | ###### 4.2 Model Validation 對擬合殘差進行白噪聲檢驗,得到p-value = 0.8221 > 0.05,而且acf在lag=1後迅速減小,可得殘差為白噪聲。 ```r forecast <-forecast(data.fit, h=4, level=c(99.5)) forecast.data <- data.frame("Date"=index(train), "Input"=forecast$x, "Fitted"=forecast$fitted, "Residuals"=forecast$residuals) acf(forecast.data$Residuals) Box.test(forecast.data$Residuals, lag=sqrt(length(forecast.data$Residuals)), type = "Ljung-Box") ```   我們將訓練集資料和擬合數據同時畫在圖上,可以看到兩者的差別是在可接受範圍的。  ###### 4.3 Forecast and Test Data 將預測結果與測試集對比,兩者的最大相對誤差為 0.056,可見模型是表達充分的,預測結果良好。   #### 5. Forecast
上述已經找到合適的預測模型了, 於是就可以用這個模型ARIMA(2,2,2)來預測未來5天的道指走勢了。預測未來道指將在22000波動,均值微跌(呈下跌趨勢),波動範圍為16000-26000左右。簡單說,這個模型的預測是前景不容樂觀。 ```r data.forecast<-arima(stock,order=c(2,2,2)) newforecast<-forecast(data.forecast, h=5, level=c(99.5)) ```  