資料探勘入門系列教程(八)之使用神經網路(基於pybrain)識別數字手寫集MNIST
阿新 • • 發佈:2020-04-05
[TOC]
## 資料探勘入門系列教程(八)之使用神經網路(基於pybrain)識別數字手寫集MNIST
在本章節中,並不會對神經網路進行介紹,因此如果不瞭解神經網路的話,強烈推薦先去看《西瓜書》,或者看一下我的上一篇部落格:[資料探勘入門系列教程(七點五)之神經網路介紹](https://www.cnblogs.com/xiaohuiduan/p/12623925.html)
本來是打算按照《Python資料探勘入門與實踐》裡面的步驟使用神經網路來識別驗證碼,但是呢,驗證碼要自己生成,然後我又想了一下,不是有大名鼎鼎的MNIST資料集嗎,為什麼不使用它呢,他不香嗎?
MNIST(Mixed National Institute of Standards and Technology database)相信大家基本上都瞭解過他,大部分的機器學習入門專案就是它。它是一個非常龐大的手寫**數字**資料集([官網](http://yann.lecun.com/exdb/mnist/))。裡面包含了0~9的手寫的數字。部分資料如下:

資料集分為兩個部分,訓練集和測試集。然後在不同的集合中分為兩個檔案,資料Images檔案和Labels檔案。在資料集中一個有60,000個訓練資料和10,000個測試資料。圖片的大小是28*28。

### 下載資料集
萬物始於資料集,儘管官網提供了資料集供我們下載,但是在**sklearn**中提供了更方便方法讓我們下載資料集。程式碼如下:
```python
import numpy as np
from sklearn.datasets import fetch_openml
# X為image資料,y為標籤
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
```
其中X,y中間既包含了訓練集又包含了測試集。也就是說X或者y中有70,000條資料。 那麼資料是什麼呢?
在X中,每一條資料是一個長為$28 \times 28=784$的陣列,陣列的資料是圖片的畫素值。每一條y資料就是一個標籤,代表這張圖片表示哪一個數字(從0到9)。
然後我們將資料進行二值化,畫素值大於0的置為1,並將資料儲存到資料夾中:
```python
X[X > 0 ] = 1
np.save("./Data/dataset",X)
np.save("./Data/class",y)
```
然後在Data資料夾中就出現了以下兩個檔案:

我們取出dataset中間的一條資料,然後轉成28*28的格式,如下所示:

資料集既可以使用上面的方法得到,也可以從我的[Github](https://github.com/xiaohuiduan/data_mining/tree/master/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/Data)上面進行下載(其中dataset資料集因為GitHub檔案大小的限制所以進行了壓縮,需要解壓才能夠使用)。
### 載入資料集
前面的步驟我們下載好了資料集,現在我們就可以來載入資料了。
````python
import numpy as np
X = np.load("./Data/dataset.npy")
y = np.load("./Data/class.npy")
````
取出X中的一條資料如下所示:

取出y中的一條資料,如下所示:

一切都很完美,但是這裡有一個問題,在神經網路中,輸出層實際上是這樣的:
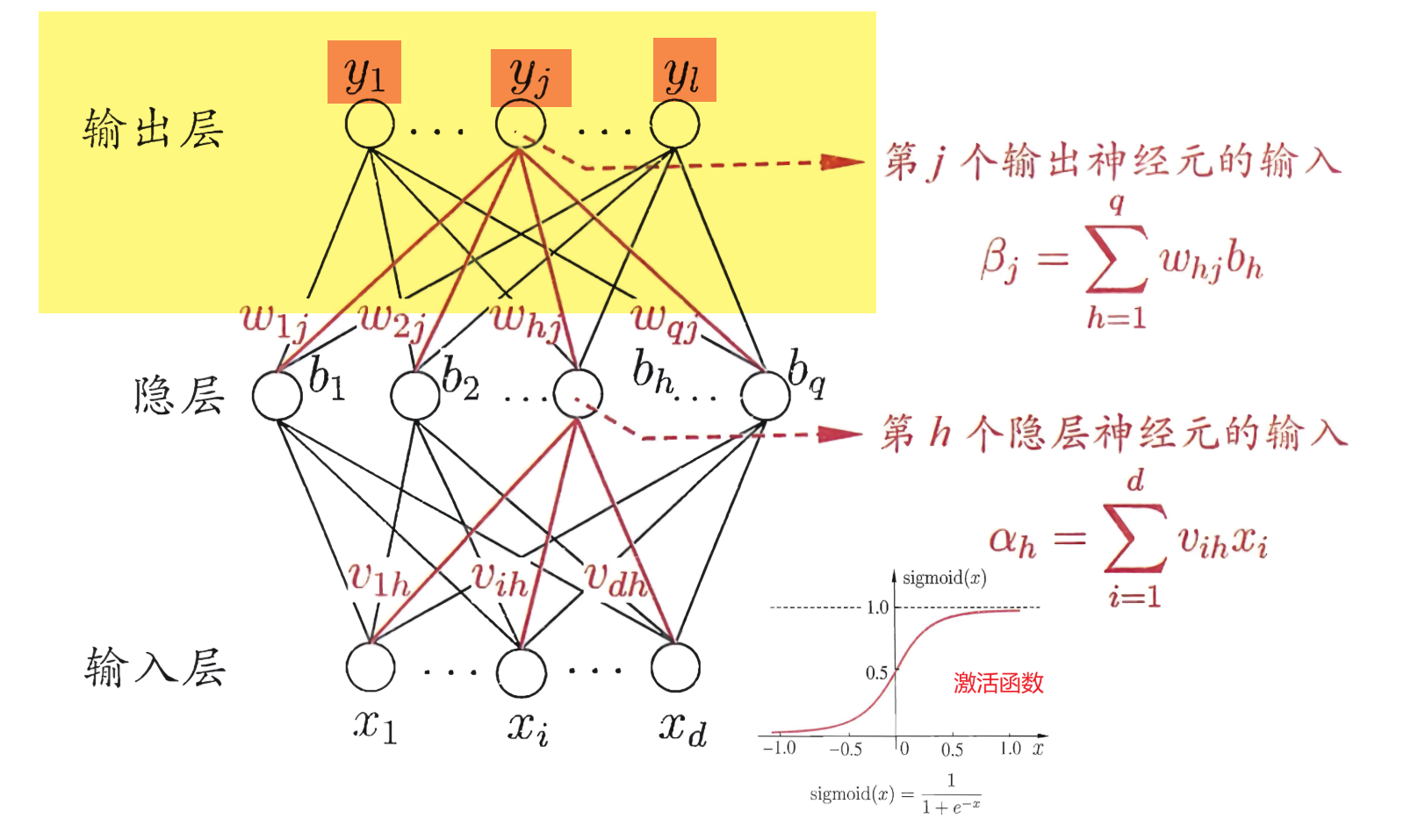
它並不是直接輸出某一個結果,而是輸出$y_1,…,y_j,…,y_l$結果(在MNIST中$l=10$,因為只有10種數字)。以上面的5為例子,輸出層並不是單純的輸出只輸出一個數字,而是要輸出10個值。那麼如何將輸出5變成輸出10個數字呢?這裡我們使用”one hot Encoding“。
One-Hot編碼,又稱為一位有效編碼,主要是採用$N$位狀態暫存器來對$N$個狀態進行編碼,每個狀態都由他獨立的暫存器位,並且在任意時候只有一位有效。
以下面的資料為例,每一行代表一條資料,每一列代表一個屬性。其中第2個屬性只需要3個狀態碼,因為他只有0,1,2三種屬性。這樣我們就可以使用100代表0,010代表1,001代表2。
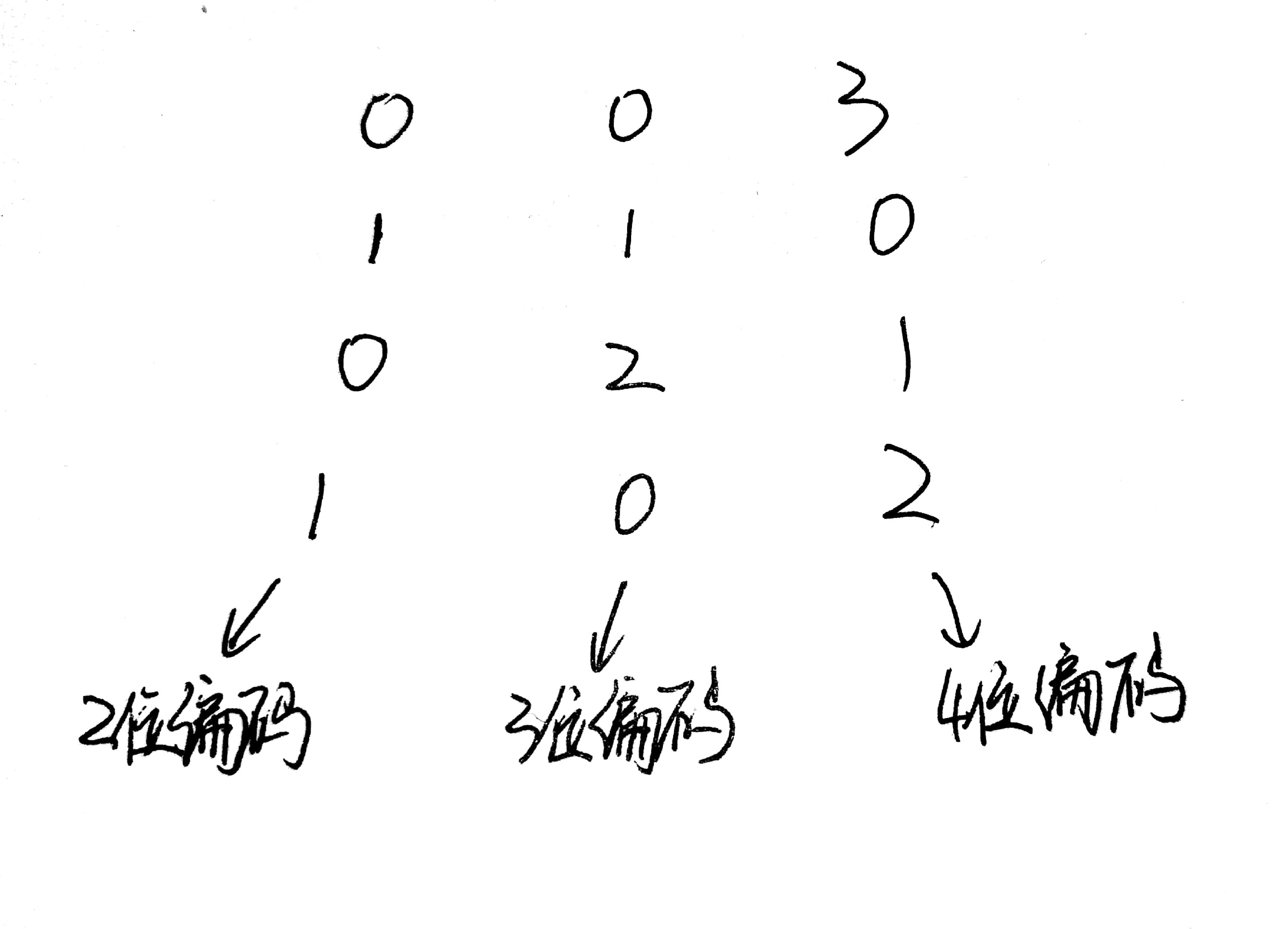
那麼這個資料編碼後的資料長什麼樣呢?如下圖:

現在我們就可以將前面載入的資料集標籤$y$進行“one hot Encoding”。
程式碼如下:
```python
from sklearn.preprocessing import OneHotEncoder
# False代表不生成稀疏矩陣
onehot = OneHotEncoder(sparse = False)
# 首先將y轉成行長為7000,列長為1的矩陣,然後再進行轉化。
y = onehot.fit_transform(y.reshape(y.shape[0],1))
```
接著就是切割資料集了。將資料集切割成訓練集和測試集。
```python
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(X,y,random_state=14)
```
在神經網路中,我們使用[pybrain](http://pybrain.org/)框架去構建一個神經網路。但是呢,對於pybrain庫,他很與眾不同,他要使用自己的資料集格式,因此,我們需要將資料轉成它規定的格式。
```python
from pybrain.datasets import SupervisedDataSet
train_data = SupervisedDataSet(x_train.shape[1],y.shape[1])
test_data = SupervisedDataSet(x_test.shape[1],y.shape[1])
for i in range(x_train.shape[0]):
train_data.addSample(x_train[i],y_train[i])
for i in range(x_test.shape[0]):
test_data.addSample(x_test[i],y_test[i])
```
終於,資料集的載入就到這裡結束了。接下來我們就可以開始構建一個神經網路了。
### 構建神經網路
首先我們來建立一個神經網路,網路中只含有輸入層,輸出層和一層隱層。
```python
from pybrain.tools.shortcuts import buildNetwork
# X.shape[1]代表屬性的個數,100代表隱層中神經元的個數,y.shape[1]代表輸出
net = buildNetwork(X.shape[1],100, y.shape[1], bias=True)
```
這裡說有以下“bias”的作用。bias代表的是偏置神經元,bias = True代表偏置神經元啟用,也就是在每一層都使用這個這個神經元。偏置神經元如下圖,實際上也就是閾值,只不過換一種說法而已。
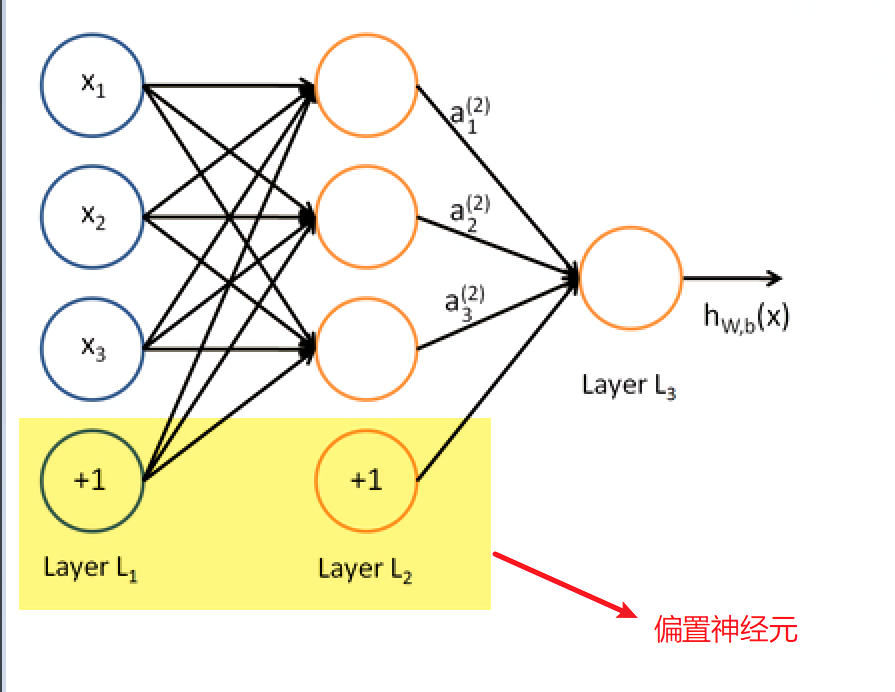
現在我們已經構建好了一個比較簡單的神經網路,接下來我們就是使用BP演算法去得到合適的權重值了。
### 反向傳播(BP)演算法
具體的演算法步驟在上一篇[部落格](https://www.cnblogs.com/xiaohuiduan/p/12623925.html)已經介紹過了,很幸運的是在pybrain中間提供了BP演算法的庫供我們使用。這裡就直接上程式碼吧。關於BackpropTrainer更加細節的使用可以看[官網](http://pybrain.org/docs/api/supervised/trainers.html)
```python
from pybrain.supervised.trainers import BackpropTrainer
trainer = BackpropTrainer(net, train_data, learningrate=0.01,weightdecay=0.01)
```
這裡面有幾個引數稍微的說明下:
- net:神經網路
- train_data:訓練的資料集
- learningrate:學習率,也就是下面的$\eta$,同樣它可以使用*lrdecay*這個引數去控制衰減率,具體的就去看[官網文件](http://pybrain.org/docs/api/supervised/trainers.html)吧。
$$
\begin{equation}\begin{array}{l}
\Delta w_{h j}=\eta g_{j} b_{h} \\
\Delta \theta_{j}=-\eta g_{j} \\
\Delta v_{i h}=\eta e_{h} x_{i} \\
\Delta \gamma_{h}=-\eta e_{h} \\
\end{array}\end{equation}
$$
- weightdecay:權重衰減,權重衰減也就是下面的$\lambda$
$$
\begin{equation}
E=\lambda \frac{1}{m} \sum_{k=1}^{m} E_{k}+(1-\lambda) \sum_{i} w_{i}^{2} \\
\lambda \in(0,1)
\end{equation}
$$
然後我們就可以開始訓練了。
```python
trainer.trainEpochs(epochs=100)
```
`epochs`也就是訓練集被訓練遍歷的次數。
接下載便是等待的時間了。等待訓練集訓練成完成。訓練的時間跟訓練集的大小,隱層神經元的個數,電腦的效能,步數等等有關。
切記切記,這一次的程式就不要在阿里雲的學生機上面跑了,還是用自己的機器跑吧。儘管聯想小新pro13 i5版本效能還可以,但是還是跑了一個世紀這麼久,哎(耽誤了我打遊戲的時間)。
### 進行預測
通過前面的步驟以及等待一段時間後,我們就完成了模型的訓練。然後我們就可以使用測試集進行預測。
````python
predictions = trainer.testOnClassData(dataset=test_data)
````
`predictions`的部分資料,代表著測試集預測的結果:

然後我們就可以開始驗證準確度了,這裡繼續使用F1評估。這個已經在前面介紹過了,就不再介紹了。
### F1驗證
這裡有個地方需要注意,因為之前的`y_test`資料我們使用`one-hot encoding`進行了編碼,因此我們需要先將`one-hot`編碼轉成正常的形式。
```python
# 取每一行最大值的索引。
y_test_arry = y_test.argmax(axis =1)
```
具體效果如下:

然後使用`F1`值進行驗證。
```python
from sklearn.metrics import f1_score
print("F-score: {0:.2f}".format(f1_score(predictions,y_test_arry,average='micro')))
```
然後結果如下:

結果只能說還行吧,不是特別的差,但是也不是特別的好。
### 總結
專案地址:[Github](https://github.com/xiaohuiduan/data_mining/tree/master/%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C)。儘管上面的準確度不咋地,只有$86\%$,但是也還行吧,畢竟也是使用了一層隱層,然後隱層也只有100個神經元。
如果電腦的效能不夠的話,可是適當的減少步數和訓練集的大小,以及隱層神經元的個數。
#### 參考
- [wikipedia](https://en.wikipedia.org/wiki/MNIST_database)
- 《Python資料探勘入門與實踐》
- [pybrain](http://pybra
