目錄

• SVM介紹
• 線性分類
• 間隔
• 最大間隔分類器
• 拉格朗日乘子法（Lagrange multipliers）
  • 拉格朗日乘子法推導
  • KKT條件（Karush-Kuhn-Tucker Conditions）
  • 拉格朗日乘子法對偶問題
  • Slater 條件
• 最大間隔分類器與拉格朗日乘子法
• 核技巧
  • 核函式
• 軟間隔
  • 軟間隔支援向量機推導
• SMO演算法
  • SMO變數的選擇方法
• 總結
  • 參考

還是老規矩，這一篇部落格是對SVM進行介紹，下一篇部落格就是使用SVM進行具體的使用。

SVM介紹

首先介紹SVM是什麼，SVM（support vector machine）名為支援向量機，又名支援向量網路，是一個非常經典且高效的分類模型，是一種監督式的學習方法。

從名字上面來理解，SVM分為兩個部分，"支援向量（support vector）"以及“機（machine）”。“machine”很簡單的理解，就是演算法的意思，那麼“support vector”是什麼呢？ 這個現在不進行介紹，待我慢慢的引入。

線性分類

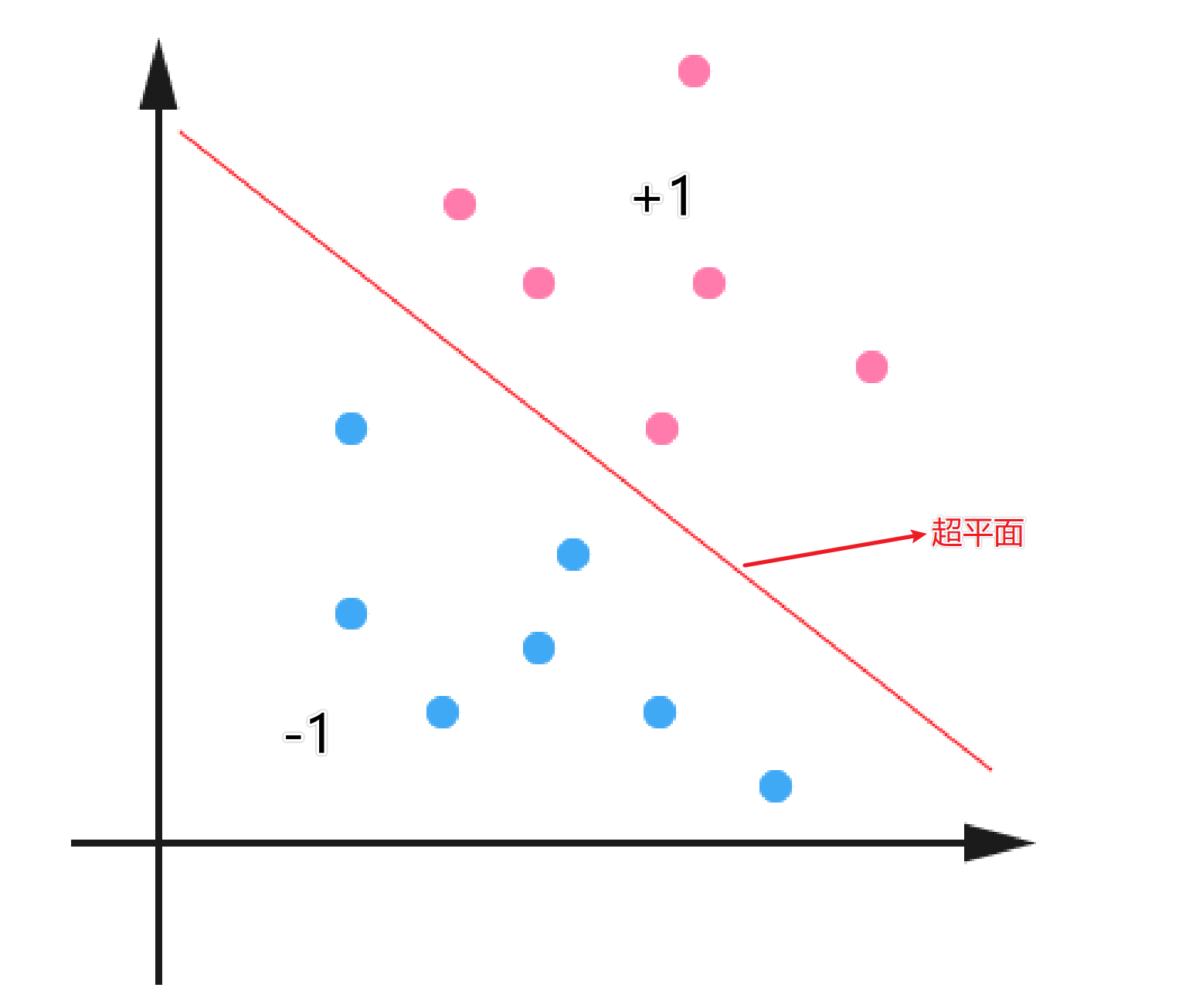
在介紹SVM之前，我們得先對線性分類器進行介紹。下面是一個二維平面的的分類問題，紅色代表類別為+1，藍色的代表類別是-1。中間的線就代表分割這兩類問題的超平面。對於分類問題來說，紅色和藍色的點都是資料集中已知的，而我們的目的就是找到一個最適合的超平面，將資料進行分類。

對於線性二分類模型，給定一組資料\(\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\}\)， 其中\(\boldsymbol{x}_{i} \in \mathbb{R}^{d}, y \in\{-1,1\}\)，二分類任務的目標是希望從資料中學得一個假設函式\(h: \mathbb{R} \rightarrow\{-1,1\}\)，使得\(h(x_i) = y_i\)

\[\begin{equation} h\left(\boldsymbol{x}_{i}\right)=\left\{\begin{array}{ll} 1 & 若 y_{i}=1 \\ -1 & 若 y_{i}=-1\\\tag{1} \end{array}\right. \end{equation} \]

那麼問題來了，我們如何去尋找一個能夠將\(y_i = \pm1\)劃分開的超平面？首先我們可以設超平面的函式是：

\[\begin{equation}f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\end{equation} \tag{2} \]

這裡有一個值得注意的點，下面的這個公式會在後面的推導中經常用到。

\[y_i^2 = 1 \tag{3} \]

儘管有很多的問題都是線性不可分的，但是呢，目前我們只討論線性可分問題，到後面我們再討論如何將非線性問題轉成線性問題。因此，暫時我們不需要去糾結如果是非線性問題怎麼辦。

我們可以直觀的從圖中進行感受，這樣的超平面是有多個的，那麼如何尋找一個最合適的超平面呢（也就是尋找最合適的\(w^{\mathrm{T}}\) 和\(b\)）？接下來引出間隔的概念來尋找最合適的超平面。

間隔

如下圖所示，超平面\(\begin{equation}f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\end{equation}\)，則\(x\)為\(x_0\)到超平面的投影，\(x_0\)對應的類別是\(y_0\)，\(w\)為超平面的法向量，\(\gamma\)為\(x_0\)到超平面的距離（帶正負號）。

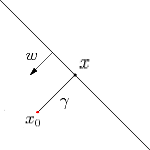
因此

\[\begin{aligned} & \gamma = \frac{f(x_0)}{||w||} \\ & 因此距離（不帶正負號）的為: \\ & \tilde{\gamma} = y_0\gamma \end{aligned} \]

這樣我們就推出了間隔的表示式\(\tilde{\gamma} = y_0\gamma\)。對於給定的資料集，我們當然是希望資料集中的資料離超平面越遠越好，因為這樣所能夠容忍的誤差也就越大。那麼這個遠如何來確定呢？接下來讓我們討論什麼是最大間隔分類器。

最大間隔分類器

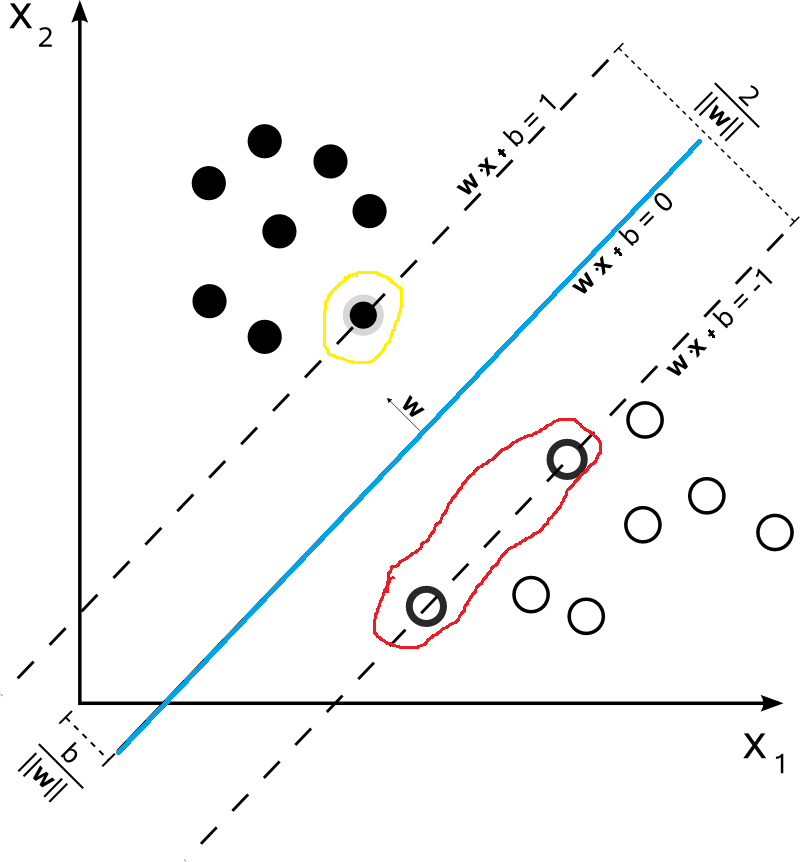
如果我們給定如下的資料集，那麼對於下面的資料集，哪一些最不可能分類成功呢？毋庸置疑的，就是最靠近\(\begin{equation}f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\end{equation}\)超平面的資料點(比如下圖中被紅色和黃色圈出來的點)。而被圈出來的點也就是被稱之為“支援向量”。因為在模型中我們考慮他們就可以了。

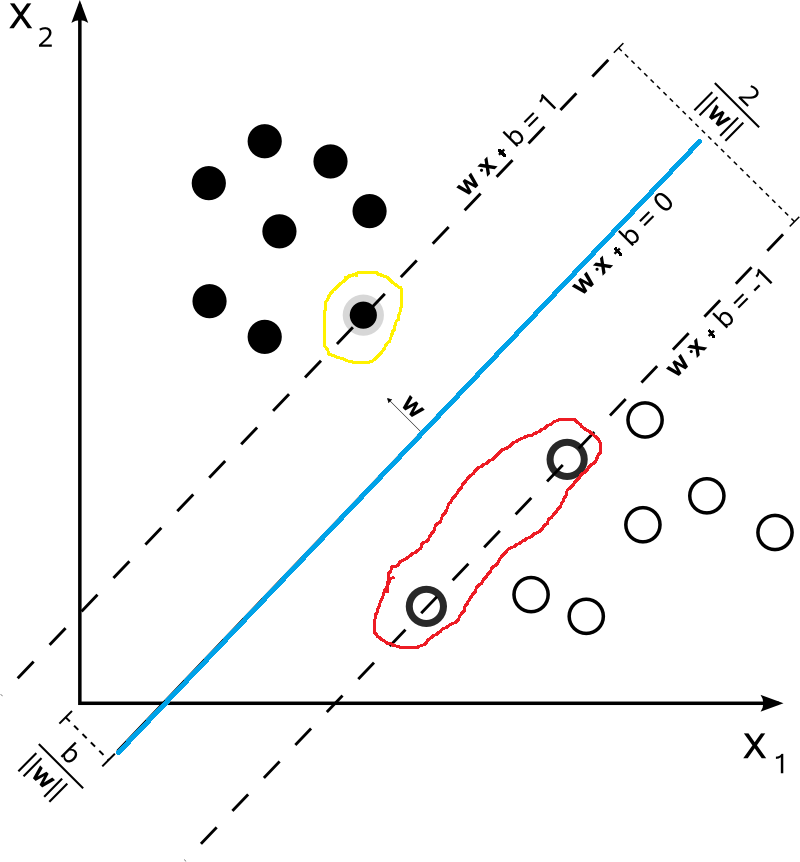
首先我們假設支援向量分佈在\(\omega^Tx+b=\pm 1\)超平面上，這裡取值為1只是為了方便，該值並不影響後面的優化結果。很顯然，支援向量到超平面\(\omega^Tx+b=\pm 1\)的距離為\(\frac{1}{\|\omega\|}\)。兩側的距離加起來就是\(\frac{2}{\|\omega\|}\)。在前面我們說過，我們希望距離越大越好，也就是說\(\frac{2}{\|\omega\|}\)越大越好，同時對於資料集中資料的分佈滿足\(y(\omega^T+b)x \geqslant 1\)。因此，我們得到了如下的優化問題：

\[\left \{ \begin{matrix} \begin{align*} & \max \quad \frac{2}{\Vert \omega \Vert} \\ & s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \end{align*} \end{matrix} \right. \tag{4} \]

為了方便後續的推導，該優化問題等價於：

\[\left \{ \begin{matrix} \begin{align*} & \min \quad \frac{1}{2}\| \omega \|^2 \\ & s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \end{align*} \end{matrix} \right. \tag{5} \]

拉格朗日乘子法（Lagrange multipliers）

拉格朗日乘子法是一種尋找多元函式在一組約束下的極值的方法。通過引拉格朗日乘子，可將有 \(d\)個變數與\(k\)個約束條件的最優化問題轉化為具有\(d+k\)個變數的無約束優化問題求解。下面讓我們來進行推導。

拉格朗日乘子法推導

如下圖所示\(z=f(x,y)\)，\(g(x,y)=0\)，如果我們需要求\(z\)在\(g(x,y)\)條件下的極值。從幾何角度來說，我們可以畫出\(z = C_i\)的等高線，等高線與\(g(x,y)\)相切的點\((x_0,y_0)\)即為極值點。如下圖所示：

因為在點\((x_0,y_0)\)取得極值，那麼，\(\nabla{f(x_0, y_0)} // \nabla{g(x_0, y_0)}\)，也就是說此時梯度平行。也就是說\(({f_x}'(x_0,y_0),{f_y}'(x_0,y_0)) // ({g_x}'(x_0,y_0),{g_y}'(x_0,y_0))\)（這個是可以證明的，但是在這裡就不證明了）因此有：

\[\frac{{f_x}'(x_0,y_0)}{{g_x}'(x_0,y_0)}=\frac{{f_y}'(x_0,y_0)}{{g_y}'(x_0,y_0)}=-\lambda_0 （\lambda_0可以為0） \]

即：

\[\left\{\begin{matrix} {f_x}'(x_0,y_0)+\lambda_0{g_x}'(x_0,y_0)=0\\ \\ {f_y}'(x_0,y_0)+\lambda_0{g_y}'(x_0,y_0)=0\\ \\ g(x,y)=0 \end{matrix}\right. \tag{6} \]

如果此時我們有一個輔助函式\(L(x,y, \lambda)=f(x,y)+\lambda g(x,y)\)，對其求偏導然後求極值點可得：

\[\left\{\begin{matrix} \frac{\partial L(x,y, \lambda)}{\partial x}={f_x}'(x,y)+\lambda{g_x}'(x,y)=0\\ \\ \frac{\partial L(x,y, \lambda)}{\partial y}={f_y}'(x,y)+\lambda{g_y}'(x,y)=0\\ \\ \frac{\partial L(x,y, \lambda)}{\partial \lambda}=g(x,y)=0 \end{matrix}\right. \tag{7} \]

顯而易見公式\((6)\)和公式\((7)\)相等。因此我們對\(z = f(x,y)\)在條件\(f(x,y) = 0\)的條件下求極值\((x_0,y_0)\)的問題變成了求拉格朗日函式\(L(x,y, \lambda)=f(x,y)+\lambda g(x,y)\)偏導數為0的解。

KKT條件（Karush-Kuhn-Tucker Conditions）

上面我們討論的是在等式約束條件下求函式極值的問題（也就是\(g(x,y)=0\)）but，如果如果是不等式條件下，我們應該如何來使用拉格朗日函式來求解呢？下面引出KKT條件。

什麼是KKT條件呢？它是在滿足一些有規則的條件下，一個非線性規劃問題能有最優化解法的一個必要條件。也就是說優化問題在最優值處必須滿足KKT條件。

例如我們有以下優化問題：

\[\begin{equation}\begin{aligned} \min _{x} & f(x) \\ \text { s.t. } & h_{i}(x)=0 \quad(i=1, \ldots, m) \\ & g_{j}(x) \leqslant 0 \quad(j=1, \ldots, n) \end{aligned}\end{equation} \]

其拉格朗日函式為：

\[\begin{equation}L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x})\end{equation} \tag{8} \]

則其KKT條件為：

\[\begin{equation}\left\{\begin{array}{l} g_{j}(\boldsymbol{x}) \leqslant 0 \\ \mu_{j} \geqslant 0 \\ \mu_{j} g_{j}(\boldsymbol{x})=0 \\ h(x) =0 \end{array}\right.\end{equation} \]

接下來讓我們來解釋一下為什麼是這樣的。（不一定是數學證明）。

下面我們只討論\(f(x)\)在不等式\(g_i(x)<0\)條件下取\(min\)情況。這裡可能有人會說，如果我要求\(max\)怎麼辦？很簡單那，將\(f(x)\)取反即可，就變成了求\(min\)的情況。同樣對於\(g_i(x) > 0\)的情況，我們取反就變成了\(g^{'}(x) = -g_i(x) \lt 0\)。

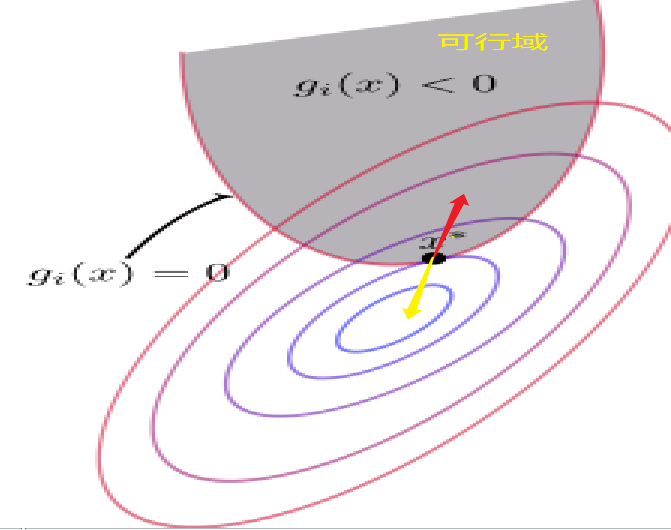
對於上述討論，有兩種情況如下圖（圖中\(x^*\)代表極小值點）：

• 情況一：極小值點\(x^*\)在\(g_i(x)<0\)的區域內
• 情況二：極小值點\(x^*\)在\(g_i(x)=0\)上

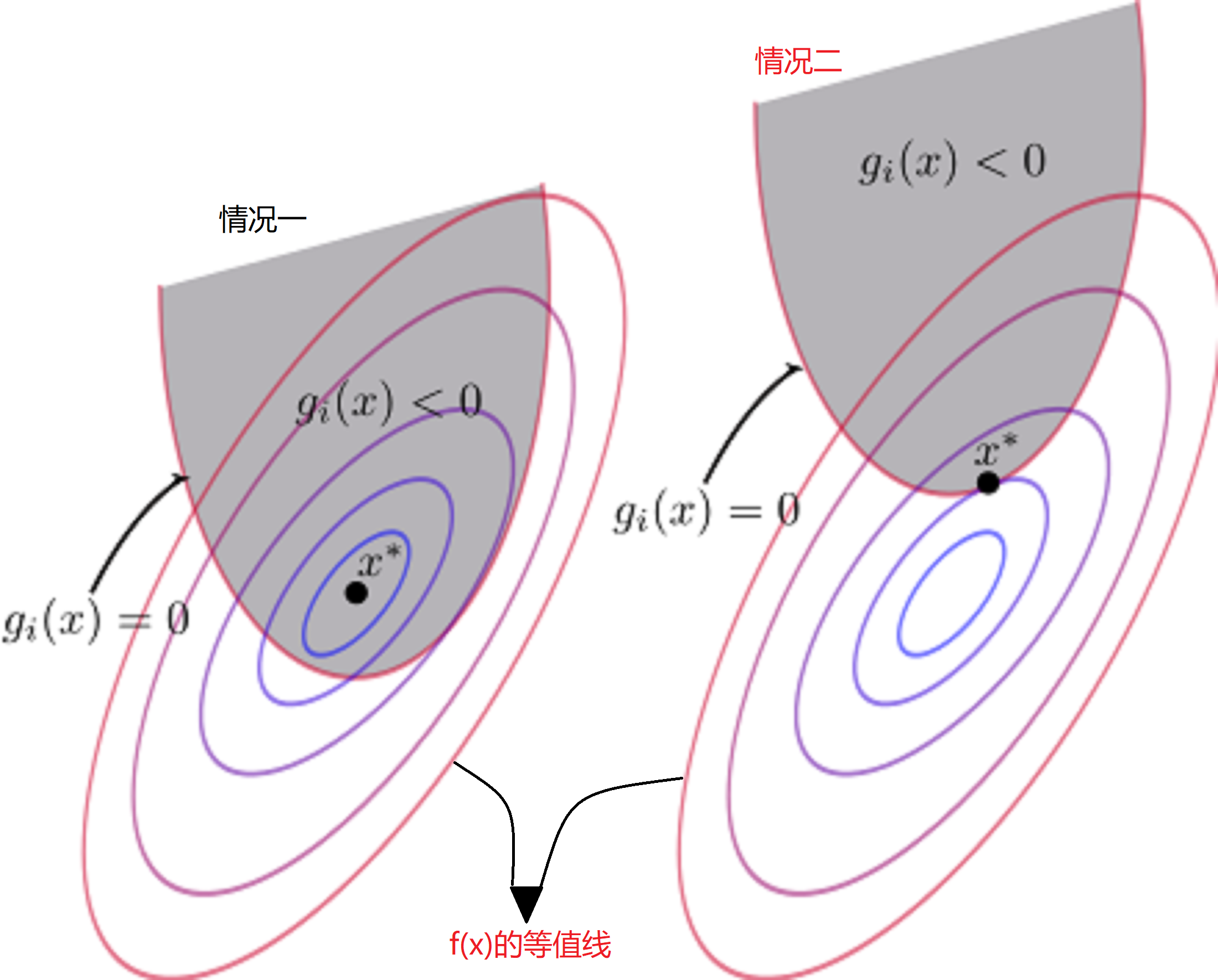
首先我們先討論情況二，對於情況二很好理解，此時的“不等式約束”變成了“等式約束”。那麼其在極值點滿足以下條件：

\[h(x)=0\\ g(x)=0\\ \mu \geq 0 \tag{9} \]

\(h(x)=0，g(x)=0\)我們很好理解，但是為什麼我們對\(\mu\)還要進行限制呢？然後為什麼限制還為\(\mu \geq 0\)呢？首先我們來考慮一下\(f(x)\)和\(g(x)\)在\(x^*\)點的梯度方向（首先\(f(x)\)和\(g(x)\)在\(x^*\)點的梯度方向肯定是平行的【梯度的方向代表函式值增加最快的方向】）。

• 對於\(f(x)\)來說，等值線大小由中心到周圍逐漸增大，因此它的梯度方向指向可行域。為圖中紅色的箭頭號。
• 對於\(g(x)\)來說，梯度方向肯定是指向大於0的一側，那麼就是要背離可行域。為圖中黃色的箭頭號。

在前面拉格朗日乘子法中我們有以下推導：

\[\frac{{f_x}'(x_0,y_0)}{{g_x}'(x_0,y_0)}=\frac{{f_y}'(x_0,y_0)}{{g_y}'(x_0,y_0)}=-\lambda_0 （\lambda_0可以為0） \]

又因為\(g(x)\)和\(f(x)\)梯度方向相反，因此\(\lambda_0 \geq0\)。 因此對於\(公式9\)有\(\mu \geq 0\)。

接下來讓我們來討論情況一。情況一是極小值$x^* \(在\)g(x)$的可行域中，因此，我們可以將其看成沒有不等式約束條件。那麼其在極值點滿足以下條件：

\[h(x)=0\\ g(x) \leq 0\\ \mu =0 \]

對比兩種情況：

• 情況一：\(\mu = 0，g(x) \leq 0\)
• 情況二：\(\mu \geq 0，g(x)=0\)

綜合情況一和情況二，可得到KKT條件為：

\[\begin{equation}\left\{\begin{array}{l} g_{j}(\boldsymbol{x}) \leqslant 0 \quad(主問題可行)\\ \mu_{j} \geqslant 0 \quad(對偶問題可行)\\ \mu_{j} g_{j}(\boldsymbol{x})=0 \quad(互補鬆弛)\\ h(x) =0 \end{array}\right.\end{equation} \]

拉格朗日乘子法對偶問題

對於如下優化問題：

\[\begin{equation}\begin{aligned} \min _{x} & f(x) \\ \text { s.t. } & h_{i}(x)=0 \quad(i=1, \ldots, m) \\ & g_{j}(x) \leqslant 0 \quad(j=1, \ldots, n) \end{aligned}\end{equation} \tag{10} \]

其拉格朗日函式為：

\[\begin{equation} L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x}) \\ s.t. \mu_j \ge0 \end{equation} \]

對於上述的優化問題（\(公式10\)）我們可以等價於（下面的稱之為主問題）：

\[\begin{equation}\begin{aligned} \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} & \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ \text { s.t. } & \mu_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \]

證明如下：

\[\begin{equation}\begin{aligned} & \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}}\mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ =& \min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\max _{\boldsymbol{\lambda}, \boldsymbol{\mu}}\left(\sum_{i=1}^{m} \mu_{i} g_{i}(\boldsymbol{u})+\sum_{j=1}^{n} \lambda_{j} h_{j}(\boldsymbol{u})\right)\right) \\ =& \min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\left\{\begin{array}{l} 0 \text{ 若x滿足約束}\\ \infty \text{否則} \end{array}\right)\right.\\ =& \min _{\boldsymbol{u}} f(\boldsymbol{u}) \end{aligned}\end{equation} \]

其中, 當\(g_i(x)\)不滿足約束時, 即\(g_i(x)\gt0\), 我們可以令\(\mu=\infty\), 使得\(\mu_ig_i(x) = \infty\); 當\(h_j(x)\)不滿足約束時, 即 \(h_j(x)\ne0\), 我們可以取\(\lambda_j = \infty\), 使得\(\lambda_jh_j(x) = \infty\)。當\(x\)滿足約束時, 由於 \(\mu_i\ge0\)，\(g_i(x)\le0\), 則 \(\mu_ig_j(x)\le0\)，因此我們可以取最大值0。 實際上也就是說如果\(公式10\)存在最優解，則最優解必須滿足KKT條件。

對於\(公式10\)其對偶問題為：

\[\begin{equation}\begin{aligned} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x}& \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ \text { s.t. } & \mu_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \]

對偶問題是主問題的下界（他們兩個具有弱對偶性）：

\[p^* = \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \ge \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = g^* \]

你可以記憶成“廋死的駱駝比馬大”，還看到一個記憶方法為“寧為鳳尾不為雞頭”。hhh

證明如下：

\[\max _{x} \min _{y} f(x, y) \leq \min _{y} \max _{x} f(x, y)\\ \text{let } g(x)=\min _{y} f(x, y)\\ \text{then }g(x) \leq f(x, y), \forall y\\ \therefore \max _{x} g(x) \leq \max _{x} f(x, y), \forall y\\ \therefore \max _{x} g(x) \leq \min _{y} \max _{x} f(x, y) \]

Slater 條件

前面我們討論了弱對偶性，這裡我們將進行討論Slater條件，但是為什麼我們要討論Slater條件呢？原因很簡單，我們想讓上面的弱對偶問題轉成強對偶問題。

Slater定理是說，當Slater條件成立且原問題是凸優化問題時，則強對偶性成立。這裡有幾個名詞值得注意：

• 凸優化問題

  如果一個優化問題滿足如下格式，我們就稱該問題為一個凸優化問題：

  \[\begin{array}{} \text{min}&f(x)\\ \text{s.t}&g_i(x)\le0,&i=1,...,m \\ \text{ }&h_i(x)=0,&i=1,...,p \end{array} \]

  其中\(f(x)\)是凸函式，不等式約束\(g(x)\)也是凸函式，等式約束\(h(x)\)是仿射函式。

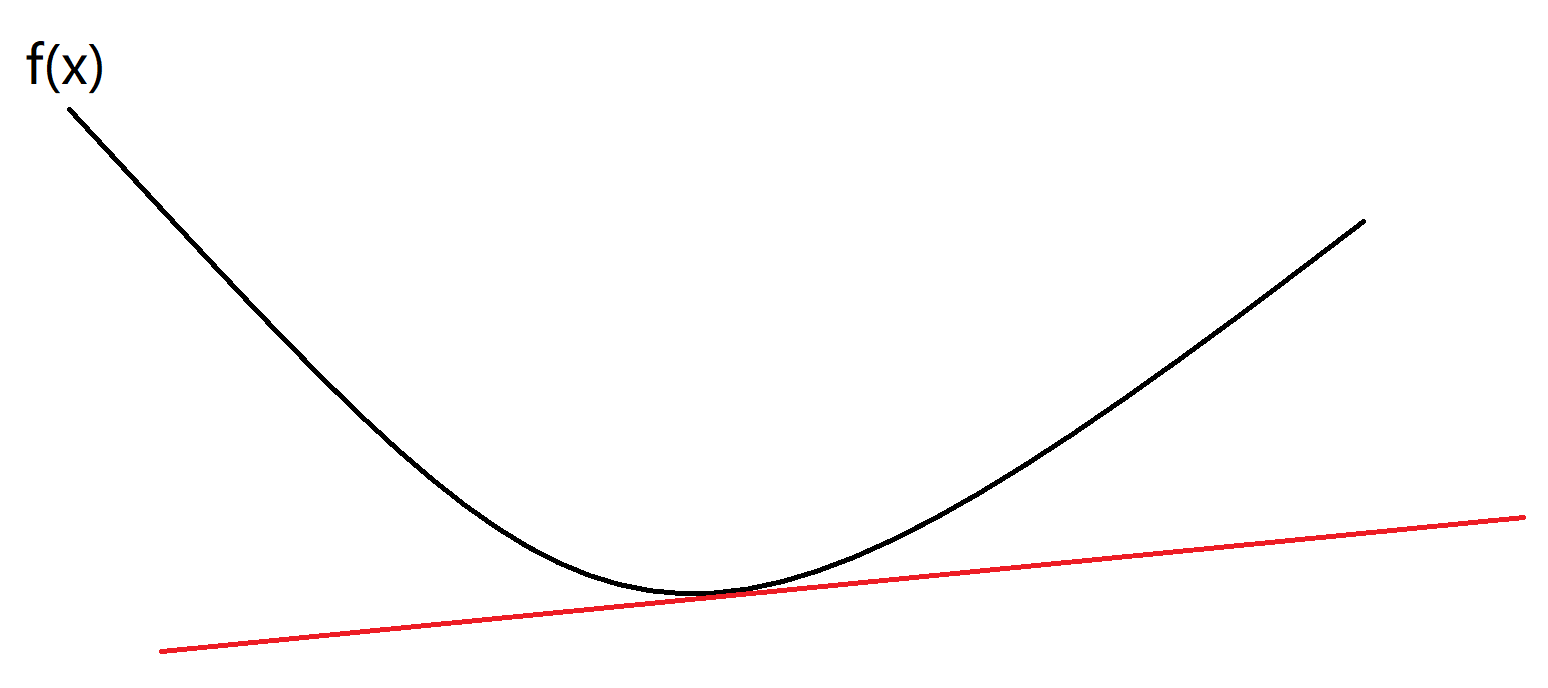
  1. 凸函式是具有如下特性的一個定義在某個向量空間的凸子集\(C\)（區間）上的實值函式\(f\)：對其定義域上任意兩點\(x_1,x_2\)總有\(f\left(\frac{x_{1}+x_{2}}{2}\right) \leq \frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2}\)。

     

  2. 仿射函式

     仿射函式，即最高次數為1的多項式函式。

• 強對偶性

  弱對偶性是\(p* = \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \ge \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = g*\)，也就是\(p^* \ge g^*\)，則強對偶性是\(p^* = g^*\)。

說了這麼多，那什麼是Slater條件呢？

1. 原問題是凸優化問題
2. 存在\(x\)使得\(g(x) \le0\)嚴格成立。（換句話說，就是存在\(x\)使得\(g(x) \lt0\)成立）

值得注意的是線性支援向量機滿足Slater條件（因為\(\frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}\)和\(1-y_{i}(w^Tx_i+b)\)均為凸函式），也就是它滿足強對偶性。

最大間隔分類器與拉格朗日乘子法

前面說了這麼多，實際上也就是為這個地方做鋪墊。我們可以將最大間隔分類問題轉化成在KKT條件下的拉格朗日函式的極值問題，然後又因為其滿足Slater條件，我們可以轉化成強對偶問題。

在最大間隔分類中，我們得到如下結論：

\[\left \{ \begin{matrix} \begin{align*} & \min \quad \frac{1}{2}\| \omega \|^2 \\ & s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \end{align*} \end{matrix} \right. \tag{11} \]

其拉格朗日函式為：

\[\begin{equation} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}):=\frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right) \\ s.t. \alpha_i \ge0,\quad i=1,2,...,m \end{equation} \]

其對偶問題（滿足強對偶性）為：

\[\begin{equation}\begin{aligned} &\max _{\alpha} \min _{\boldsymbol{w}, b}\left(\frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right)\right)\\ &\text { s.t. } \quad \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation}\tag{12} \]

然後我們來求：

\[\begin{equation}\begin{aligned} &\min _{\boldsymbol{w}, b}\left( \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b\right)\right)\right)\\ &\text { s.t. } \quad \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \]

上式對於\((\omega,b)\)屬於無約束優化問題，令偏導為零可得：

\[\begin{equation} \frac{\partial \mathcal{L}}{\partial \boldsymbol{w}}=\mathbf{0} \Rightarrow \boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\ \frac{\partial \mathcal{L}}{\partial b}=0 \Rightarrow \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \end{equation} \tag{13} \]

代入\(公式(12)\)消去\((\omega,b)\)可得：

\[\begin{equation}\begin{aligned} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\top} \boldsymbol{x}_{j}-\sum_{i=1}^{m} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \tag{14} \]

因此問題變成了尋找合適的\(\alpha\)使得\(公式(12)\)成立。

又因為\(公式（11）\)在極值點必定滿足KKT條件。也就是說\(\alpha_i(1-y_{i}({w}^{\top} {x}_{i}+b))=0\)，當\(\alpha_i \gt 0\)時必有\(1-y_{i}({w}^{\top} {x}_{i}+b) =0\)。因此對於\(\alpha_i \gt0\)對應的樣本是支援向量，對於非支援向量，則\(\alpha_i =0\)

對於\(公式13\)有：

\[\begin{equation}\begin{aligned} \boldsymbol{w} &=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\ &=\sum_{i: \alpha_{i}=0}^{m} 0 \cdot y_{i} \boldsymbol{x}_{i}+\sum_{i: \alpha_{i}>0}^{m} \alpha_{i} y_{i} \boldsymbol{x}_{i} \\ &=\sum_{i \in S V} \alpha_{i} y_{i} \boldsymbol{x}_{i}\quad(SV 代表所有支援向量的集合) \end{aligned}\end{equation} \]

然後我們可以求\(b\)了，對於支援向量有\(y_k =\omega^{\top}x+b\)，因此：

\[\begin{equation}\begin{aligned} b&=y_k-\boldsymbol{w}^{\top} \boldsymbol{x} \\ &=y_{k}-(\sum_{i \in S V} \alpha_{i} y_{i} \boldsymbol{x}_{i})^{\top}x_k \\ &=y_k-\sum_{i \in S V} \alpha_{i} y_{i} \boldsymbol{x}_{i}^{\top}x_k \end{aligned} \end{equation} \]

通過上面的推導，我們能夠知道支援向量機的\((\omega,b)\)僅由支援向量決定。實踐中, 為了得到對 $b \(更穩健的估計, 通常使用對所有支援向量求解得到\)b$的平均值。

綜上，我們想計算出合適的\(\omega\)和\(b\)，就必須計算出\(\alpha_i\)，然後我們就可以得到支援向量，在然後我們我們通過支援向量和\(\alpha_i\)就可以計算出\(\omega\)和\(b\)。

至於怎麼求\(\alpha_i\)，我們使用可以使用後面介紹的SMO演算法求解，首先我們來介紹一下核方法。

核技巧

在前面的討論中，我們對樣本的考慮都是線性可分的。但是實際上，大部分的情況下，資料都是非線性可分的。比如說異或問題。在前面的章節神經網路中，我們是通過使用增加一層隱層來解決這個問題，那麼對於SVM我們應該怎麼解決呢？SVM中使用核技巧（kernel trick）來解決非線性問題。

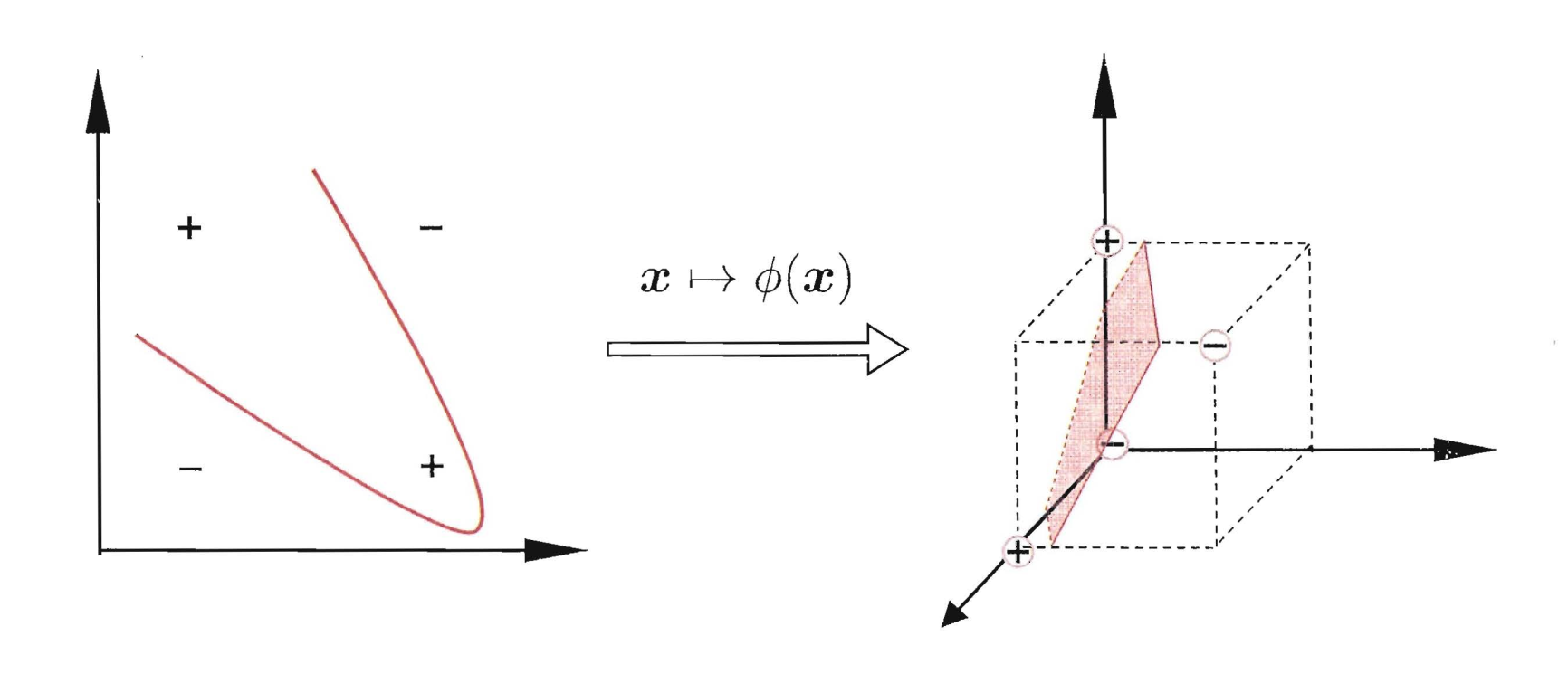
既然在原始的特徵空間\(\mathbb{R}^{d}\)不是線性可分的，支援向量機希望通過一個對映\(\phi: \mathbb{R}^{d} \rightarrow \mathbb{R}^{\tilde{d}}\), 使得資料在新的空間\(\mathbb{R}^{\tilde{d}}\)是線性可分的。可以證明（但是我證明不出），當\(d\)有限時, 一定存在\(\tilde{d}\), 使得樣本在空間$ \mathbb{R}^{\tilde{d}}$中線性可分。

核函式

令\(\phi(x)\)為\(x\)對映後的特徵向量，因此劃分的超平面可以表示為\(f(x)=\phi(x)+b\)。同時\(公式（11）\)可以改為：

\[\begin{equation}\begin{array}{l} \min _{w,b} \frac{1}{2}\|\boldsymbol{w}\|^{2} \\ \text { s.t. } y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \phi\left(\boldsymbol{x}_{i}\right)+b\right) \geqslant 1, \quad i=1,2, \ldots, m \end{array}\end{equation} \]

然後\(公式14\)可以寫成如下的形式：

\[\begin{equation}\begin{aligned} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \phi(\boldsymbol{x}_{i}^{\top}) \phi(\boldsymbol{x}_{j})-\sum_{i=1}^{m} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \tag{15} \]

求解\(公式15\)面臨一個很大的問題，那就是\(\phi(\boldsymbol{x}_{i}^{\top})\)和\(\phi(\boldsymbol{x}_{j})\)很難計算（一般來說它們都是高維的甚至無窮維），首先需要計算特徵在\(\mathbb{R}^{\tilde{d}}\)的對映，然後又要計算在他的內積，複雜度為$$\mathcal{O}(\tilde{d})$$。因此我們通過使用核技巧，將這兩步並將複雜度降低到\(\mathbb{R}^{d}\)。即核技巧希望構造一個核函式\(\kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)\)，使得：

\[\begin{equation}\kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{j}\right)\end{equation} \]

實際上核函式不僅僅只用於SVM，對於所有涉及到向量內積的運算，我們都可以使用核函式來解決。

因此\(公式15\)可以改寫成：

\[\begin{equation}\begin{aligned} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \kappa\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \tag{15} \]

對於核函式來說，我們可以自己造，但是通常我們會從一些常見的核函式中進行選擇：根據不同問題選擇不同的引數。下圖是是一些常見的核函式。

軟間隔

前面我們討論的情況都是超平面都是能夠完美的將資料進行分開（即使是非線性資料，我們使用核函式進行騷操作然後進行分割），這種所有樣本都滿足約束的情況稱之為硬間隔（hard margin），但實際上資料是有噪音的，如果使用核函式進行騷操作，然後在找到一個線性可分超平面，可能就會造成模型過擬合，同樣也可能我們找不到合適的核函式。因此，我們將標準放寬，允許一定的“錯誤”，稱之為軟間隔（soft margin）：

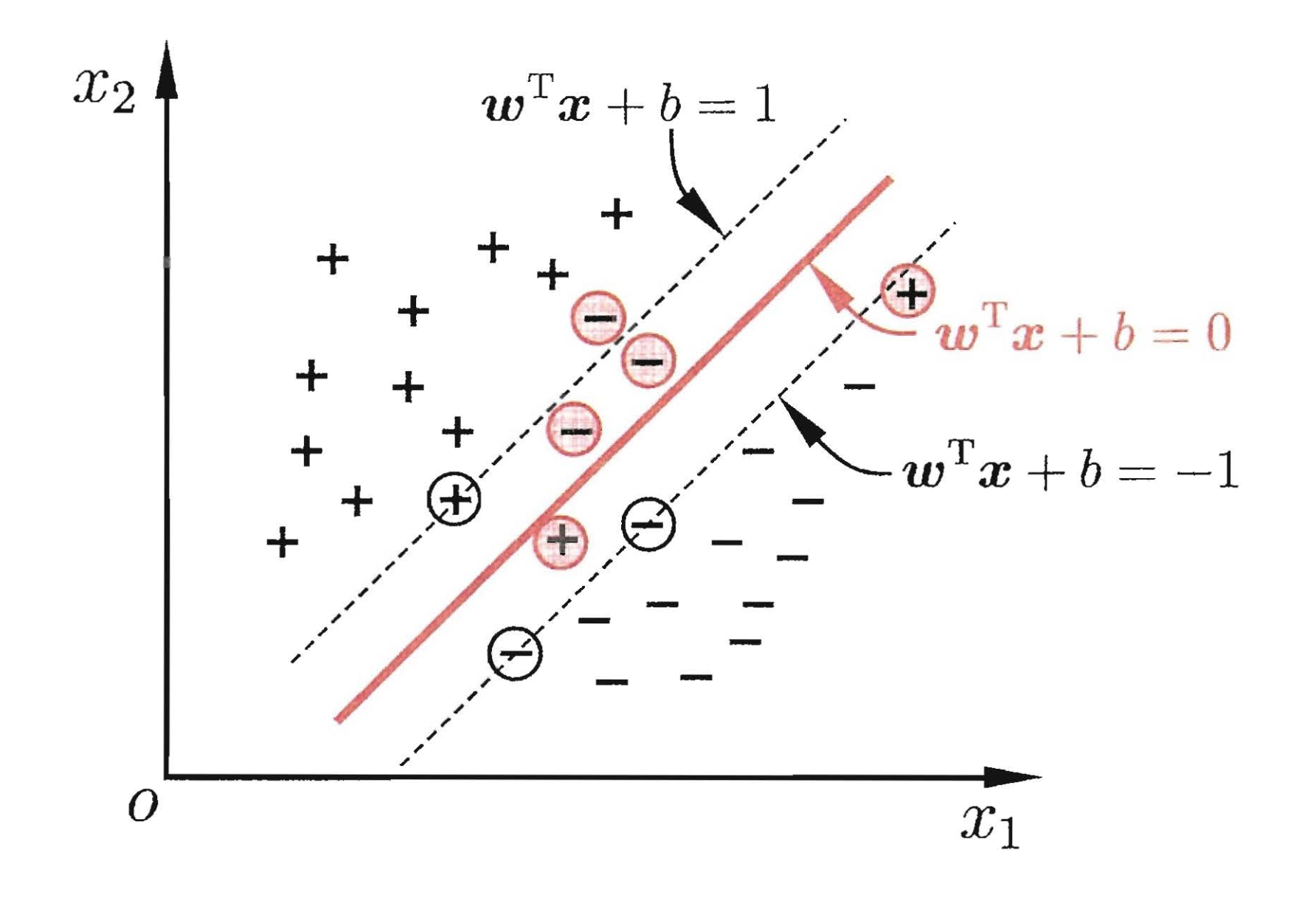
我們希望在優化間隔的同時，允許錯誤樣本的出現，但是我們同樣希望出現錯誤的樣本越少越好。因此優化目標\(公式（5）\)可寫成：

\[\left \{ \begin{matrix} \begin{align*} & min _{\boldsymbol{w}, b} \left(\frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \ell_{0 / 1}\left(y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)-1\right)\right)\\ & s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \end{align*} \end{matrix} \right. \tag{16} \]

其中\(C \gt 0\)是一個常數，\(\ell_{0 / 1}\)是“0/1損失函式”。

\[\begin{equation}\ell_{0 / 1}(z)=\left\{\begin{array}{ll} 1, & \text { if } z<0 \\ 0, & \text { otherwise } \end{array}\right.\end{equation} \]

可以很簡單的知道，\(C\)取無窮大時，\(公式（16）\)迫使所有樣本均滿足約束。當\(C\)取有限值時，允許一些樣本不滿足約束。but，還是有些問題，\(\ell_{0 / 1}\)是非凸，非連續的一個函式，會使得上式\((16)\)變得不好求解，因此人們通常使用其他的函式來替代\(\ell_{0 / 1}\)，稱之為“替代損失(surrogate loss)”。下面是幾種常用的替代損失函式：

\[\begin{equation}\begin{aligned} &\text {hinge 損失}：\ell_{\text {hinge}}(z)=\max (0,1-z) \\ &\text { 指數損失(exponential loss): } \ell_{\exp }(z)=\exp (-z)\\ &\text { 對率損失(logistic loss): } \ell_{\log }(z)=\log (1+\exp (-z)) \end{aligned}\end{equation} \]

對應的圖如下：

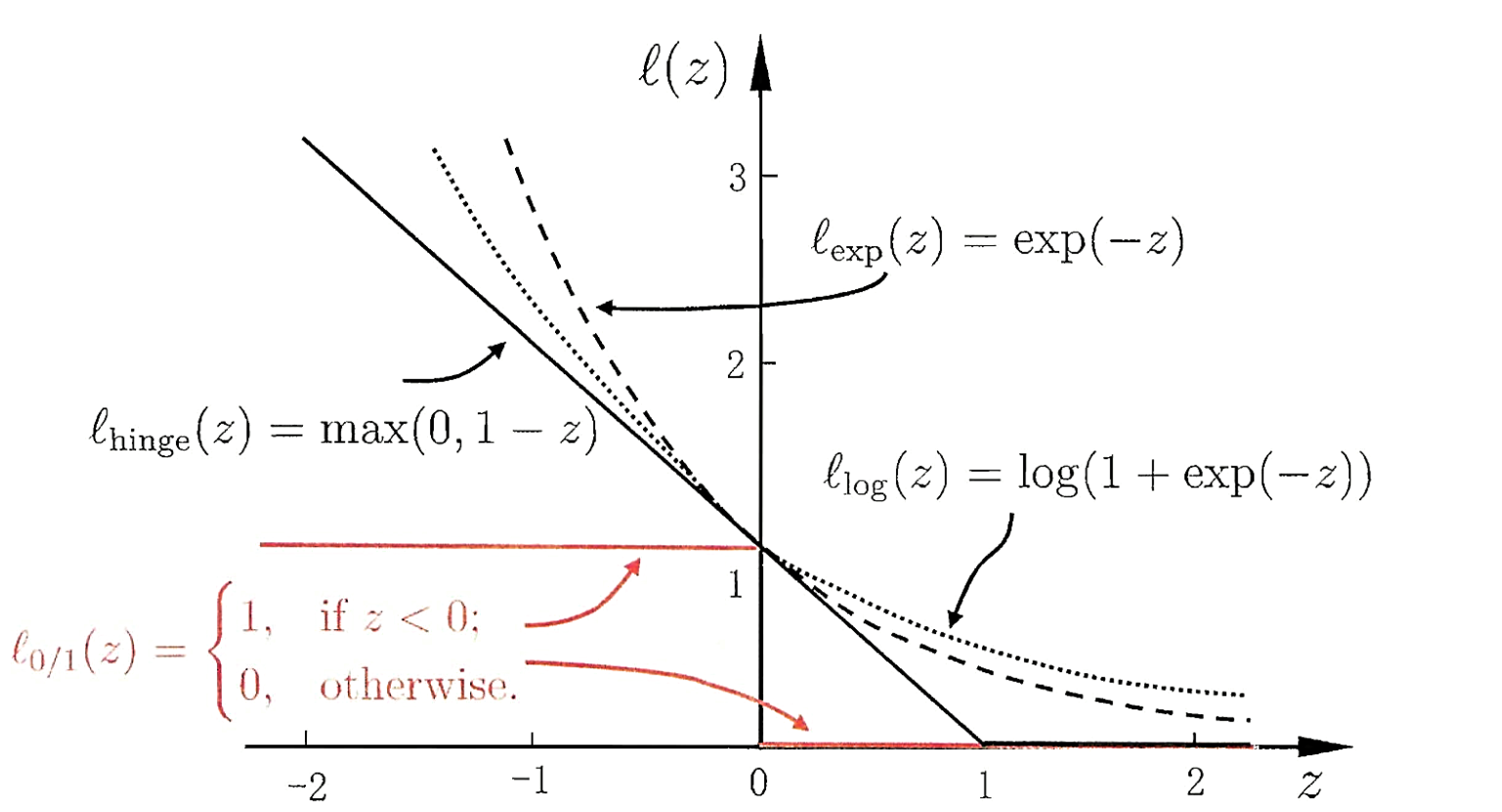
下面將以\(hinge函式\)為例子介紹軟間隔支援向量機的推導。

軟間隔支援向量機推導

\(\text {hinge函式}：\ell_{\text {hinge}}(z)=\max (0,1-z)\)等價於：

\[\begin{equation}\xi_{i}=\left\{\begin{array}{ll}0 & \text { if } y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) \geq 1 \\1-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) & \text { otherwise }\end{array}\right.\end{equation} \]

\(\xi_{i}\)我們稱之為鬆弛變數（slack variable），樣本違背約束越遠，則鬆弛變數值越大。因此優化目標式\((5)\)可以寫成：

\[\begin{equation}\begin{aligned}\min _{\boldsymbol{w}, b, \boldsymbol{\xi}} &( \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^{m} \xi_{i} )\\\text { s.t. } & y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) \geq 1-\xi_{i}, \quad i=1,2, \ldots, m \\& \xi_{i} \geq 0, \quad i=1,2, \ldots, m\end{aligned}\end{equation} \tag{17} \]

同樣在這裡\(C\)越大，代表我們希望越多的樣本滿足約束。軟間隔的拉格朗日函式為：

\[\begin{equation}\begin{aligned} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta}):=& \frac{1}{2} \boldsymbol{w}^{\top} \boldsymbol{w}+C \sum_{i=1}^{m} \xi_{i} \\ &+\sum_{i=1}^{m} \alpha_{i}\left(1-\xi_{i}-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right)\right) \\ &+\sum_{i=1}^{m} \beta_{i}\left(-\xi_{i}\right) \end{aligned}\end{equation} \tag{18} \]

其KKT條件為：

\[\begin{equation}\left\{\begin{array}{l} 1 - \xi_{i}-y_{i}\left(\boldsymbol{w}^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)+b\right) \leq 0,-\xi_{i} \leq 0 \quad(主問題可行)\\ \alpha_{i} \geq 0, \beta_{i} \geq 0 \quad(對偶問題可行)\\ \alpha_{i}\left(1-\xi_{i}-y_{i}\left(\boldsymbol{w}^{\top} \phi\left(\boldsymbol{x}_{i}\right)+b\right)\right)=0, \beta_{i} \xi_{i}=0 \quad(互補鬆弛)\\ \end{array}\right.\end{equation} \]

其對偶問題為：

\[\begin{equation}\begin{aligned} \max _{\boldsymbol{\alpha}, \boldsymbol{\beta}} \min _{\boldsymbol{w}, b, \boldsymbol{\xi}} & \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \\ \text { s.t. } & \alpha_{i} \geq 0, \quad i=1,2, \ldots, m \\ & \beta_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}\end{equation} \]

\(\min _{\boldsymbol{w}, b, \boldsymbol{\xi}} \mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\beta})\)的優化屬於無約束的優化問題，我們通過將偏導置零的方法得到\((\boldsymbol{w}, b, \boldsymbol{\xi})\)的最優值：

\[\begin{equation}\begin{aligned} \frac{\partial \mathcal{L}}{\partial \boldsymbol{w}}=\mathbf{0} & \Rightarrow \boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right) \\ \frac{\partial \mathcal{L}}{\partial b} &=0 \Rightarrow \sum_{i=1}^{m} \alpha_{i} y_{i}=0 \\ \frac{\partial \mathcal{L}}{\partial \boldsymbol{\xi}} &=\mathbf{0} \Rightarrow \alpha_{i}+\beta_{i}=C \end{aligned}\end{equation}\tag{19} \]

因為\(\beta_{i}=C -\alpha_{i} \ge0\)，因此我們約束\(0 \le \alpha_i \le C\)，將\(\beta_{i}=C -\alpha_{i},{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} \boldsymbol{\phi}\left(\boldsymbol{x}_{i}\right)\)，代入式\((18)\)可得：

\[\begin{equation}\begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} \phi\left(\boldsymbol{x}_{i}\right)^{\top} \boldsymbol{\phi}\left(\boldsymbol{x}_{j}\right)-\sum_{i=1}^{m} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{m} \alpha_{i} y_{i}=0,\\ & 0 \le \alpha_i \le C \end{array}\end{equation} \tag{20} \]

如果我們將式\((17)\)看成如下一般形式：

\[\begin{equation}\min _{f} (\Omega(f)+C \sum_{i=1}^{m} \ell\left(f\left(\boldsymbol{x}_{i}\right), y_{i}\right))\end{equation} \]

對於\(\Omega(f)\)我們稱之為“結構風險（structural risk）”，第二項\(\sum_{i=1}^{m} \ell\left(f\left(\boldsymbol{x}_{i}\right), y_{i}\right)\)稱之為“經驗分享（empirical risk）“，而\(C\)的作用就是對兩者進行折中。

SMO演算法

前面說了這麼多，終於終於，我們要開始說SMO（Sequential minimal optimization，序列最小化）演算法了。首先說一下這個演算法的目的，這個演算法就是用來求\(\alpha_i\)的。SMO演算法是一種啟發式演算法，基本思路是如果所有變數的解都滿足最優化問題的KKT條件，則該最優化問題的解就得到了。

對於式\((19)\)如果我們將\(\phi({x}_{i})^{\top} {\phi}(\boldsymbol{x}_{j})\)使用核函式來表示則有：

\[\begin{equation}\begin{aligned} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \end{aligned}\end{equation} \tag{21} \]

假如我們選擇\(\alpha_1,\alpha_2\)作為變數(至於為什麼不是隻選擇一個變數是因為存在$\sum_{i=1}^{N} \alpha_{i} y_{i}=0 \(這個約束條件)，固定其他變數\)\alpha_{i}(i=3,4, \cdots, N)\(，則式\)(20)$問題可以變成：

\[\begin{equation}\begin{array}{rl} \min _{\alpha_{1}, \alpha_{2}} & W\left(\alpha_{1}, \alpha_{2}\right)=\frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}- \\ & \left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{N} y_{i} \alpha_{i} K_{i 2} \\ \text { s.t. } & \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\varsigma \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2 \end{array}\end{equation} \tag{22} \]

在式\((21)\)中省略了\(\sum_{i=3}^N\alpha_i\)這個式子，是因為該式為常數項。

因為\(\alpha_{1} y_{1}+\alpha_{2} y_{2} = 常數，y_1 = \pm1,y_2=\pm1\)，因此有：

\[\begin{equation}\left\{\begin{array}{l} \alpha_1 - \alpha_2 = k \quad(y_1 \ne y_2)\\ \alpha_1 + \alpha_2 = k \quad(y_1 = y_2)\\ \end{array} \right. \end{equation} \quad \text { s.t. }0 \leqslant \alpha_{1} \leqslant C，0 \leqslant \alpha_{2} \leqslant C\\ \tag{23} \]

我們可以將式\((22)\)用圖表示出來：

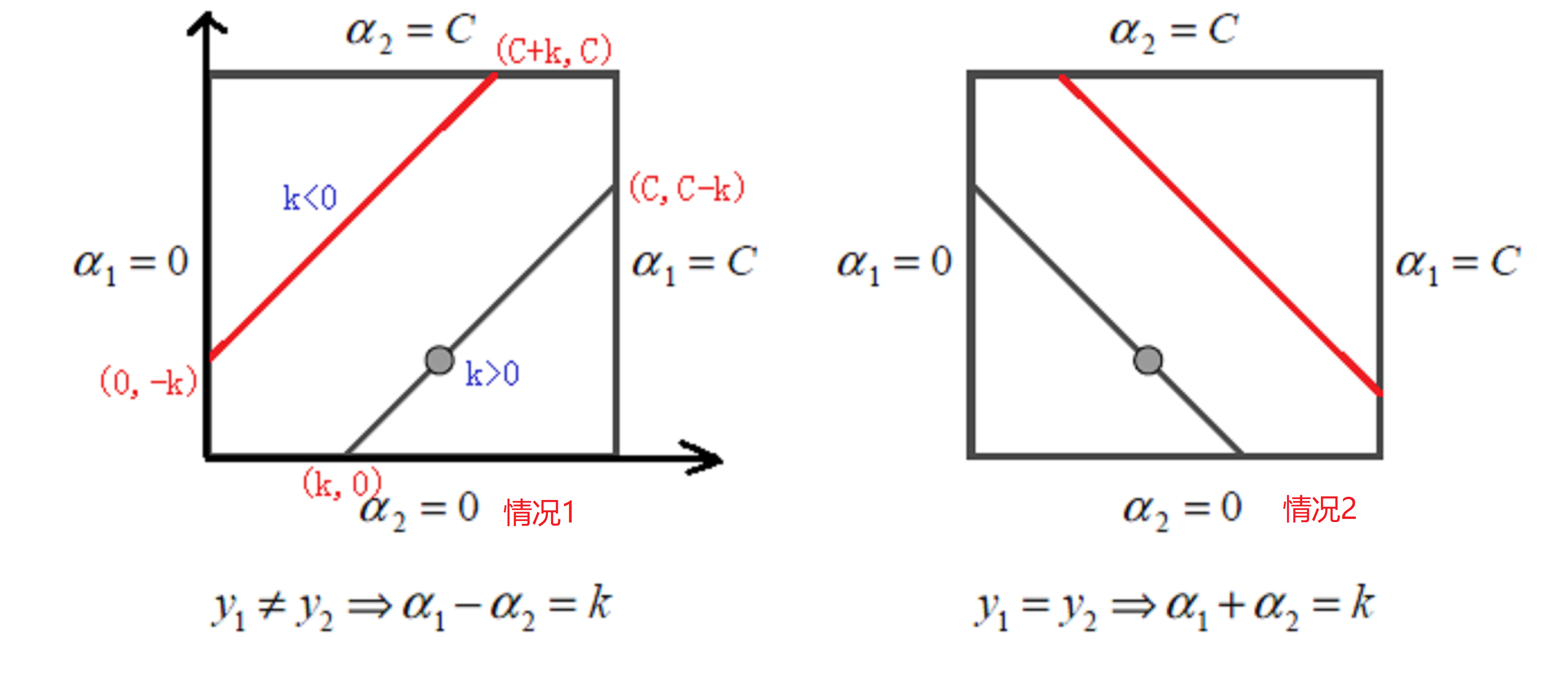
因為\(\alpha_1\)和\(\alpha_2\)存線上性關係，這樣兩個變數的最優化問題成為了實質上單變數的最優化問題，因此，我們可以看成其為變數\(\alpha_2\)的最優化問題。

設\(式(22)\)的初始可行解為\(\alpha_{1}^{\text {old }}, \alpha_{2}^{\text {old }}\)，最優解為\(\alpha_{1}^{\text {new }}, \alpha_{2}^{\text {new}}\)。對於\(\alpha_i^{new}\)來說，其取值範圍必須滿足：

\[L \leqslant \alpha_{i}^{\text {new }} \leqslant H \]

• 情況1：\(L=\max \left(0, \alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right), \quad H=\min \left(C, C+\alpha_{2}^{\text {old }}-\alpha_{1}^{\text {old }}\right)\)
• 情況2：\(L=\max \left(0, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}-C\right), \quad H=\min \left(C, \alpha_{2}^{\text {old }}+\alpha_{1}^{\text {old }}\right)\)

設我們計算出來的\(\alpha_2\)為\(\alpha_2^{new,unc}\)，則有：

\[\alpha_2^{new}= \begin{cases} H& { \alpha_2^{new,unc} > H}\\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\\ L& {\alpha_2^{new,unc} < L} \end{cases} \]

那麼問題就回到了如果我們有\(\alpha_2^{old}\)我們如何得到\(\alpha_2^{new,unc}\)呢？

首先我們設一個超平面函式\(g(x)\)如下：

\[設：g(x) = w^{*} \bullet \phi(x) + b\\ 由式（19）可知{w}=\sum_{i=1}^{m} \alpha_{i} y_{i} {\phi}({x}_{i}) \\ 因此有： g(x)=\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*} \]

然後我們令

\[\begin{equation}E_{i}=g\left(x_{i}\right)-y_{i}=\left(\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b\right)-y_{i}, \quad i=1,2\end{equation} \]

同時引進記號：

\[\begin{equation}v_{i}=\sum_{j=3}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)=g\left(x_{i}\right)-\sum_{j=1}^{2} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)-b, \quad i=1,2\end{equation} \]

因此式\((22)\)可以改寫成：

\[\begin{equation}\begin{array}{c} W\left(\alpha_{1}, \alpha_{2}\right)=| \frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}- \\ \left(\alpha_{1}+\alpha_{2}\right)+y_{1} v_{1} \alpha_{1}+y_{2} v_{2} \alpha_{2} \end{array}\end{equation} \tag{24} \]

又因為\(\alpha_{1} y_{1}+\alpha_{2} y_{2}=\varsigma,\quad y_iy_i = 1\)，因此\(\alpha_1\)可以表示為：

\[\begin{equation}\alpha_{1}=\left(\varsigma-y_{2} \alpha_{2}\right) y_{1}\end{equation} \]

代入式\((24)\)中，我們有：

\[\begin{equation}\begin{aligned} W\left(\alpha_{2}\right)=& \frac{1}{2} K_{11}\left(s-\alpha_{2} y_{2}\right)^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{2} K_{12}\left(s-\alpha_{2} y_{2}\right) \alpha_{2}-\\ &\left(s-\alpha_{2} y_{2}\right) y_{1}-\alpha_{2}+v_{1}\left(s-\alpha_{2} y_{2}\right)+y_{2} v_{2} \alpha_{2} \end{aligned}\end{equation} \]

然後，我們對\(\alpha_2\)求導數：

\[\begin{equation}\begin{aligned} \frac{\partial W}{\partial \alpha_{2}}=& K_{11} \alpha_{2}+K_{22} \alpha_{2}-2 K_{12} \alpha_{2}-\\ & K_{11 S} y_{2}+K_{12} s y_{2}+y_{1} y_{2}-1-v_{1} y_{2}+y_{2} v_{2} \end{aligned}\end{equation} \]

令其導數為0可得：

\[\begin{equation}\begin{aligned} \left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}=& y_{2}\left(y_{2}-y_{1}+\varsigma K_{11}-\varsigma K_{12}+v_{1}-v_{2}\right) \\ =& y_{2}\left[y_{2}-y_{1}+\varsigma K_{11}-\varsigma K_{12}+\left(g\left(x_{1}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{1 j}-b\right)-\right.\\ &\left.\left(g\left(x_{2}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{2 j}-b\right)\right] \end{aligned}\end{equation} \tag{25} \]

又因為\(\varsigma=\alpha_{1}^{\mathrm{old}} y_{1}+\alpha_{2}^{\mathrm{old}} y_{2}\)代入式\((25)\)可得：

\[\begin{equation}\begin{aligned} \left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {new }, \text { unc }} &=y_{2}\left(\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {old }} y_{2}+y_{2}-y_{1}+g\left(x_{1}\right)-g\left(x_{2}\right)\right) \\ &=\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text {old }}+y_{2}\left(E_{1}-E_{2}\right) \end{aligned}\end{equation} \tag{26} \]

令：

\[\begin{equation}\eta=K_{11}+K_{22}-2 K_{12}=\left\|\Phi\left(x_{1}\right)-\Phi\left(x_{2}\right)\right\|^{2}\end{equation} \]

因此式\((26)\)可化簡為：

\[\begin{equation}\alpha_{2}^{\text {new }, \mathrm{unc}}=\alpha_{2}^{\text {old }}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta}\end{equation} \tag{27} \]

同時有：

\[\alpha_2^{new}= \begin{cases} H& { \alpha_2^{new,unc} > H}\\ \alpha_2^{new,unc}& {L \leq \alpha_2^{new,unc} \leq H}\\ L& {\alpha_2^{new,unc} < L} \end{cases} \]

因為我們已經得到\(\alpha_2^{new}\)，根據\(\alpha_1^{new}\)和\(\alpha_2^{new}\)之間的線性關係，我們可以就可以得到\(\alpha_1^{new}\)了。

我們每次完成兩個變數的優化之後，都需要重新更新閾值。具體更新可以看下面部分。

SMO變數的選擇方法

通過前面部分我們知道SMO演算法就是選擇兩個變數進行優化，其中至少有一個變數是違反了KKT條件（假如沒有違反的話，我們也就沒必要進行計算了）。我們可以使用\(\alpha_1\)代表第一個變數，\(\alpha_2\)代表第二個變數。

1. 第一個變數的選擇

   我們稱第一個變數的選擇為外層迴圈，外層迴圈在訓練樣本中選擇違反KKT條件最嚴重的樣本點。對於KKT條件，我們可以轉成以下的形式：

   \[\begin{equation}\begin{aligned} \alpha_{i} &=0 \Leftrightarrow y_{i} g\left(x_{i}\right) \geqslant 1 &\quad(1)\\ 0<\alpha_{i} &<C \Leftrightarrow y_{i} g\left(x_{i}\right)=1 &\quad(2)\\ \alpha_{i} &=C \Leftrightarrow y_{i} g\left(x_{i}\right) \leqslant 1 &\quad(3)\\ 其中g(x_{i}) &= \sum_{j=1}^{N}\alpha_{j}y_{j}K(x_{i},x_{j})+b\\ \end{aligned}\end{equation} \tag{28} \]

   證明如下：

   對於上式\((1)\)：

   \[\begin{equation}\begin{aligned} &\because\alpha_i = 0,\alpha_i + \beta_i = C ,且在KKT條件\beta_{i}\xi_{i}=0\\ &\therefore \beta_i = C,\therefore\xi_i = 0\\ 又&\because 由KTT條件可知：1-\xi_i\le y_ig(x_i)，\alpha_{i} [y_{i}g(x_{i})-(1-\xi_{i})]=0\\ &\therefore y_ig(x_i) \ge 1 \end{aligned}\end{equation} \]

   對於上式\((2)\)：

   \[\begin{equation}\begin{aligned} &\because0<\alpha_{i} <C ,\alpha_i + \beta_i = C ,且在KKT條件\beta_{i}\xi_{i}=0\\ &\therefore 0 \lt\beta_i \lt C,\therefore\xi_i = 0\\ 又&\because 由KTT條件可知：1-\xi_i\le y_ig(x_i)，\alpha_{i} [y_{i}g(x_{i})-(1-\xi_{i})]=0\\ &\therefore y_ig(x_i) = 1-\xi_i = 1 \end{aligned}\end{equation} \]

   對於上式\((3)\)：

   \[\begin{equation}\begin{aligned} &\because\alpha_i = C,\alpha_i + \beta_i = C ,且在KKT條件\beta_{i}\xi_{i}=0\\ &\therefore \beta_i = 0，\xi_i \ge0\\ 又&\because 由KTT條件可知：1-\xi_i\le y_ig(x_i)，\alpha_{i} [y_{i}g(x_{i})-(1-\xi_{i})]=0\\ &\therefore y_ig(x_i) = 1-\xi_i \le 1 \end{aligned}\end{equation} \]

   當然我們也可以給定一定的精度範圍\(\varepsilon\)，此時KKT條件就變成了：

   \[\begin{equation}\begin{array}{l} a_{i}=0 \Leftrightarrow y_{i} g\left(x_{i}\right) \geq 1-\varepsilon \\ 0<a_{i}<C \Leftrightarrow 1-\varepsilon \leq y_{i} g\left(x_{i}\right) \leq 1+\varepsilon \\ a_{i}=C \Leftrightarrow y_{i} g\left(x_{i}\right) \leq 1+\varepsilon \end{array}\end{equation} \]

   然後我們通過變形後的KKT條件，獲得違背的樣本點違背最嚴重的作為第一個變數就