【cs224w】Lecture 5 - 譜聚類
阿新 • • 發佈:2020-04-07
[TOC]
轉自本人:https://blog.csdn.net/New2World/article/details/105372317
## Spectral Clustering
前面的課程說到了 community detection 並介紹了兩種演算法。這次來說說另外一類做社群聚類的演算法,譜聚類。這種演算法一般分為三個步驟
1. pre-processing: 構建一個描述圖結構的矩陣
2. decomposition: 通過特徵值和特徵向量分解矩陣
3. grouping: 基於分解後的矩陣以及點的 representation 進行聚類
在介紹具體操作前我們先了解幾個概念
### Graph Partitioning
圖的劃分就是將節點分到不同的組內,如果分為兩個組就是二分。劃分的目的其實就是找社群,那如何判斷一個劃分的質量呢?回顧之前說到的社群的特點,即社群內部連線豐富而社群間連線稀疏。因此我們希望我們的劃分能最大化每個劃分內的連線並最小化劃分間的連線數。我們用割這個概念來描述不同劃分間的連線數 $cut(A,B)=\sum\limits_{i\in A,j\in B}w_{ij}$。對於無權圖這裡的 $w$ 就是 $\{0,1\}$。但這個定義並不完美,因為這樣並不能保證劃分均勻。例如,一個圖中有一個節點的度為 $1$ 那麼只要把這個節點和其餘節點分開就能保證 cut 為 $1$。因此我們將劃分後不同組內節點的度納入考慮就能較為全面的評估一個劃分的好壞了,即 Conductance,其中 $vol$ 是劃分內所有節點的度之和。
$$\phi(A,B)=\frac{cut(A,B)}{\min(vol(A),vol(B))}$$
然而直接最小化 conductance 是個 NP-hard 的問題。那接下來就進入今天的正題:譜聚類。
首先複習一下線性代數,給定一個圖的鄰接矩陣 $A$,那 $i$ 行表示節點 $i$ 的所有出度,$j$ 列表示節點 $j$ 的所有入度。在無向圖上出度入度一樣,因此 $A^T=A$,。考慮無向圖,那 $Ax$ 代表什麼?$Ax$ 的輸出是一個向量,而向量的每一個元素是矩陣的行和向量 $x$ 的內積。如果將 $x$ 看作圖中每個節點的分類標籤,那得到的結果向量的每個元素代表了每個節點所有鄰接節點的標籤之和。 而特徵值的定義是 $Ax=\lambda x$,而譜聚類就是研究根據特徵值 $\lambda$ 升序排序後的特徵向量。(這裡規定 $\Lambda=\{\lambda_1,\lambda_2,...,\lambda_n\}$ 且 $\lambda_1\leq\lambda_2 \leq...\leq\lambda_n$) ### $d$-Regular Graph 現在給出一個特殊的連通圖 $G$,圖中所有節點的度都為 $d$。然後令 $x=(1,1,...,1)$ 那麼 $Ax=(d,d,...,d)=\lambda x$,因此 $\lambda=d$。可以證明 $d$ 是最大的特徵值。 > 證明: > 因為我們希望特徵值為 $d$,那對向量 $x$ 必須有 $x_i=x_j$。也就是說 $x=c\cdot(1,1,...,1)$ > 那麼對於任意不滿足 $c\cdot(1,1,...,1)$ 的向量 $y$,說明並非所有節點都為 $1$。令不為 $1$ 的節點集為 $S$,顯然並非所有節點都在 $S$ 中。 > 這樣一來必定存在節點 $j$,其鄰接節點不屬於 $S$。這樣一來在節點 $j$ 這裡得到的內積值必定嚴格小於 $d$ > 因此 $y$ 不是特徵向量,且 $d$ 是最大的特徵值 以上是針對連通圖。如果圖不連通而是有兩個部分,且每部分都是 $d$-regular 的。我們做類似處理,不過對 $x$ 的定義會適當改變。 $$\begin{cases} x'=(1,...,1,0,...,0)^T, Ax'=(d,...,d,0,...,0)^T \\ x''=(0,...,0,1,...,1)^T, Ax''=(0,...,0,d,...,d)^T \end{cases}$$ 這樣一來對應的特徵值仍然是 $\lambda=d$,但這個最大特徵值對應了兩個特徵向量。 > 為什麼不繼續用 $x=(1,1,...,1)^T$? > 你試試 $Ax=\lambda x$ 對得上不? 如下圖稍微推廣一下,第一種不連通情況下,最大和第二大的特徵值相等。第二種情況屬於存在明顯社群結構,此時圖其實是連通的,但最大和第二大的特徵值差別不大。而 $\lambda_{n-1}$ 能告訴我們兩個社群的劃分情況。  那為什麼說 $\lambda_{n-1}$ 能告訴我們劃分情況?首先我們知道特徵向量是互相垂直的,即兩個特徵向量的內積為 $0$。因此在已知 $x_n=(1,1,...,1)^T$ 的情況下,$x_nx_{n-1}=0$ 說明 $\sum_ix_{n-1}[i]=0$。因此,在 $x_{n=1}$ 內必定有正有負。那我們就可以依此將圖中的節點分為兩組了。(這是大致思路,還有很多細節需要考慮) 那考慮無向圖,我們定義以下幾個矩陣 1. 鄰接矩陣 $A$ - 對稱 - $n$ 個實數特徵值 - 特徵向量為實數且互相垂直 2. 度矩陣 $D$ - 對角矩陣 3. 拉普拉斯矩陣 $L=D-A$ - 半正定 - 特徵值為非負實數 - 特徵向量為實數且互相垂直 - 對所有 $x$ 有 $x^TLx=\sum_{ij}L_{ij}x_ix_j\geq 0$ 這裡有個定理:對任意對稱矩陣 $M$ 有 $$\lambda_2=\min\limits_{x:x^Tw_1=0}\frac{x^TMx}{x^Tx}$$ $w_1$ 是最小特徵值對應的特徵向量。分析一下這個表示式 $$\begin{aligned} x^TLx&=\sum\limits_{i,j=1}^nL_{ij}x_ix_j=\sum\limits_{i,j=1}^n(D_{ij}-A_{ij})x_ix_j \\ &=\sum_iD_{ii}x_i^2-\sum_{(i,j)\in E}2x_ix_j \\ &=\sum_{(i,j)\in E}(x_i^2+x_j^2-2x_ix_j) \\ &=\sum_{(i,j)\in E}(x_i-x_j)^2 \end{aligned}$$ 因為度矩陣 $D$ 是對角矩陣,所以上面才會化簡為 $D_{ii}$。 因為這裡的求和是針對每條邊,而每條邊有兩個端點,因此第三步是 $x_i^2+x_j^2$。化簡了定理裡的表示式能看出什麼?$\lambda_2$ 是特徵向量裡各元素的差的平方(距離)的最小值。這與我們找最小割目的不謀而合,即最小化各部分間的連線數。 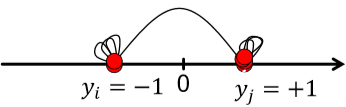 這樣得到的 $x$ 叫 Fiedler vector。然而直接用離散的標籤 $\{-1,1\}$ 太硬核了,我們考慮允許 $x$ 為滿足約束的實數。即 $\sum_ix_i=0, \sum_ix_i^2=1$ 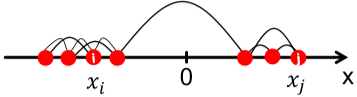 > 其實這裡偷換了概念。表示式裡應該將 $x$ 替換為 $y$。因為分析的時候我們將 $y$ 視為劃分後的標籤,而特徵值 $x_2$ 只是這個標籤 $y$ 的最優解而已。 這裡提到了 approx. guarantee,如果將網路劃分為 $A$ 和 $B$,那可以保證 $\lambda_2$ 和 conductance $\beta$ 存在關係 $\lambda_2\leq2\beta$ (證明略,自己看 slide 吧)
根據這種方法得到的結果還是不錯的。如果網路中包含了不止一個劃分,我們可以遞迴地使用上述演算法,即先劃分為兩部分,然後對兩部分分別再用使用一次或多次譜聚類。除此之外還可以使用 $x_3,x_4,...$ 等特徵向量一起進行聚類,這樣一來相當於將每個點表示為 $k$ 維的向量進行聚類。一般來說多用幾個特徵向量能避免資訊丟失,得到更好的聚類結果。那這個 $k$ 怎麼選呢?看 $\Delta_k=|\lambda_k-\lambda_{k-1}|$。選令 eigengap 最大的 $k$ 就好。(注意!!這裡的特徵值又是按**降序**排列的了)[^1] 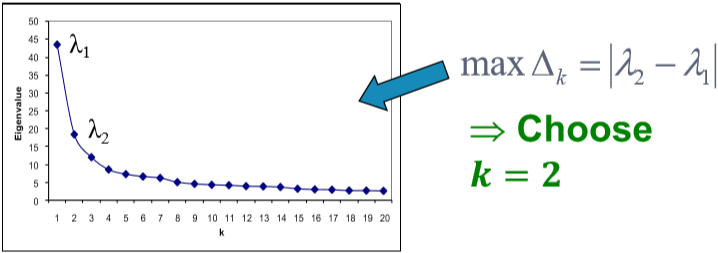 ## Motif-Based Spectral Clustering 上面的譜聚類是基於邊實現的,如果我們想針對某種特定的結構進行劃分呢?自然而然的想到之前介紹的 motif。基於 motif 也就是說在一個劃分內特定的 motif 普遍出現。類似對邊的劃分,我們定義 $vol_M(S)$ 為在劃分 $S$ 裡的 motif 的端點個數,$\phi(S)=\frac{\#(motifs\ cut)}{vol_M(S)}$。當然這也是 NP-hard 的。 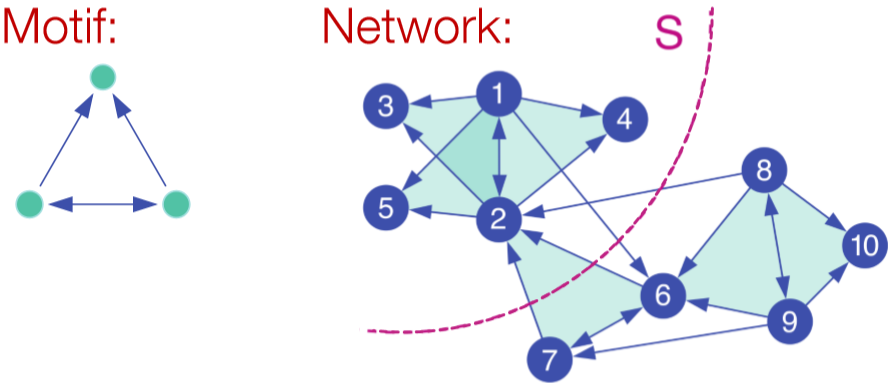 走流程,首先我們需要定義矩陣 $W^{(M)}$。這裡矩陣內每個元素代表了對應邊被幾個 motif 共享。然後是度矩陣 $D^{(M)}=\sum_jW_{ij}^{(M)}$ 和拉普拉斯矩陣 $L^{(M)}=D^{(M)}-W^{(M)}$。求特徵值和特徵向量後取第二小的特徵值對應的特徵向量 $x_2$。按升序對 $x_2$ 各元素大小排序,並依次通過計算 motif conductance 來找最佳的劃分。(前 $k$ 小的元素為 $x_2^{(1)},x_2^{(2)},...,x_2^{(k)}$,然後計算 conductance。取令 conductance 最小的 $k$ 值)[^2] 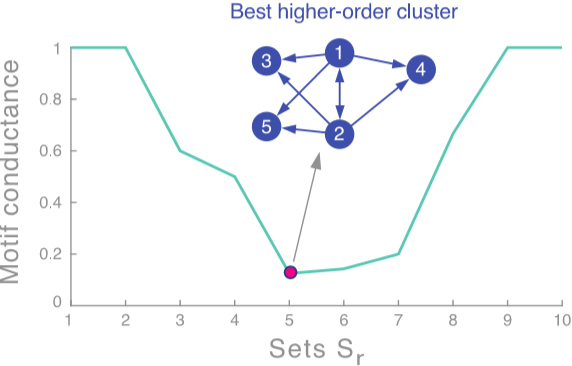 當然這個演算法也只是一個近似,它能保證 $\phi_M(S)\leq4\sqrt{\phi_M^*}$ [^1]: 雖然選最大的 gap 是 make sense 的。但要說個所以然還是有點講不清楚,需要再理解理解。 [^2]: 這個方法叫 sweep procedure,不同於之前以 $0$ 為界的劃分。那 motif-based 能用之前的方法嗎?sweep procedure 有什麼優勢嗎?基於邊的譜聚類能用 sweep procedur
首先複習一下線性代數,給定一個圖的鄰接矩陣 $A$,那 $i$ 行表示節點 $i$ 的所有出度,$j$ 列表示節點 $j$ 的所有入度。在無向圖上出度入度一樣,因此 $A^T=A$,。考慮無向圖,那 $Ax$ 代表什麼?$Ax$ 的輸出是一個向量,而向量的每一個元素是矩陣的行和向量 $x$ 的內積。如果將 $x$ 看作圖中每個節點的分類標籤,那得到的結果向量的每個元素代表了每個節點所有鄰接節點的標籤之和。 而特徵值的定義是 $Ax=\lambda x$,而譜聚類就是研究根據特徵值 $\lambda$ 升序排序後的特徵向量。(這裡規定 $\Lambda=\{\lambda_1,\lambda_2,...,\lambda_n\}$ 且 $\lambda_1\leq\lambda_2 \leq...\leq\lambda_n$) ### $d$-Regular Graph 現在給出一個特殊的連通圖 $G$,圖中所有節點的度都為 $d$。然後令 $x=(1,1,...,1)$ 那麼 $Ax=(d,d,...,d)=\lambda x$,因此 $\lambda=d$。可以證明 $d$ 是最大的特徵值。 > 證明: > 因為我們希望特徵值為 $d$,那對向量 $x$ 必須有 $x_i=x_j$。也就是說 $x=c\cdot(1,1,...,1)$ > 那麼對於任意不滿足 $c\cdot(1,1,...,1)$ 的向量 $y$,說明並非所有節點都為 $1$。令不為 $1$ 的節點集為 $S$,顯然並非所有節點都在 $S$ 中。 > 這樣一來必定存在節點 $j$,其鄰接節點不屬於 $S$。這樣一來在節點 $j$ 這裡得到的內積值必定嚴格小於 $d$ > 因此 $y$ 不是特徵向量,且 $d$ 是最大的特徵值 以上是針對連通圖。如果圖不連通而是有兩個部分,且每部分都是 $d$-regular 的。我們做類似處理,不過對 $x$ 的定義會適當改變。 $$\begin{cases} x'=(1,...,1,0,...,0)^T, Ax'=(d,...,d,0,...,0)^T \\ x''=(0,...,0,1,...,1)^T, Ax''=(0,...,0,d,...,d)^T \end{cases}$$ 這樣一來對應的特徵值仍然是 $\lambda=d$,但這個最大特徵值對應了兩個特徵向量。 > 為什麼不繼續用 $x=(1,1,...,1)^T$? > 你試試 $Ax=\lambda x$ 對得上不? 如下圖稍微推廣一下,第一種不連通情況下,最大和第二大的特徵值相等。第二種情況屬於存在明顯社群結構,此時圖其實是連通的,但最大和第二大的特徵值差別不大。而 $\lambda_{n-1}$ 能告訴我們兩個社群的劃分情況。  那為什麼說 $\lambda_{n-1}$ 能告訴我們劃分情況?首先我們知道特徵向量是互相垂直的,即兩個特徵向量的內積為 $0$。因此在已知 $x_n=(1,1,...,1)^T$ 的情況下,$x_nx_{n-1}=0$ 說明 $\sum_ix_{n-1}[i]=0$。因此,在 $x_{n=1}$ 內必定有正有負。那我們就可以依此將圖中的節點分為兩組了。(這是大致思路,還有很多細節需要考慮) 那考慮無向圖,我們定義以下幾個矩陣 1. 鄰接矩陣 $A$ - 對稱 - $n$ 個實數特徵值 - 特徵向量為實數且互相垂直 2. 度矩陣 $D$ - 對角矩陣 3. 拉普拉斯矩陣 $L=D-A$ - 半正定 - 特徵值為非負實數 - 特徵向量為實數且互相垂直 - 對所有 $x$ 有 $x^TLx=\sum_{ij}L_{ij}x_ix_j\geq 0$ 這裡有個定理:對任意對稱矩陣 $M$ 有 $$\lambda_2=\min\limits_{x:x^Tw_1=0}\frac{x^TMx}{x^Tx}$$ $w_1$ 是最小特徵值對應的特徵向量。分析一下這個表示式 $$\begin{aligned} x^TLx&=\sum\limits_{i,j=1}^nL_{ij}x_ix_j=\sum\limits_{i,j=1}^n(D_{ij}-A_{ij})x_ix_j \\ &=\sum_iD_{ii}x_i^2-\sum_{(i,j)\in E}2x_ix_j \\ &=\sum_{(i,j)\in E}(x_i^2+x_j^2-2x_ix_j) \\ &=\sum_{(i,j)\in E}(x_i-x_j)^2 \end{aligned}$$ 因為度矩陣 $D$ 是對角矩陣,所以上面才會化簡為 $D_{ii}$。 因為這裡的求和是針對每條邊,而每條邊有兩個端點,因此第三步是 $x_i^2+x_j^2$。化簡了定理裡的表示式能看出什麼?$\lambda_2$ 是特徵向量裡各元素的差的平方(距離)的最小值。這與我們找最小割目的不謀而合,即最小化各部分間的連線數。  這樣得到的 $x$ 叫 Fiedler vector。然而直接用離散的標籤 $\{-1,1\}$ 太硬核了,我們考慮允許 $x$ 為滿足約束的實數。即 $\sum_ix_i=0, \sum_ix_i^2=1$  > 其實這裡偷換了概念。表示式裡應該將 $x$ 替換為 $y$。因為分析的時候我們將 $y$ 視為劃分後的標籤,而特徵值 $x_2$ 只是這個標籤 $y$ 的最優解而已。 這裡提到了 approx. guarantee,如果將網路劃分為 $A$ 和 $B$,那可以保證 $\lambda_2$ 和 conductance $\beta$ 存在關係 $\lambda_2\leq2\beta$ (證明略,自己看 slide 吧)
根據這種方法得到的結果還是不錯的。如果網路中包含了不止一個劃分,我們可以遞迴地使用上述演算法,即先劃分為兩部分,然後對兩部分分別再用使用一次或多次譜聚類。除此之外還可以使用 $x_3,x_4,...$ 等特徵向量一起進行聚類,這樣一來相當於將每個點表示為 $k$ 維的向量進行聚類。一般來說多用幾個特徵向量能避免資訊丟失,得到更好的聚類結果。那這個 $k$ 怎麼選呢?看 $\Delta_k=|\lambda_k-\lambda_{k-1}|$。選令 eigengap 最大的 $k$ 就好。(注意!!這裡的特徵值又是按**降序**排列的了)[^1]  ## Motif-Based Spectral Clustering 上面的譜聚類是基於邊實現的,如果我們想針對某種特定的結構進行劃分呢?自然而然的想到之前介紹的 motif。基於 motif 也就是說在一個劃分內特定的 motif 普遍出現。類似對邊的劃分,我們定義 $vol_M(S)$ 為在劃分 $S$ 裡的 motif 的端點個數,$\phi(S)=\frac{\#(motifs\ cut)}{vol_M(S)}$。當然這也是 NP-hard 的。  走流程,首先我們需要定義矩陣 $W^{(M)}$。這裡矩陣內每個元素代表了對應邊被幾個 motif 共享。然後是度矩陣 $D^{(M)}=\sum_jW_{ij}^{(M)}$ 和拉普拉斯矩陣 $L^{(M)}=D^{(M)}-W^{(M)}$。求特徵值和特徵向量後取第二小的特徵值對應的特徵向量 $x_2$。按升序對 $x_2$ 各元素大小排序,並依次通過計算 motif conductance 來找最佳的劃分。(前 $k$ 小的元素為 $x_2^{(1)},x_2^{(2)},...,x_2^{(k)}$,然後計算 conductance。取令 conductance 最小的 $k$ 值)[^2]  當然這個演算法也只是一個近似,它能保證 $\phi_M(S)\leq4\sqrt{\phi_M^*}$ [^1]: 雖然選最大的 gap 是 make sense 的。但要說個所以然還是有點講不清楚,需要再理解理解。 [^2]: 這個方法叫 sweep procedure,不同於之前以 $0$ 為界的劃分。那 motif-based 能用之前的方法嗎?sweep procedure 有什麼優勢嗎?基於邊的譜聚類能用 sweep procedur
