• Node Classification
  • Probabilistic Relational Classifier
  • Iterative Classification
  • Belief Propagation

轉自本人：https://blog.csdn.net/New2World/article/details/105410276

前面幾課時講的主要是圖的性質、一些基本結構和針對結構的演算法。而從現在開始就要涉及到具體的 learning 任務了。這一講要解決的主要問題是：給定一個網路以及網路裡一部分節點的標籤，我們如何為其它節點分類。(semi-supervised)
我們使用的模型叫 collective classification model，其中有三種近似推斷的方法，它們都是迭代型演算法。

• relational classification
• iterative classification
• belief propagation

exact inference vs. approximate inference
例如在一個圖裡每個節點都是離散的隨機變數，而所有節點的類別的聯合分佈為 \(p\)。那麼我們要得到某個節點的類別的分佈就是求 \(p\) 在該節點上的邊沿分佈。而邊沿分佈需要累加其它所有節點，這個計算量爆炸，因此需要近似推斷。
近似推斷其實就是縮小傳播範圍的過程，與其考慮所有節點，我們只關心目標節點的鄰接點。這裡涉及到資訊傳遞，就是類似 GNN 裡的 aggregation，後面會說到。

Node Classification

給節點分類，我們的第一想法是節點間通過邊的連線存在著相關性，那我們直接通過相關性對節點進行分類。關聯性主要有三種

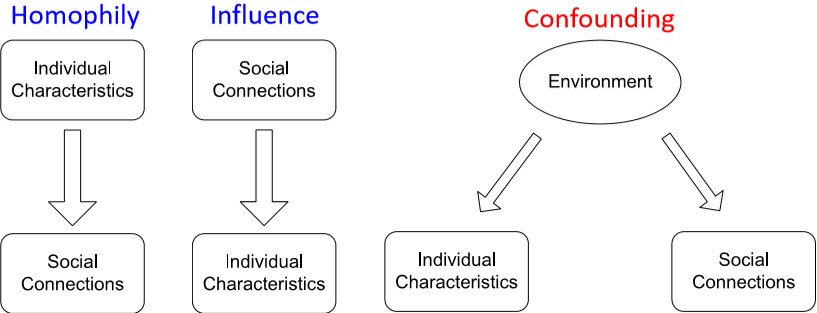
• homophily：“物以類聚，人以群分”，有相同性質的節點間可能存在更密切的聯絡
• influence：“近朱者赤，近墨者黑”，一個個體有可能會受其它個體的影響而具有某種性質
• confounding：大環境可能會對個體性質和個體間的聯絡產生影響

那麼將這種關聯性的特點應用在節點分類裡，相似的節點間一般會有直接的聯絡，互相連線的點很有可能屬於同一類別，這就是 guilt-by-association (關聯推斷)。而節點類別的判斷可以基於節點的特徵以及鄰接節點的類別和特徵。
由於做的是近似推斷，所以這裡需要做出馬爾可夫假設，即節點 \(i\) 的類別 \(Y_i\) 只取決於它的鄰接節點 \(N_i\)。因此有 \(P(Y_i|i)=P(Y_i|N_i)\)

Collective classification 大體分為三步：

1. local classifier：就像一般的分類任務一樣，只依賴節點自己的特徵資訊而不牽扯任何網路資訊
2. relational classifier：考慮鄰接點的標籤和特徵
3. collective inference：迭代地將 relational classifier 應用在每個節點上，相當於拓展了節點的“感知野”

Probabilistic Relational Classifier

基本思路很簡單，每個節點類別的概率是其鄰接節點的加權平均。
首先將有標籤的點的類別初始化為標籤，沒有標籤的點初始化為隨機。然後按隨機順序進行鄰接節點類別加權，直到整個網路收斂或達到最大迭代次數。但這樣做有兩個問題，第一不保證收斂；其次這樣的模型並沒有用到節點的特徵。

Iterative Classification

其實就是加上節點特徵後的迭代過程。(1) Bootstrap phase，通過訓練集訓練兩個分類器，一個針對節點本身的特徵，一個針對節點和網路連線特徵 (資料來自其它網路)，比如 SVM 什麼的。然後對每個節點提取特徵並用第一個分類器來初始化標籤。因為分類器並沒有考慮網路資訊，因此還需要 (2) Iteration phase 對網路中的關聯進行迭代，即使用第二個分類器每個節點根據其鄰接點更新特徵和標籤，直到收斂或達到最大迭代次數。然而這個方法依然無法保證收斂。
slide 裡給了一個用 word-bag 作為特徵的網頁分類的例子，感興趣可以去看看。

接下來是一個 iterative classification 的應用，對 fake reviewer/review 進行分類。它將 reviewer 和網頁作為二分圖處理，雖然也可以加上 reviewer 間的關係，但那樣做會破壞這個方法的兩個優點：(1) 迭代次數有上界；(2) 時間複雜度和邊的條數成線性。
論文裡給 reviewer，review 和網頁都定義了 quality score。然後大致按照上面講的方法對這些值進行迭代更新。

• reviewer: \(F(u)=\frac{\sum\limits_{(u,p)\in Out(u)}R(u,p)}{|Out(u)|}\)
• review: \(R(u,p)=\frac1{\gamma_1+\gamma_2}(\gamma_1F(u)+\gamma_2(1-\frac{|score(u,p)-G(p)|}2))\)
• 網頁: \(G(p)=\frac{\sum\limits_{(u,p)\in In(p)}R(u,p)\cdot score(u,p)}{|In(p)|}\)

有學生問到一個問題：如果一個人對所有網頁都給 good review，那他算不算 fake？
Michele 的回答是這樣做只會讓這個人的評分趨近 \(0.5\) 而不會像那種給好網頁評負分的真正的 fake reviewer 那樣得分趨近 \(0\)
另一個有意思的問題是，如果某個人口味獨特，給某些奇怪的網站評了高分，會不會被認為是 fake？
我很好奇口味有多獨特，奇怪的網頁指什麼。但實際上世界很大，網路規模也很大，有獨特癖好的不止你一個，因此你不孤單。總有那麼一群人給這些奇怪的網頁評高分，相對來說也就不會被分為 fake。不過這個問題也得看實際情況。

Belief Propagation

信念傳播是一個動態規劃的過程，主要用於解決圖模型中的條件概率問題。不過在看它到底是什麼東西前我們先了解下資訊傳遞是怎麼回事。想象一群高度近視的人不戴眼鏡在操場上排了個縱隊，他們只能看到前面和後面一個人。這種情況下如何讓他們知道自己在第幾個？很簡單，第一個人告訴第二個人“你前面有一個人(就是第一個人自己)”，第二個人告訴第三個人“你前面倆人”，依次類推所有人都知道自己第幾了。同理，如果從最後一個人開始往前，那麼就能知道隊伍的總人數了(正數和倒數第幾都有了)。這個道理用到網路裡其實差不多，每個節點能知道自己的大概位置。但是一旦遇到環，這個方法就沒完了……這個我們待會兒再說。該介紹信念傳播的演算法了：Loopy Belief Propagation

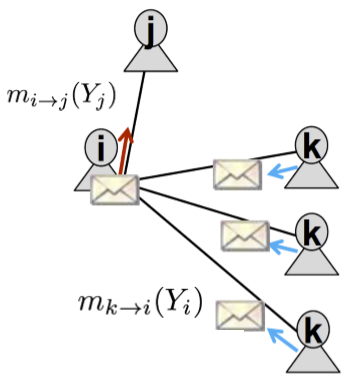
在上圖的簡單網路結構中，節點 \(i\) 發給 \(j\) 的資訊包含了節點 \(k\) 發給 \(i\) 的資訊。因此先做如下定義

• label-label potential matrix \(\psi(Y_i,Y_j)\)：表示節點 \(i\) 是類別 \(Y_i\) 的條件下，其鄰接節點 \(j\) 為類別 \(Y_j\) 的概率
• prior belief \(\phi_i(Y_i)\)：表示節點 \(i\) 為類別 \(Y_i\) 的先驗概率
• \(m_{i\rightarrow j}(Y_j)\)：節點 \(i\) 在多大程度上認為其鄰接節點 \(j\) 是類別 \(Y_j\) (不知道這裡能不能算作是一個概率)

這個式子應該很好理解：節點 \(i\) 為 \(Y_i\) 時，有個先驗 \(\phi\)，同時它會收到節點 \(k\) 的資訊 \(m_{k\rightarrow i}(Y_i)\)，然後根據類似轉移矩陣的 \(\psi\) 得到節點 \(j\)。這裡的 \(\alpha\) 類似於學習率。
老規矩，隨機順序迭代，直到收斂，然後就得到了節點 \(i\) 是類別 \(Y_i\) 的信念。

好，信念傳播的過程和模型介紹了，需要來解決環的問題了。在傳播過程中，環的存在可能會導致信念的重複累加，但這樣對結果不會造成太大影響，因為它無非就是讓節點更加確信結果而已。其最主要的問題是可能會導致原本相關的資訊被作為獨立資訊來處理，如下圖中圈出的兩個資訊。這兩條資訊其實是同一條，但因為信念傳播是區域性演算法，因此它會將這兩條資訊作為相互獨立的兩條資訊來對待。那我們怎麼解決呢？我沒理解錯的話 Michele 的意思是不用處理……因為這個例子很極端，而實際中環的影響很弱，比如有些環很~長，而大多數環存在至少一種弱相關性^[1]。

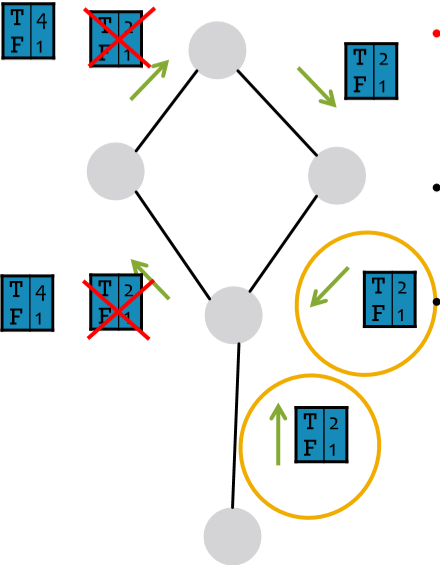
圖裡那兩個 T4F1 應該是 T4F2

核心演算法已經講了，後面還舉了個栗子，自己看 slide 吧。