CF1292C Xenon's Attack on the Gangs
阿新 • • 發佈:2020-04-11
題目連結:https://codeforces.com/problemset/problem/1292/C
題意
在一顆有n個節點的樹上,給每個邊賦值,所有的值都在\([0,n-2]\)內並且不重複,也就是一條邊一個權值,令\(mex(u,v)\)表示從\(u到v\)這條簡單路徑上沒有出現過的最小自然數,要求使所有路徑的\(mex\)之和最大。
分析
最開始我一看這個題,統計答案的時候好像就需要\(O(N^2)\),那這個題好像統計個答案就可能會T?當我看見時限是\(3s\)的時候我就知道我想多了,分析時間複雜度的時候提前看一下時限,防止因看錯時限分析錯時間複雜度。
首先這個邊的權值肯定有規律,不然列舉權值時間複雜度會很高,最開始我想的是從每個邊開始\(dfs\)一下把經過次數最多的邊設成0,然後依次類推,每次\(dfs\)不訪問重複經過的點,發現存在一個什麼問題呢,就是從不同的點開始\(dfs\)造成的結果不一樣,所以這樣不可行,不妨先畫一條鏈來看看。

如果已經放好了\(0~x-1\),考慮\(x\)放哪個位置,如果我把\(x\)放到\(5-v\)上,那麼\(mex(u,5)\)就會是\(x\),然後只有\(mex(u,v)\)會等於\(x+1\),但要是把\(x\)放到\(u-1\)或\(4-5\)上,\(mex\)等於\(x+1\)的就不會只是\(mex(u,v)\)了。鏈上是這樣,樹上當然也是,所以\(x\)放到鏈的兩端會使結果更優。
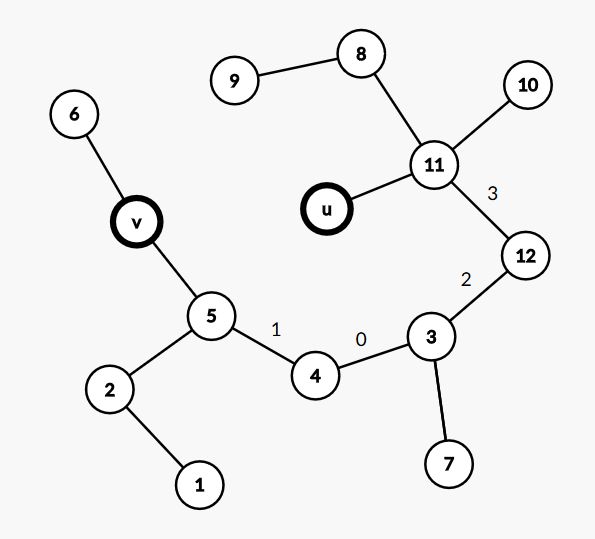
也就是這樣,對於\(u-v\)的路徑,4和5放在最兩端時結果會更優,然後對最大值5的位置進行分類討論,就可以求解出答案。
還有一個問題,如果我真的去把每個\(mex\)相加,的確很不現實,根據之前做過的一些類似的題,直接加上\(x\)相當於在\(0~x-1\)各加1,轉化成對答案的貢獻,也就是\(size_u*size_v\),這樣求解起來就會相對簡單。
之前已經講過,從不同的點開始\(dfs\)的結果是不同的,所以不能像平常那樣統計\(size\),而是應該在加一維表示根,這樣才能保證得到我們想要的\(size\),因為要列舉最大權值所在的地方,所以還要記錄每個節點的父親,同樣也要記錄根。
不妨用\(dp_{u,v}\)表示把\(0~x-1\)放到\(u-v\)的最大答案,\(s_{u,v}\)表示\(v\)以\(u\)為根時的子樹大小,\(fa_{u,v}\)表示\(v\)以\(u\)為根時的父親。於是有
\[dp_{u,v}=max(dp_{fa_{u,v},u},dp_{fa_{v,u},v})+s_{u,v}*s_{v,u} \]
然後此題就能得解,注意開long long
#include<iostream>
#define ll long long
using namespace std;
const int N=3e3+10;
struct Edge{
int to,nxt;
}e[N<<1];
int Head[N],len;
void Ins(int a,int b){
e[++len].to=b;e[len].nxt=Head[a];Head[a]=len;
}
int rt;ll s[N][N],dp[N][N],f[N][N];
void dfs(int u){
s[rt][u]=1;
for(int i=Head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==f[rt][u])continue;
f[rt][v]=u;
dfs(v);
s[rt][u]+=s[rt][v];
}
}
ll calc(int u,int v){
if(u==v)return 0;
if(dp[u][v])return dp[u][v];
return (dp[u][v]=max(calc(f[u][v],u),calc(f[v][u],v))+s[u][v]*s[v][u]);
}
int main(){
int n;
cin>>n;
for(int i=1;i<n;i++){
int a,b;
cin>>a>>b;
Ins(a,b);Ins(b,a);
}
for(int i=1;i<=n;i++)rt=i,dfs(i);
ll ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ans=max(ans,calc(i,j));
cout<<ans;
}
